Презентация на тему Колебательный контур дифференциального уравнения

содержащую соединённые катушку индуктивности и конденсатор. В такой цепи

могут возбуждаться колебания тока (и напряжения).
- простейшая система, в которой могут происходить свободные электромагнитные колебания
- это своего рода «электрический маятник»— основа многих радиотехнических устройств

системе в начале колебательного движения (электрической системе - колебательном

контуре - через создание начального заряда на обкладках конденсатора).

Пример собственные колебания - звучание колокола, гонга, струны рояля и т.п.

диф. ур-я собственных колебаний в контуре

контуре R =0. Поэтому полная энергия W остается постоянной

в течение всего времени колебаний:




где q и I — мгновенные значения заряда конденсатора и силы тока в контуре.

(так как W=const) Следовательно,





Но значит , Поэтому

диф. ур-я собственных колебаний в контуре

тогда





уравнение свободных электромагнитных колебаний в идеальном колебательном контуре

диф. ур-я собственных колебаний в контуре

значение заряда, сообщенного конденсатору; w — собственная циклическая частота

свободных электромагнитных колебаний в контуре

диф. ур-я собственных колебаний в контуре

— формула Томсона (период свободных электромагнитных колебаний в контуре).
диф.

ур-я собственных колебаний в контуре

ур-я собственных колебаний в контуре

амплитудное значение

силы тока. Следовательно, сила тока I в колебательном контуре совершает также гармонические колебания с той же частотой w, но по фазе они смещены на π/2
относительно колебаний заряда

диф. ур-я собственных колебаний в контуре

активным сопротивлением:
:

сопротивления обеспечивает потери электромагнитной энергии в контуре, что ведет

к затуханию колебаний.

Дифференциальное уравнение свободных затухающих колебаний заряда в контуре (при R≠0) , как известно

Затухающие электрические колебания

коэффициент затухания равным



дифференциальное уравнение колебаний заряда Q (см.

раздел "Свободные гармонические колебания в колебательном контуре") можно записать в аналогичном уравнению виде

Затухающие электрические колебания

декремент затухания)
Затухающие электрические колебания

δ период затухающих колебании увеличивается и при δ=ω0 равен

бесконечности, т. е. движение перестает быть периодическим. В этом случае колеблющаяся величина асимптотически стремится к нулю, когда t→∞. Данный процесс не будет колебательным. Он называется апериодическим.

Затухающие электрические колебания

незатухающими. Для этого необходимо восполнять каким-либо образом потери энергии

реальной колебательной системы.

Особенно важны и широко используются так называемые автоколебания — незатухающие колебания, которые поддерживаются в диссипативной системе за счет постоянного внешнего источника энергии, причем свойства этих колебаний задаются самой системой.

Затухающие электрические колебания

происходят без действия сил, а также от вынужденных колебаний,

которые происходят под действием периодической силы.

Автоколебательная система сама управляет внешними воздействиями, обеспечивая согласованность поступления энергии определенными порциями в нужный момент времени (в такт с ее колебаниями).

Затухающие электрические колебания

паровые турбины, двигатели внутреннего сгорания, ламповый генератор и т.

д.

Затухающие электрические колебания

совершаются не самостоятельно, а под действием периодической внешней силы.

Например, электрические колебания в антенне приемника не являются свободными, так как они происходят под воздействием приходящих радиоволн.

частотой. Будем качать его рукой с другой частотой. Характер

этого колебания зависит от движения руки и может быть, в частности, синусоидальным. К маятнику периодически подводится энергия извне; поэтому его колебания будут незатухающими и могут иметь любую частоту, которая определяется частотой внешней силы.

Вынужденные колебания

соединенном с генератором переменного тока. При любой частоте генератора

через контур проходит переменный ток, т.е. в контуре происходят вынужденные электрические колебания с частотой генератора

Вынужденные колебания

со свободными колебаниями: 1). Они являются незатухающими (вернее они существуют

в течение всего времени действия внешней эдс); 2). Они могут иметь различную форму в зависимости от характера эдс; 3). Частота их не зависит от L (индуктивность) и С (емкость) контура, а определяется частотой воздействующей эдс; 4). Амплитуда их зависит не только от величины воздействующей эдс, но и от соотношения между частотой этой эдс и собственной частотой самого контура.

Вынужденные колебания

должно быть рассмотрено подробно. В каждом колебательном контуре, получившем запас

энергии, совершаются свободные колебания с определенной собственной частотой. При малом затухании даже небольшой начальный запас энергии дает довольно продолжительные колебания. А для поддержания вынужденных колебаний на контур должна действовать периодическая внешняя эдс. Это воздействие должно быть тем сильнее, чем больше различаются между собой частота внешней эдс и частота контура.

Вынужденные колебания

вынужденных колебаний и для их поддержания требуется меньше энергии.

Если частота внешней эдс равна собственной частоте контура, то амплитуда колебаний становится максимальной и для поддержания колебаний достаточно незначительной энергии. Этот случай и называется резонансом.

Вынужденные колебания

частоты воздействующей эдс и собственной частоты контура амплитуда вынужденных

колебаний достигает наибольшей величины.

Резонанс напряжений

контура с меньшим затуханием кривая резонанса острее и выше

(рис.1 6). Это значит, что контур почти не отзывается на колебания с частотами, отличающимися от его собственной частоты, но зато при резонансе в нем возникают колебания большой амплитуды (острый резонанс). Наоборот, при большом затухании амплитуда колебаний при резонансе получается малой и.контур отзывается на колебания с частотой, значительно отличающейся от резонансной (тупой резонанс).

Резонанс напряжений

больше чувствительность контура к колебаниям резонансной частоты. Для резонанса характерно

получение мощных колебаний при небольшой затрате энергии внешнего источника, нужной только для компенсации потерь энергии при колебаниях.

Резонанс напряжений

колебаний f, и пусть внутри него работает генератор переменного

тока такой же частоты f.
1. В начальный момент конденсатор контура разряжен, генератор не работает. После включения напряжение на генераторе начинает возрастать, заряжая конденсатор. Катушка в первое мгновение не пропускает ток из-за ЭДС самоиндукции. Напряжение на генераторе достигает максимума, заряжая до такого же напряжения конденсатор

Резонанс напряжений

нем падает с такой же скоростью, с какой уменьшается

напряжение на генераторе.

3. конденсатор разряжен до нуля, вся энергия электрического поля, имевшаяся в конденсаторе, перешла в энергию магнитного поля катушки. На клеммах генератора в этот момент напряжение нулевое

Резонанс напряжений

стационарно, оно начинает уменьшаться, пересекая витки катушки в обратном

направлении. На выводах катушки появляется ЭДС индукции, которое начинает перезаряжать конденсатор. В цепи колебательного контура течет ток, только уже противоположно току заряда, так как витки пересекаются полем в обратном направлении. Обкладки конденсатора перезаряжаются зарядами, противоположными первоначальным. Одновременно растет напряжение на генераторе противоположного знака, причем с той же скоростью, с какой катушка заряжает конденсатор.

Резонанс напряжений

на генераторе к этому моменту тоже достигло максимального.
Резонанс напряжений

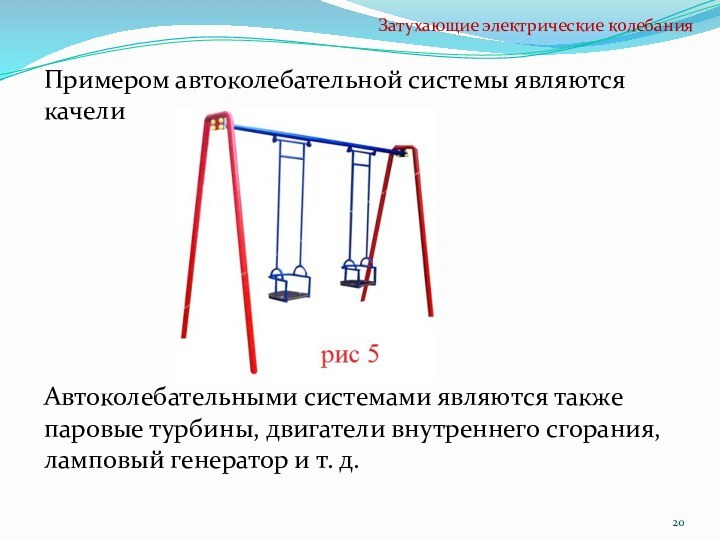
и на обоих напряжение, равное напряжению генератора. При последовательном

соединении источников питания их напряжения складываются.
Следовательно, в следующем полупериоде на катушку пойдет удвоенное напряжение (и от генератора, и от конденсатора), и колебания в контуре будут происходить при удвоенном напряжении на катушке.
В контурах с низкой добротностью напряжение на катушке будет ниже удвоенного, так как часть энергии будет рассеиваться (на излучение, на нагрев) и энергия конденсатора не перейдет полностью в энергию катушки). Соединены как бы последовательно генератор и часть конденсатора

Резонанс напряжений