- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Основи теорії механізмів і машин. (Розділ 3)
Содержание
- 2. Тема 1. Вступна лекціяПлан:1. Вступ. Основні поняття та визначення.2. Класифікація кінематичних пар.3. Ступінь рухомості механізмів.
- 3. Література: Артоболевский Н.Н., Эдельштейн Б.В. Сборник задач
- 4. 1. Вступ. Основні поняття статикиТеорія механізмів і
- 5. Машина – комплекс механізмів, які відтворюють заданий
- 6. В залежності від характеру руху ланки мають
- 7. 2. Класифікація кінематичних пар1. За видами елементів
- 8. а)
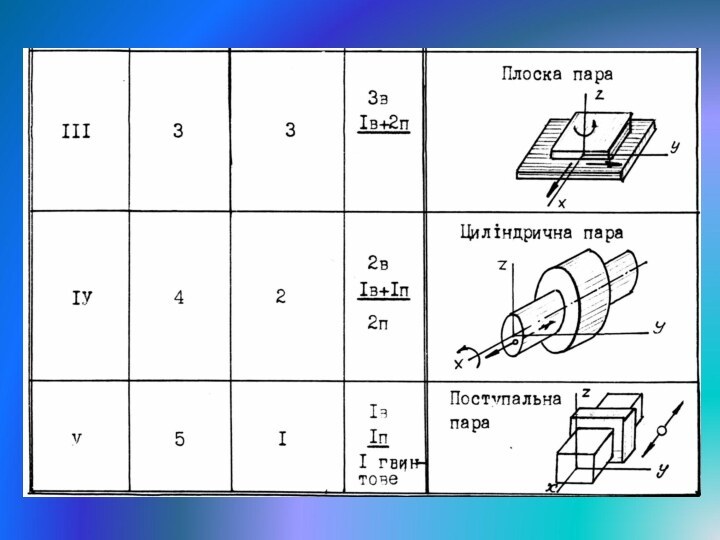
- 9. Таблиця 3.1. Класифікація кінематичних пар за кількістю ступенів вільності
- 11. 3. Ступінь рухомості механізмівСтупінь рухомості просторового механізму
- 12. Приклади. Визначити ступінь рухомості механізмів, наведених на
- 13. Контрольні питання1. Що вивчає наука “Теорія механізмів
- 14. Тема 2. Структурний аналіз стержневих механізмівПлан:Розкладання механізму
- 15. 1. Розкладання механізму на структурні групи АссураЗгідно
- 16. Групи Ассура поділяються на класи в залежності
- 17. На рис. 3.4, е – структурна група
- 18. 2. Заміна вищих кінематичних пар нижчимиПриклад заміни
- 19. в)
- 20. д)
- 21. Контрольні питання1. У чому полягає структурний аналіз
- 22. Тема 3. Кінематичний аналіз механізмівПлан:Мета та методи
- 23. 1. Мета та методи кінематичного аналізу механізмівРух
- 24. Найбільш розповсюдженими є два перших (за переліком)
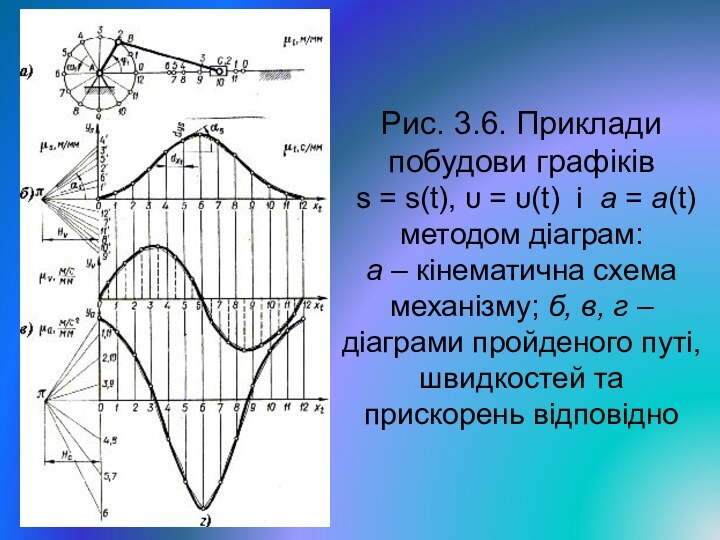
- 25. Рис. 3.6. Приклади побудови графіків s =
- 26. Скачать презентацию
- 27. Похожие презентации
Тема 1. Вступна лекціяПлан:1. Вступ. Основні поняття та визначення.2. Класифікація кінематичних пар.3. Ступінь рухомості механізмів.

















Слайд 3
Література:
Артоболевский Н.Н., Эдельштейн Б.В. Сборник задач по
теории механизмов и машин. – М.: Наука, 1975.- 256
с.Прикладная механика / Путята Т.В., Мошаровский М.С., Соколов Н.Г. и др., - Киев: Вища шк., 1977 – 536 с.
Ключові слова: механізм, машина, ланка, кінематична пара, кінематичний ланцюг, ступінь рухомості механізму, вищі та нижчі кінематичні пари.
Слайд 4
1. Вступ. Основні поняття статики
Теорія механізмів і машин
являє собою один із важливих розділів курсу “Прикладна механіка”.
Це наука про загальні методи дослідження властивостей механізмів і машин та проектування їх схем. Дослідження механізмів і машин – це вивчення руху ланок та їх точок. Побудова або синтез механізмів являє розробку раціональних методів визначення параметрів механізмів і машин за заданими функціями їх руху.Механізм – механічна система, яка призначена для отримання потрібного руху одного або кількох тіл. Головне призначення механізма – здійснення технологічних операцій.
Слайд 5 Машина – комплекс механізмів, які відтворюють заданий рух
для зміни форми тіла, його положення і т.ін.
Машини, в
яких усі перетворення енергії (матеріалів та інформації) відбуваються без безпосередньої участі людини, називаються машинами-автоматами.Ланка – одне чи декілька жорстко з’єднаних між собою твердих тіл (деталей).
В механізмі є вхідна і вихідна ланки. Ланка, якій надається рух від двигуна, називається вхідною. Ланка, яка з’єднана з робочим органом машини і змінює вхідний рух в потрібний вихідний, називається вихідною.
Слайд 6 В залежності від характеру руху ланки мають свою
назву: кривошип; коромисло; шатун; повзун; куліса; кулачок; зубчасте колесо.
Кінематична
пара (КП) – з’єднання двох ланок, що дотикаються і обмежують рух одна одної.Кінематичний ланцюг – система з’єднаних ланок, що створюють між собою КП.
Слайд 7
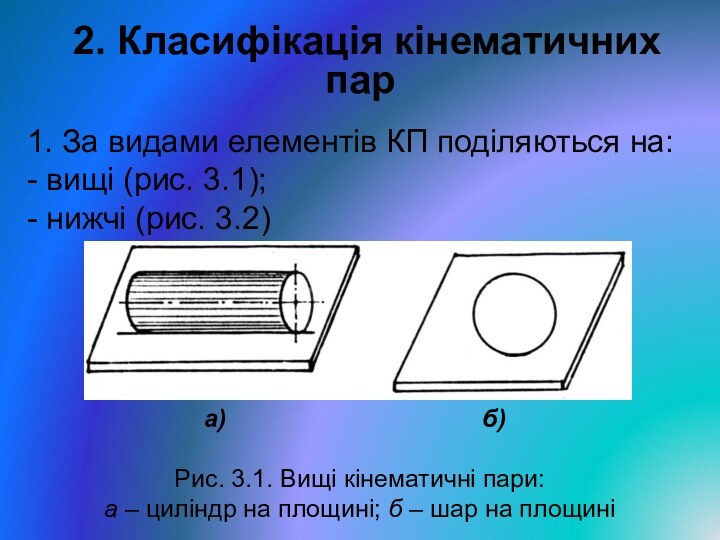
2. Класифікація кінематичних пар
1. За видами елементів КП
поділяються на:
- вищі (рис. 3.1);
- нижчі (рис. 3.2)
а) б)Рис. 3.1. Вищі кінематичні пари:
а – циліндр на площині; б – шар на площині
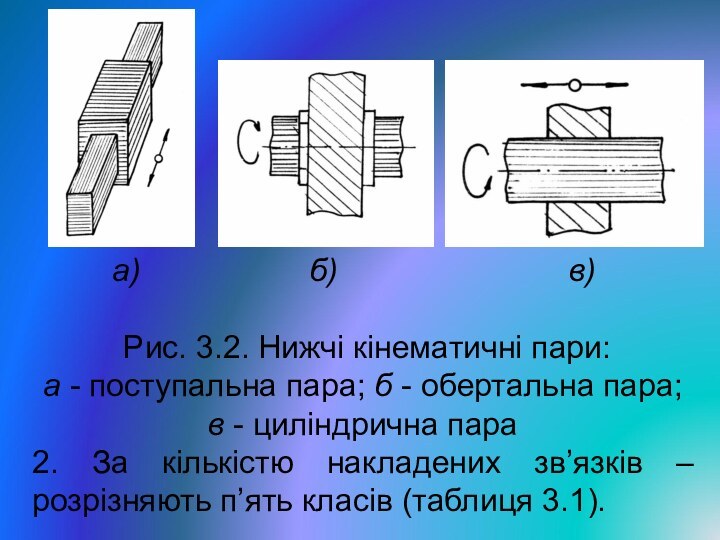
Слайд 8 а)
б)
в)Рис. 3.2. Нижчі кінематичні пари:
а - поступальна пара; б - обертальна пара; в - циліндрична пара
2. За кількістю накладених зв’язків – розрізняють п’ять класів (таблиця 3.1).
Слайд 11
3. Ступінь рухомості механізмів
Ступінь рухомості просторового механізму визначається
за формулою Малишева:
W = 6n – 5P5 – 4P4
– 3P3 – 2P5 – P1 – 6.Ступінь рухомості плоского механізму визначається за формулою Чебишева:
W = 3n – 2P5 – P4 – 3.
де n – число ланок;
P5, P4, P3, P2 – число КП 5-го, 4-го, 3-го і 2-го класів відповідно.
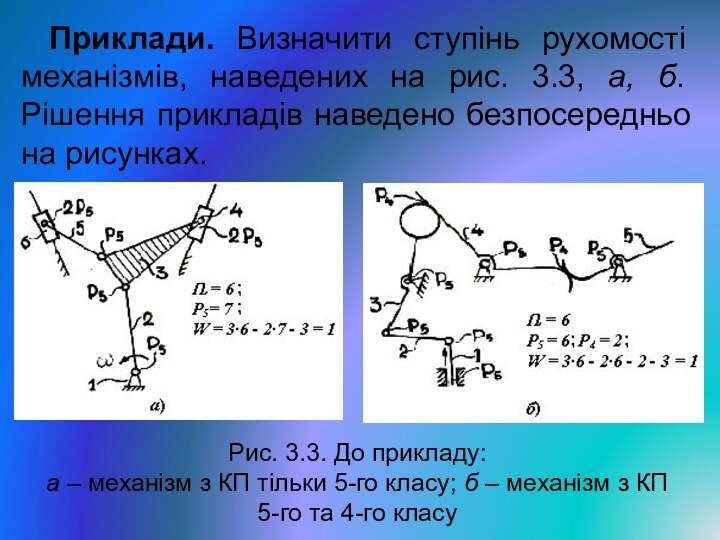
Слайд 12 Приклади. Визначити ступінь рухомості механізмів, наведених на рис.
3.3, а, б. Рішення прикладів наведено безпосередньо на рисунках.
Рис.
3.3. До прикладу:а – механізм з КП тільки 5-го класу; б – механізм з КП
5-го та 4-го класу
Слайд 13
Контрольні питання
1. Що вивчає наука “Теорія механізмів і
машин”?
2. Дайте визначення понять “механізм“, “машина“; яке призначення мають
механізми і машини?3. Що таке ланка, кінематична пара, кінематичний ланцюг?
4. Наведіть класифікацію кінематичних пар.
5. За якою формулою визначається ступінь рухомості просторового та плоского механізмів?
6. Наведіть приклади кінематичних пар 5-го і 4-го класів.
Слайд 14
Тема 2. Структурний аналіз стержневих механізмів
План:
Розкладання механізму на
структурні групи Ассура.
Заміна вищих кінематичних пар нижчими.
Ключові слова: збігальна
система сил, многокутник сил, проекція сили на вісь, умови рівноваги сил.
Слайд 15
1. Розкладання механізму на структурні групи Ассура
Згідно теорії
Ассура і Артоболевского механізм розглядається як складна система, що
складається з початкового механізму та структурних груп (груп Ассура).Початковий механізм ‑ ведуча ланка та стояк.
Структурна група Ассура – кінематичний ланцюг, який отримує нульову рухомість після приєднання його елементами зовнішніх кінематичних пар до стояка.
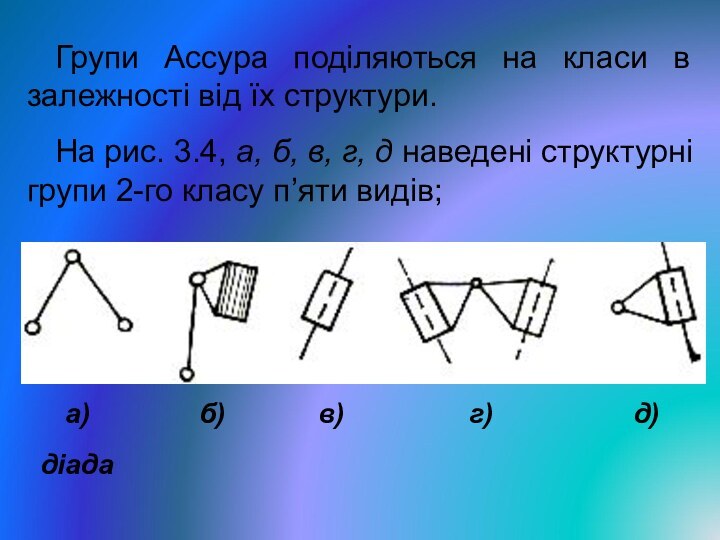
Слайд 16 Групи Ассура поділяються на класи в залежності від
їх структури.
На рис. 3.4, а, б, в, г,
д наведені структурні групи 2-го класу п’яти видів; а) б) в) г) д)
діада
Слайд 17
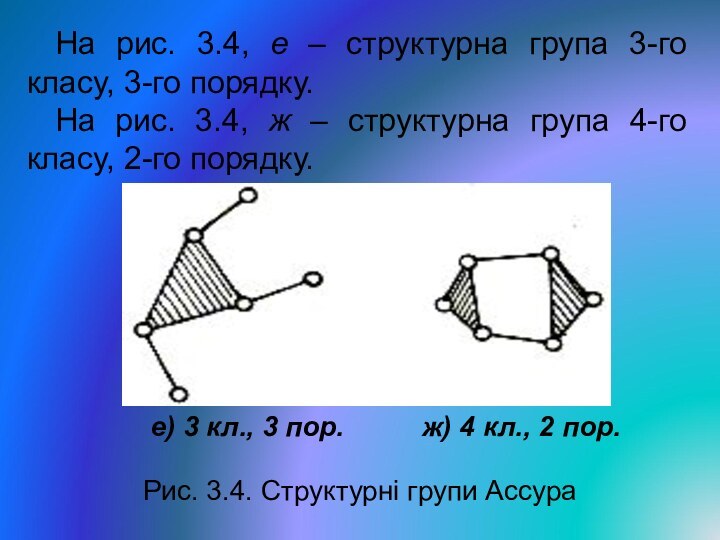
На рис. 3.4, е – структурна група 3-го
класу, 3-го порядку.
На рис. 3.4, ж – структурна група
4-го класу, 2-го порядку. е) 3 кл., 3 пор. ж) 4 кл., 2 пор.
Рис. 3.4. Структурні групи Ассура
Слайд 18
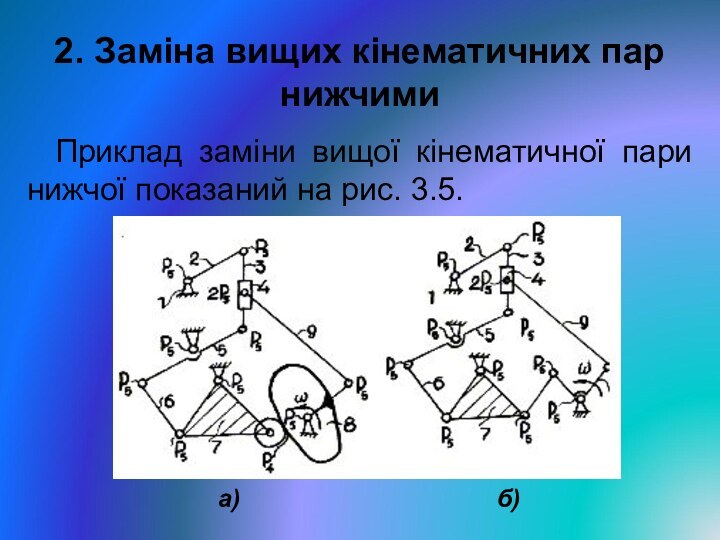
2. Заміна вищих кінематичних пар нижчими
Приклад заміни вищої
кінематичної пари нижчої показаний на рис. 3.5.
а) б)
Слайд 20
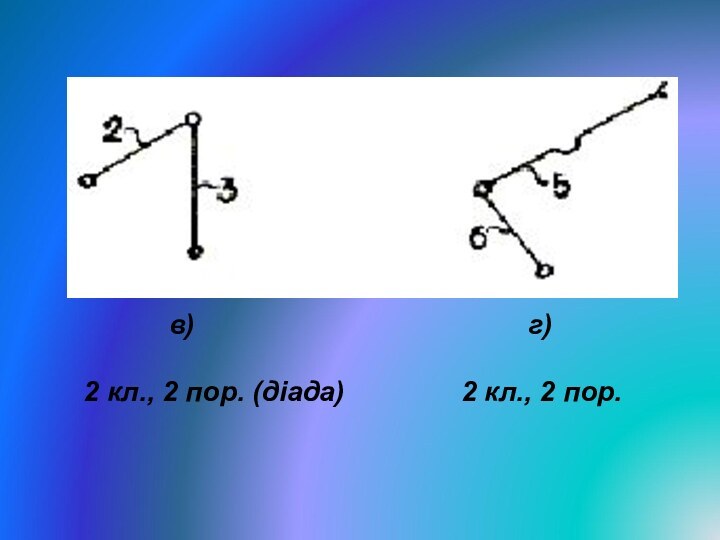
д)
е) ж)
2 кл., 2 пор. 2 кл., 1 пор. 1 кл., 2 пор.
Рис. 3.5. Заміна вищої кінематичної пари нижчою: а – заданий механізм; б – замінювальний механізм; в, г, д, е – структурні групи Ассура; ж – початковий механізм
Слайд 21
Контрольні питання
1. У чому полягає структурний аналіз механізмів?
2.
Дайте визначення початкового механізму, структурної групи Ассура.
3. Наведіть структурну
формулу групи Ассура.4. Наведіть приклади структурних груп 2-го, 3-го і 4-го класів.
5. У чому полягає заміна вищих кінематичних пар нижчими? Наведіть приклади.
Слайд 22
Тема 3. Кінематичний аналіз механізмів
План:
Мета та методи кінематичного
аналізу механізмів.
Побудова плану швидкостей.
Побудова плану прискорень.
Ключові слова: методи кінематичного
аналізу, плани швидкостей та прискорень, кутові швидкості та прискорення.
Слайд 23
1. Мета та методи кінематичного аналізу механізмів
Рух реальних
механізмів і машин відбувається під дією різних сил та
є змінним у часі відповідно до змін режимів руху машин. Кінцевою метою дослідження механізмів є визначення можливих режимів їх руху, для чого необхідно визначити переміщення, швидкості і прискорення руху ланок та їх окремих точок.Методи кінематичного аналізу механізмів: графічний метод, метод діаграм, аналітичний метод.
Слайд 24
Найбільш розповсюдженими є два перших (за переліком) методи.
Графічний
метод полягає у побудові планів швидкостей і прискорень механізму
в будь – якому його положенні.Побудова планів швидкостей і прискорень наведена у методичній розробці [2].
Метод діаграм полягає в побудові графіка S = S(t) для будь-якої точки з подальшим його графічним диференцію-ванням. У результаті отримуємо графіки зміни швидкості і прискорення у часі, тобто υ = υ (t) і а = а(t).





























