Слайд 2
Тонкостенные оболочки и пластины являются основой корпусов аппаратов
и машин разнообразного технологического назначения:
емкостного оборудования для хранения, транспортирования,
проведения химических реакций или процессов тепло- и массообмена с участием сыпучих, жидких и газообразных компонентов;
медленно вращающихся барабанов мельниц, смесителей, сушилок, печей, кристаллизаторов и фильтров;
быстроходных барабанов центрифуг, сепараторов, массообменных роторных аппаратов и т.п..
Именно эти узлы определяют надежность перечисленных и многих других аппаратов и машин в целом, и поэтому требуют подробного рассмотрения особенностей их расчета на прочность и другие главные критерии работоспособности.
Слайд 3
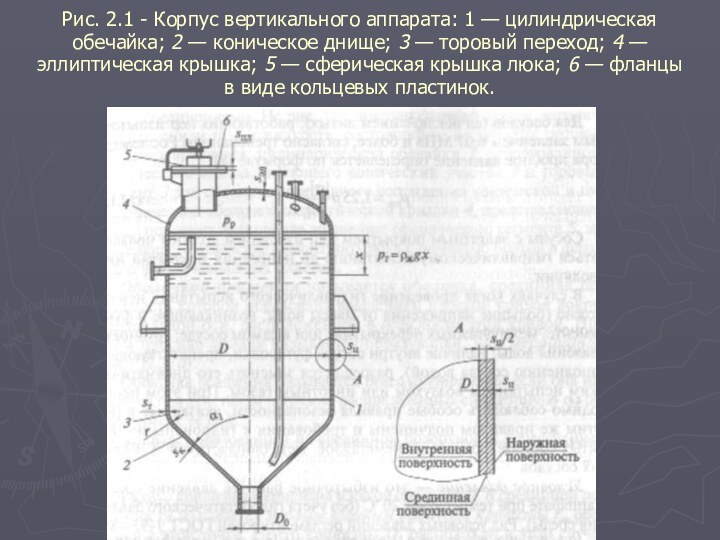
Рис. 2.1 - Корпус вертикального аппарата: 1 —
цилиндрическая обечайка; 2 — коническое днище; 3 — торовый
переход; 4 — эллиптическая крышка; 5 — сферическая крышка люка; 6 — фланцы в виде кольцевых пластинок.
Слайд 4
2.1 Общие сведения о пластинках и оболочках —
типовых элементах корпуса
Упругой оболочкой или пластинкой называется упругое тело,
одно из измерений которого (толщина) мало по сравнению с двумя другими. Если тело искривлено, оно называется оболочкой, если плоское — то пластинкой.
Условная срединная поверхность пластинки или оболочки находится на равных расстояниях от внутренней и наружной поверхности (см. рис. 2.1).
Оболочкой вращения называется такая оболочка, срединная поверхность которой образована вращением плоской кривой вокруг центральной оси, лежащей в плоскости этой кривой. Эта кривая называется образующей или меридианом (рис. 2.2). Оболочка вращения называется осесимметричной, если она находится под действием нагрузок, распределенных симметрично по отношению к ее оси.
Слайд 5
Расчетные формы и их классификация
Оболочкой называется элемент произвольной
формы, длина и ширина которого во много раз превышает
его толщину.
Оболочки могут иметь цилиндрическую, коническую или сферическую форму.
Оболочка, срединная поверхность которой представляет собой плоскость, называется пластинкой.
Встречаются пластинки прямоугольные и круглые.
Слайд 6
Кривая, образованная на срединной поверхности пересечением ее плоскостью,
перпендикулярной оси оболочки, называется параллелью (кольцом).
Радиус кривизны меридиана в
какой-либо точке срединной поверхности называется первым главным радиусом кривизны rт оболочки в этой точке. Центр кривизны 01 лежит в этом случае в осевой плоскости, соответствующей данному меридиану (см. рис. 2.2,а).
Второй главный радиус кривизны rt является образующей конуса см. рис. 2.2,6), вершина которого 02 лежит на оси вращения, а боковая поверхность перпендикулярна к срединной поверх-
ности и пересекается
с ней по параллели.
Слайд 7
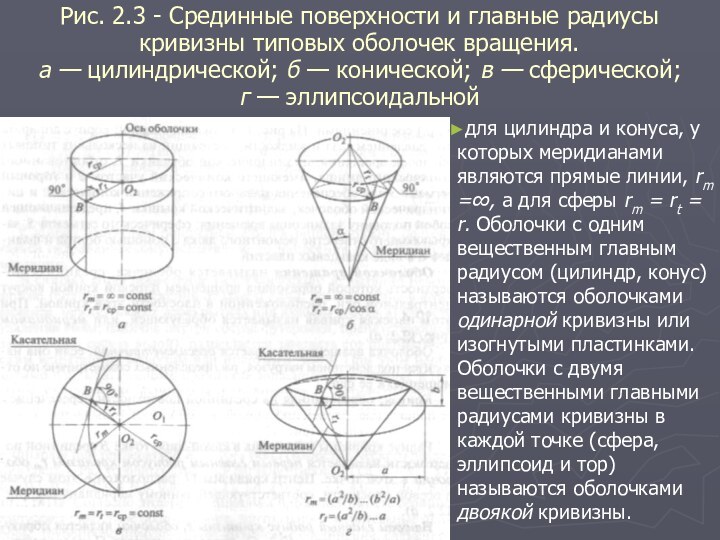
Рис. 2.3 - Срединные поверхности и главные радиусы
кривизны типовых оболочек вращения.
а — цилиндрической; б —
конической; в — сферической; г — эллипсоидальной
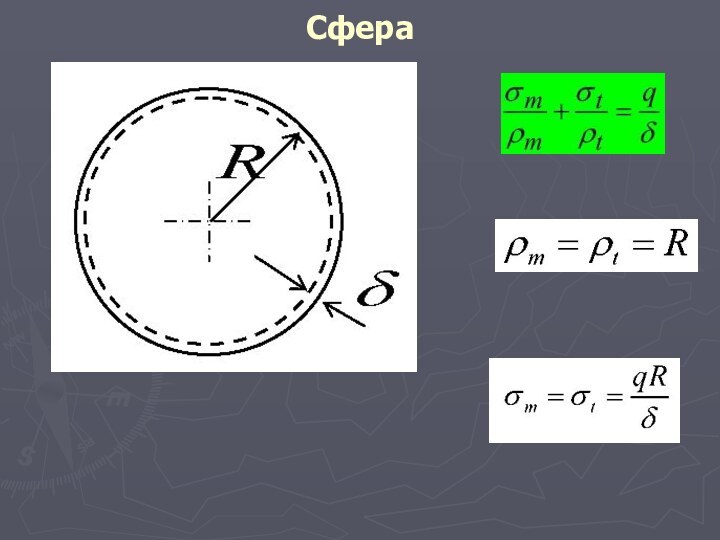
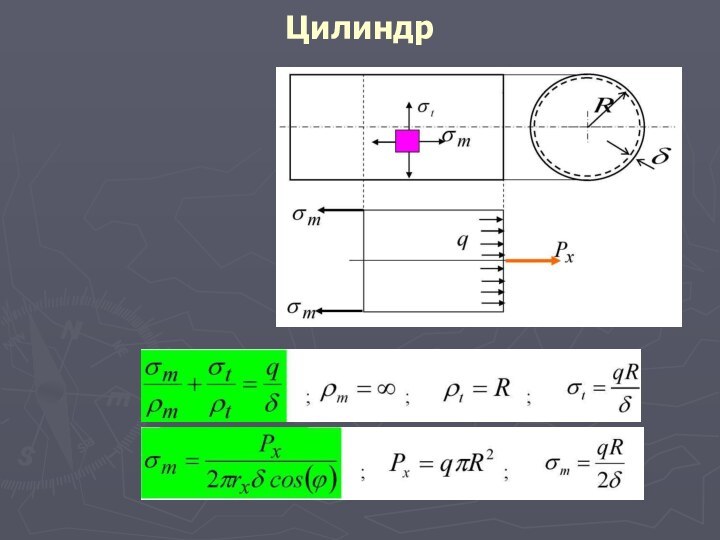
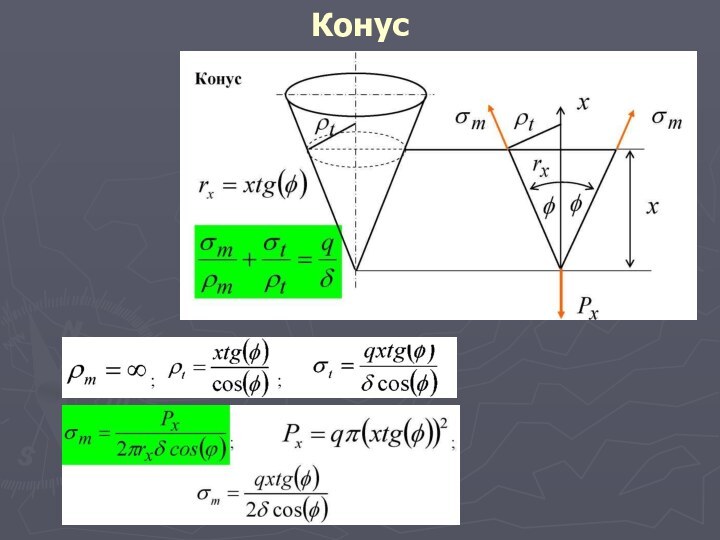
для цилиндра и конуса, у которых меридианами являются прямые линии, rm =∞, а для сферы rm = rt = r. Оболочки с одним вещественным главным радиусом (цилиндр, конус) называются оболочками одинарной кривизны или изогнутыми пластинками. Оболочки с двумя вещественными главными радиусами кривизны в каждой точке (сфера, эллипсоид и тор) называются оболочками двоякой кривизны.
Слайд 8
Оболочками одинарной кривизны могут быть изготовлены с применением
недорогих технологических операций из листового материала с помощью гибки
и сварки. Для изготовления оболочек двоякой кривизны применяются более дорогие операции — штамповка, литье и др.
Используя понятия главных радиусов кривизны гt и гm можно сформулировать условие тонкостенности рассматриваемых далее элементов корпусов технологических аппаратов при D > 0,2 м :
Слайд 9
2.2 Рабочее, расчетное и пробное давления
Рабочее давление р
— максимальное внутреннее избыточное или наружное давление, возникающее при
нормальном протекании рабочего процесса без учета гидростатического давления среды и без учета допустимого кратковременного повышения давления во время действия предохранительного клапана или других предохрани-тельных устройств.
Под расчетным давлением рр для элементов сосудов и аппаратов в рабочих условиях следует понимать давление, на которое производится их расчет.
Расчетное давление принимают, как правило, равным рабочему давлению или выше него:
рр = р + рг, (2.1)
где р, рг соответственно рабочее и гидростатическое давление.
Если (рг/р) ∙ 100% <5%, то рр = р. (2.2)
Слайд 10
Если при полном открытии предохранительного устройства давление в
аппарате составит ртах>1,1р, то расчетное давление находят из соотношения
рр
= 0,9ртах· (2.3)
Для элементов, разделяющих пространства с разными давлениями р1 и р2 (например, в аппаратах с обогревающи-ми рубашками), за расчетное давление следует принимать либо каждое давление в отдельности, либо давление, которое требует большей толщины стенки рассчитываемого элемента. Если в аппарате обеспечивается одновременное действие р1 и р2, то допускается принимать
рр = (р1 - р2) . (2.4)
Под расчетным давлением для элементов сосудов и аппара-тов в условиях испытаний следует понимать давление ри, которому они подвергаются во время пробного испытания.
Пробное давление ри — максимальное избыточное давление, создаваемое при гидравлических (пневматических) испытаниях
Условное давление — это избыточное рабочее
давление среды в аппарате при температуре 20С
Слайд 11
2.3 Марка материала и выбор его допустимых напряжени
Материалы
для изготовления элементов технологическое оборудования, в котором используются тонкостенные
оболочки и пластины, выбираются в соответствии со спецификой их эксплуатации и с учетом изменения в течение заданного срока службы исходных физико-механических свойств под воздействием температуры, давления, рабочей и окружающей среды и протекающих в оборудовании технологических процессов.
Чаще всего используют стальные сосуды и аппараты. В особых случаях находят применение и такие материалы, как алюминий, медь, титан и их сплавы.
ГОСТ F 52630—2006 рекомендует все многообразие применяемых марок сталей подразделить на восемь классов.
Слайд 12
Расчетная температура t стенки — важнейший исходный параметр,
который используется для определения физико-механических свойств материала и допустимых
напряжений, а также при расчете его на прочность с учетом температурных воздействий. Расчетная температура определяется на основании тепловых расчетов, результатов испытаний или опыта эксплуатации аналогичных сосудов.
Допустимые напряжения. Для рабочих условий сосудов и аппаратов, работающих под действием статических однократных нагрузок, допустимые напряжения определяются по формулам метода предельных нагрузок (см. ГОСТ Р 52857.1—2007).
Слайд 13
Прибавки к расчетным толщинам тонкостенных элементов.
Исполнительные толщины рассчитываемых
конструктивных элементов аппаратов, как правило, должны быть больше расчетных
на значение прибавки с:
s>sр + с, (2.5)
где
с = с1 + с2 + с3 (2.6)
Каждая из прибавок с, должна обосновываться в технической документации на проектируемый аппарат. Так, прибавка с1 для компенсации коррозии и эрозии материала аппарата определяется по формуле
с1 =Πτа + сэ (2.7)
где П — проницаемость среды в материал (скорость коррозии); τа — срок службы аппарата; сэ — прибавка для компенсации эрозии. Прибавки с2 (минусовое значение предель-ного отклонения по толщине листа)и с3 (компенсация уменьшения толщины стенки элемента при технологических операциях)учитываются лишь в тех случаях, когда их суммарное значение превышает 5 % от номинальной толщины конструктивного элемента.
Слайд 14
2.4 Напряженное состояние материала упругих осесимметричных оболочек
Для анализа
напряженного состояния материала воспользуемся уже известным нам методом сечений
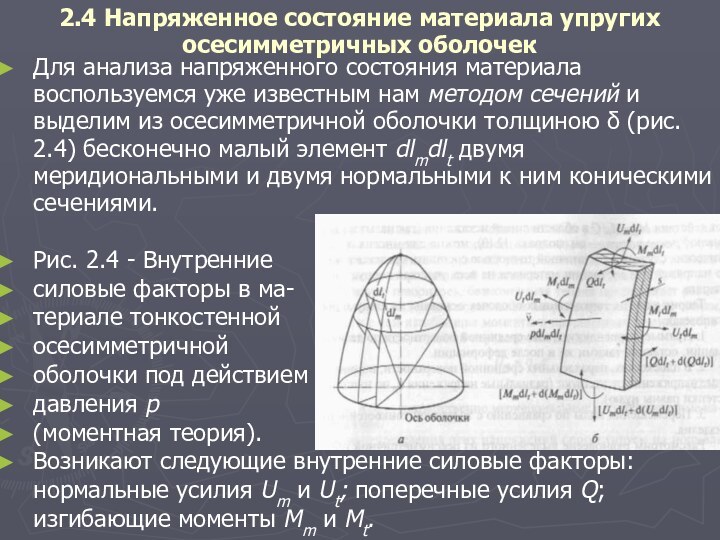
и выделим из осесимметричной оболочки толщиною δ (рис. 2.4) бесконечно малый элемент dlmdlt двумя меридиональными и двумя нормальными к ним коническими сечениями.
Рис. 2.4 - Внутренние
силовые факторы в ма-
териале тонкостенной
осесимметричной
оболочки под действием
давления р
(моментная теория).
Возникают следующие внутренние силовые факторы: нормальные усилия Um и Ut; поперечные усилия Q; изгибающие моменты Мm и Mt.
Слайд 15
Изгибающие моменты Мm и Mt и поперечные усилия
Q имеют существенную величину лишь в ограниченной области вблизи
так называемых линий искажения, поэтому ими можно принебречь.
Значения усилий Umи Ut могут быть легко вычислены по безмоментной теории оболочек, предполагающей равномерное распределение напряжений по толщине стенки и допускающей, что Mm, Mt и Q в сечениях равны нулю.
Теория упругих тонкостенных оболочек основана на принятии следующих гипотез:
Прямые, перпендикулярные к срединной поверхности до деформации, остаются такими же и после деформации.
В плоскостях, параллельных срединной поверхности, нормальные напряжения отсутствуют (радиальные напряжения σρ по толщине стенки равны нулю).
Перемещения малы по сравнению с толщиной тонкостенного изделия.
Слайд 16
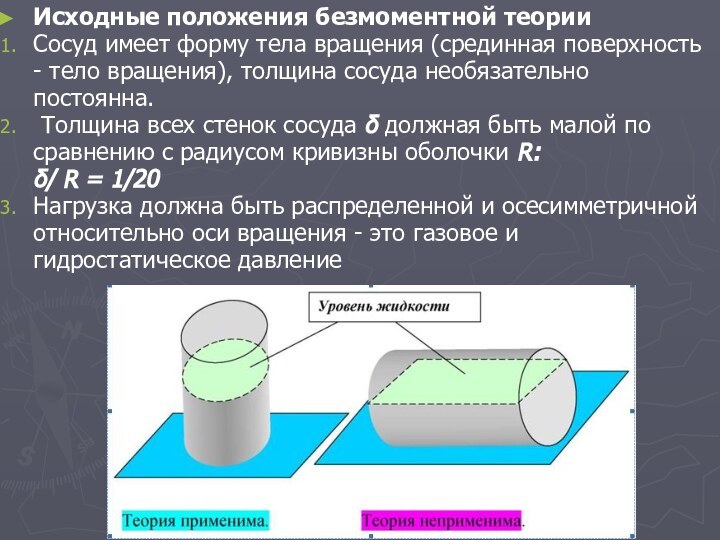
Исходные положения безмоментной теории
Сосуд имеет форму тела вращения
(срединная поверхность - тело вращения), толщина сосуда необязательно постоянна.
Толщина всех стенок сосуда δ должная быть малой по сравнению с радиусом кривизны оболочки R: δ/ R = 1/20
Нагрузка должна быть распределенной и осесимметричной относительно оси вращения - это газовое и гидростатическое давление
Слайд 17
Уравнение Лапласа
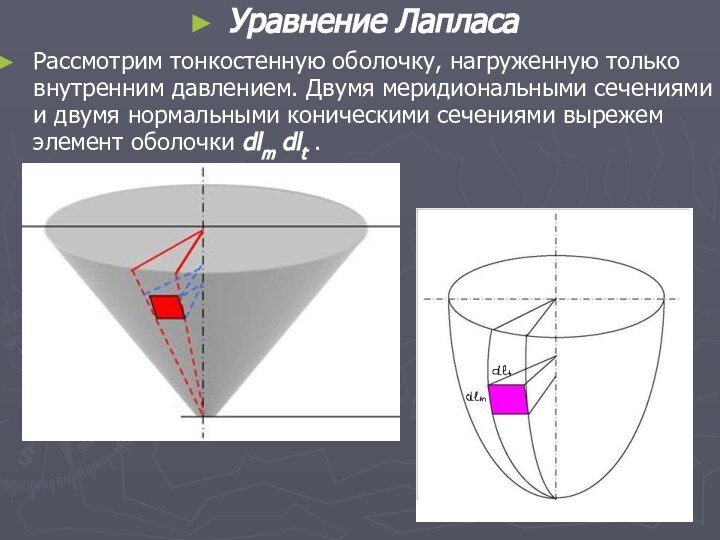
Рассмотрим тонкостенную оболочку, нагруженную только внутренним давлением.
Двумя меридиональными сечениями и двумя нормальными коническими сечениями вырежем
элемент оболочки dlm dlt .
Слайд 18
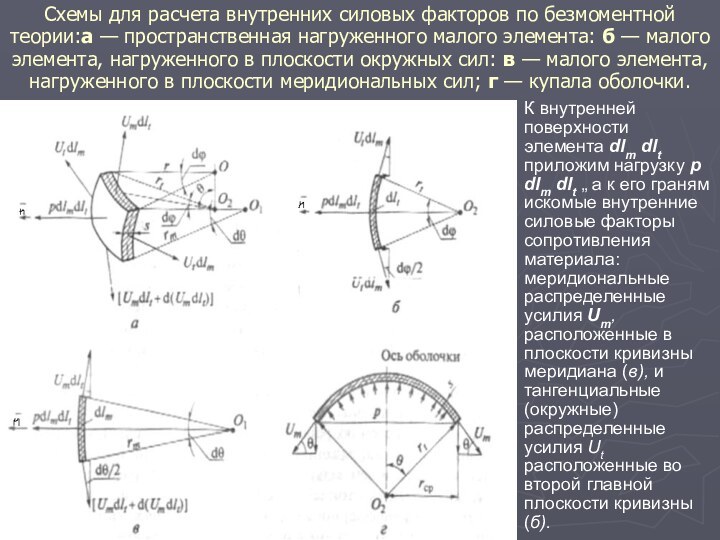
Схемы для расчета внутренних силовых факторов по безмоментной
теории:а — пространственная нагруженного малого элемента: б — малого
элемента, нагруженного в плоскости окружных сил: в — малого элемента, нагруженного в плоскости меридиональных сил; г — купала оболочки.
К внутренней поверхности элемента dlm dlt приложим нагрузку р dlm dlt „ а к его граням искомые внутренние силовые факторы сопротивления материала: меридиональные распределенные усилия Um, расположенные в плоскости кривизны меридиана (в), и тангенциальные (окружные) распределенные усилия Ut расположенные во второй главной плоскости кривизны (б).
Слайд 19
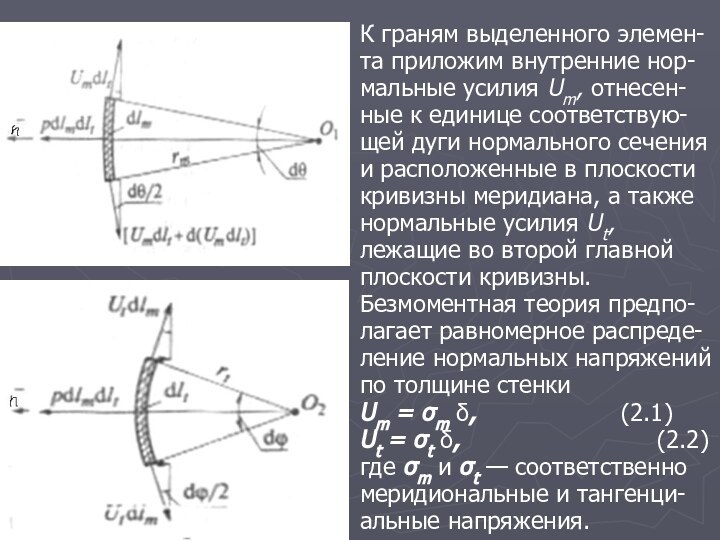
К граням выделенного элемен-та приложим внутренние нор-мальные усилия
Um, отнесен-ные к единице соответствую-щей дуги нормального сечения и
расположенные в плоскости кривизны меридиана, а также нормальные усилия Ut, лежащие во второй главной плоскости кривизны.
Безмоментная теория предпо-лагает равномерное распреде-ление нормальных напряжений по толщине стенки
Um = σm δ, (2.1)
Ut = σt δ, (2.2)
где σm и σt — соответственно меридиональные и тангенци-альные напряжения.
Слайд 20
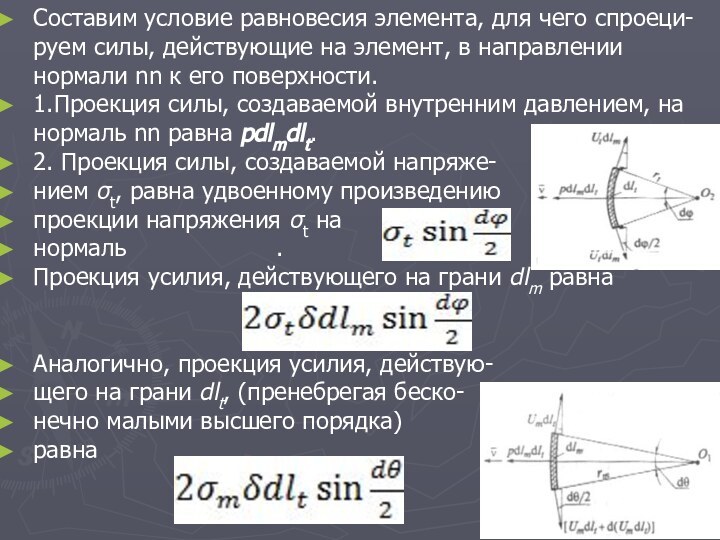
Составим условие равновесия элемента, для чего спроеци-руем силы,
действующие на элемент, в направлении нормали nn к его
поверхности.
1.Проекция силы, создаваемой внутренним давлением, на нормаль nn равна pdlmdlt.
2. Проекция силы, создаваемой напряже-
нием σt, равна удвоенному произведению
проекции напряжения σt на
нормаль .
Проекция усилия, действующего на грани dlm равна
Аналогично, проекция усилия, действую-
щего на грани dlt, (пренебрегая беско-
нечно малыми высшего порядка)
равна
Слайд 21
Спроецировав все силы, приложенные к выделенному элементу, на
направление нормали nn к срединной поверхности силы, действующие на
элемент Σzi·= 0,
Получим выражение (2.3)
Ввиду малости размеров элемента можно принять
Тогда , заменив синусы их аргументами в радианах, и учитывая, что dlm = rmdƟ, dlt = rtdφ получим
prmrtdƟdφ - UtrmdƟdφ – UmrtdƟdφ = 0,
Слайд 22
Сокращаем на dƟdφ :
prmrt - Utrm- Umrt,
= 0,
Делим на rmrt . Откуда
Um/rm+ U
t /rt=p
или с учетом выражений (2.1) и (2.2)
σm δ /rm+ σt δ /rt=p,
Делим на δ и получим окончательно (2.4)
Полученное соотношение (2.3), называемое уравнением Лапласа (1749—1827), связывает безмоментные напряжения σ т и σt в данной точке оболочки с параметрами модели ее геометрической формы и модели нагружения.
Слайд 23
Однако одного этого уравнения недостаточно для определения двух
искомых напряжений σ т и σt , поэтому в
дополнение к уравнению Лапласа рассмотрим равновесие купола этой оболочки, мысленно отсеченного нормальным коническим сечением.
Приравняв проекции искомых
ВСФ и заданной нагрузки р на
ось оболочки, получим
Um·2π rcр sinƟ = р π r 2,
что с учетом Um = σm δ и
соотношения r ≈ rср = rt sinƟ
Запишем :
σm δ ·2π rt sinƟ sinƟ = р π( rt sinƟ)2
После преобразования выражение принимает окончательный вид так называемого допол-
нительного к (2.4) уравнения для расчета
оболочек: (2.5)
Слайд 24
Теорема 1.
Если на какую либо поверхность действует равномерно
распределенное давление q , то независимо от формы поверхности,
проекция равнодействующей Рх сил давления на заданную ось X равна произведению давления q на площадь проекции Fпр данной поверхности на плоскость, перпендикулярную заданной оси.
Слайд 25
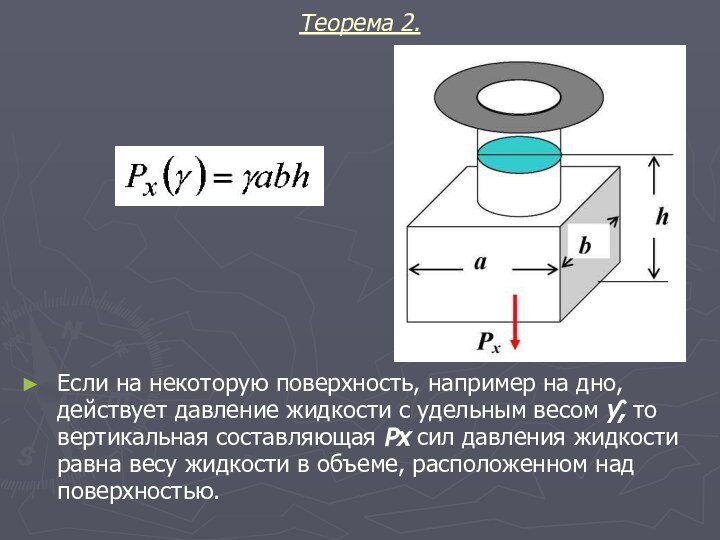
Теорема 2.
Если на некоторую поверхность, например на дно,
действует давление жидкости с удельным весом ƴ, то вертикальная
составляющая Рх сил давления жидкости равна весу жидкости в объеме, расположенном над поверхностью.
Слайд 29
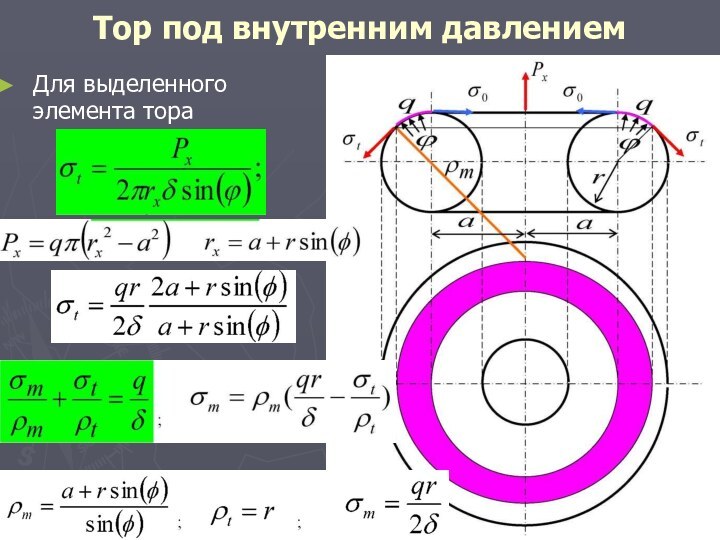
Тор под внутренним давлением
Для выделенного элемента тора
Слайд 30
Окружное (тангенциальное) напряжение в торе, нагруженном внутренним давлением,
минимально на внешней образующей
(ɸ=3 π /2) и максимально
на внутренней образующей(ɸ = π /2). При ( ɸ =0 ) и (ɸ = π) окружное напряжение равно напряжению в прямой трубе с аналогичных размеров.
Выражения (2.4) и (2.5) являются основными уравнениями безмоментной теории оболочек.