Слайд 2
Эпиграф к термодинамике
Это хорошо, Ватсон, что Вы меня
просветили, но я должен это немедленно забыть. Зачем держать
в голове лишние знания?
Артур Конан Дойль,
Рассказы о Шерлоке Холмсе
Слайд 3
Возникновение термодинамики
Термодинамика, как наука зародилась в позапрошлом веке,
как наука о тепловых процессах. Основоположником данной науки является
Сади Карно. Замечательно название его единственной опубликованной работы: «Размышления о движущей силе огня и о машинах, способных развивать эту силу».
Слайд 4
Николя́ Леона́р Сади́ Карно́ (фр. Nicolas Léonard Sadi Carnot);
1 июня 1796 — 24 августа 1832),
В 1824 году вышла первая
и единственная работа Сади Карно — «Размышления о движущей силе огня и о машинах, способных развивать эту силу» (Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance). Эта работа считается основополагающей в термодинамике. В ней был произведён анализ существовавших в то время паровых машин, и были выведены условия, при которых КПД достигает максимального значения (в паровых машинах того времени КПД не превышал 2 %). Помимо этого там же были введены основные понятия термодинамики: идеальная тепловая машина (см. тепловая машина), идеальный цикл (см. цикл Карно), обратимость и необратимость термодинамических процессов
Слайд 5
Развитие термодинамики
Развитие термодинамики шло параллельно со становлением молекулярной
физики. Эти разделы физической науки дополняли и обогащали друг
друга. Накопленный и обобщенный термодинамикой экспериментальный (эмпирический) материал служил фундаментом для построения представлений и теорий молекулярной физики. В свою очередь молекулярная физика увязывала термодинамические понятия с механикой и другими разделами физики, создавая таким образом единую физическую картину мира.
Слайд 6
Исходные понятия термодинамики
С точки зрения учения об атомах
и молекулах термодинамическая система – любое твердое, жидкое или
газообразное тело – состоит из огромного количества частиц. Например, в одном кубическом сантиметре воздуха при нормальных условиях содержится около 2.7⋅1019 молекул. Попытки описания этой системы методами механики явно бессмысленны. Но с другой стороны представление о теле как о системе огромного числа частиц делает более понятным основной постулат или, как говорят, общее начало термодинамики. Оно гласит: каким бы не было состояние изолированного тела оно неизбежно придет к равновесному состоянию при котором прекратятся все макроскопические процессы.
Слайд 7
Параметры системы
Опыт показывает, что состояние термодинамической системы характеризуется
небольшим набором параметров. Для примера, определим эти параметры для
газа, точнее – для идеального газа. С точки зрения молекулярной физики идеальный газ – это газ материальных точек, не имеющих размера, хаотически двигающихся и обменивающихся импульсами друг с другом и со стенками. С точки зрения термодинамики – это система, состояние которой описывается тремя параметрами: давлением, объемом и температурой. Эта модель в силу ее простоты полезна для понимания принципов термодинамики, и мы будем ею широко пользоваться
Слайд 8
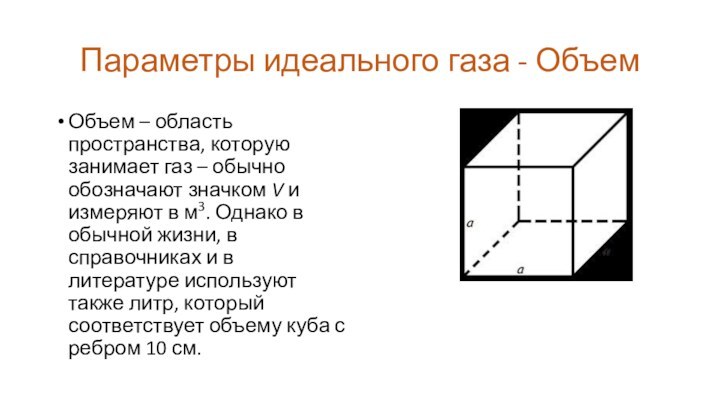
Параметры идеального газа - Объем
Объем – область пространства,
которую занимает газ – обычно обозначают значком V и
измеряют в м3. Однако в обычной жизни, в справочниках и в литературе используют также литр, который соответствует объему куба с ребром 10 см.
Слайд 9
Параметры идеального газа - Давление
С точки зрения молекулярной
физики давление – это импульс, который передают молекулы газа
стенкам в единицу времени. С точки зрения – термодинамики – сила, с которой газ действует на единицу площади. Обычно давление обозначают буквой Р. С его единицами измерения ситуация довольно сложная. Атмосфера, техническая атмосфера, паскаль, бар, торр, мм.рт.ст., все это используемые единицы давления.
Слайд 11
Давление – Единицы измерения
Миллиме́тр рту́тного столба́ (русское обозначение:
мм рт. ст.; международное: mm Hg) — внесистемная единица измерения
давления, равная 101 325 / 760 ≈ 133,322 368 4 Па; иногда называется «торр» (русское обозначение — торр, международное — Torr) в честь Эванджелиста Торричелли.
В Российской Федерации миллиметр ртутного столба допущен к использованию в качестве внесистемной единицы без ограничения срока с областью применения «медицина, метеорология, авиационная навигация»[1]. Международная организация законодательной метрологии (МОЗМ) в своих рекомендациях относит миллиметр ртутного столба к единицам измерения, «которые могут временно применяться до даты, установленной национальными предписаниями, но которые не должны вводиться, если они не используются»[
Слайд 12
Параметры идеального газа - Температура
Молекулярно-кинетическая теория усмотрела глубокую
аналогию между средней кинетической энергией хаотического (или теплового –
эти слова, что характерно, стали в этом контексте почти синонимами) движения молекул и температурой. Если два тела с разной температурой привести в контакт, то рано или поздно их температуры станут равными. Ровно то же самое произойдет со средней энергией двух систем хаотически движущихся частиц, если так или иначе позволить им обмениваться энергией: средние энергии будут выравниваться. Это наблюдение позволило высказать гипотезу о том, что температура пропорциональна средней кинетической энергии молекул
Слайд 13
Температура – Шкала Цельсия
По шкале Цельсия температура замерзания
воды при давлении в 1 атм практически равна 0 C.
Точка кипения воды, выбранная Цельсием в качестве второй реперной точки со значением, по определению равна 100°C. Шкала Цельсия очень удобна с практической точки зрения, поскольку вода очень распространена на нашей планете и на ней основана наша жизнь. Ноль Цельсия — особая точка для метеорологии, поскольку связана с замерзанием атмосферной воды. Шкала предложена Андерсом Цельсием в 1742.
Слайд 17
Термическое уравнение состояния
Слайд 18
Функции состояния
Параметры P,V и T называют функциями состояния.
В термодинамическом смысле это означает, что задание хотя бы
двух из них полностью характеризует состояние системы. В математическом смысле это означает, что любой из них является однозначной функцией двух других. В геометрическом смысле функция двух переменных представляет собой поверхность.
Слайд 19
Равновесные и неравновесные процессы
Классическая термодинамика рассматривает только такие
изменения состояния системы, в которых начальное и конечное состояния
являются равновесными. Это означает, что в газе, например, отсутствуют области сжатия или разрежения, о которых мы говорили в лекции 11, что температура во всех точках газа одинакова и т.д. Промежуточные состояния могут быть любыми, в том числе неравновесными. Изменения в системе могут происходить сами по себе или под действием других систем.
Самопроизвольный переход системы в равновесное состояние называется релаксацией, а время, затраченное на такой переход – временем релаксации. Релаксационные процессы – это процессы выравнивания. Они относятся к неравновесным процессам.
Слайд 20
Равновесные и неравновесные процессы
Слайд 21
Квазистатические процессы для идеального газа
Для того, чтобы сделать
производимые над газом процессы более наглядными часто используют так
называемые P-V, P-T и T-V диаграммы. Мы тоже будем иллюстрировать наши рассуждения с их помощью.
Слайд 22
Изохорический процесс
Так называются нагрев или охлаждение газа при
постоянном объеме. На P-V диаграмме он отображается вертикальной линией.
P-T диаграмма этого процесса
Слайд 23
Изобарический процесс
В этом процессе газ расширяется или сжимается
при постоянном давлении. P-V диаграмме он отображается горизонтальной линией.
T-V диаграмму процесса можно увидеть на рисунке. В соответствии с уравнением состояния в этом случае температура линейно зависит от объема.
Слайд 24
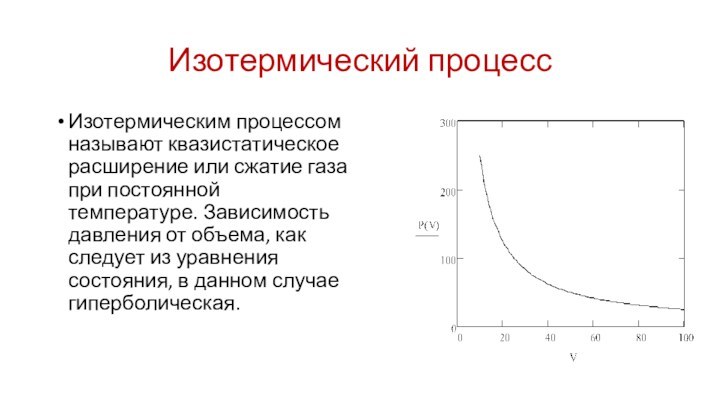
Изотермический процесс
Изотермическим процессом называют квазистатическое расширение или сжатие
газа при постоянной температуре. Зависимость давления от объема, как
следует из уравнения состояния, в данном случае гиперболическая.
Слайд 26
Теплота
Левая часть этого уравнения - δQ – обозначает
тепло (бесконечно малую порцию тепла), переданное системе или отведенное
от нее. С точки зрения молекулярно-кинетической теории δQ – это энергия хаотического движения молекул, переданная термодинамической системе через контакт с более нагретым телом, путем трения, химической реакции и т.д. Сам факт признания, что «тепло» есть не что иное, как энергия был одним из важнейших достижений науки 19 века. Этому способствовал знаменитый опыт Джоуля, установивший механический эквивалент единицы измерения тепла – калории.
Слайд 27
Теплота
Первым термин «калория» применил шведский физик Иоганн Вильке
(1732—1796). Калория определяется, как количество теплоты, необходимое для нагревания
1 грамма воды на 1 кельвин при стандартном атмосферном давлении 101 325 Па. В Российской Федерации калории допущены к использованию в качестве внесистемных единиц без ограничения срока с областью применения «промышленность». В то же время Международная организация законодательной метрологии (МОЗМ) относит калорию к таким единицам измерения, «которые должны быть изъяты из обращения как можно скорее там, где они используются в настоящее время, и которые не должны вводиться, если они не используются»
Слайд 28
Теплота
Для справки: Под калорийностью, или энергетической ценностью, пищи
подразумевается количество энергии, которое получает организм при полном её
усвоении. Чтобы определить полную энергетическую ценность пищи, её сжигают в калориметре и измеряют тепло, выделяющееся в окружающую его водяную баню. Аналогично измеряют и расход энергии человеком: в герметичной камере калориметра измеряют выделяемое человеком тепло и переводят его в «сожжённые» калории — таким образом можно узнать физиологическую энергетическую ценность пищи. Подобным способом можно определить расход энергии на жизнедеятельность и активность для любого человека.
Слайд 29
Теплота
Схема опыта Джоуля представлена на рисунке. В теплоизолированном
сосуде с водой вращаются лопасти мешалки, приводимой в движение
опускающимися грузами, которые подвешены на шнурах, перекинутых через блоки. Вращающиеся лопасти, увлекая воду, вызывают трение одних слоев воды о другие. При трении воды она и сосуд нагреваются; никаких других изменений ни вода, ни остальные части прибора не испытывают. Сила тяжести совершает работу, равную весу груза, умноженному на высоту, с которой он опускается. В начале и в конце опыта все части прибора находятся в покое, так что в результате опыта кинетическая энергия не изменяется. Таким образом, вся совершенная работа вызывает только нагрев воды и прибора, изменение температуры которого Джоулем учитывалось. По данным опыта определялась работа, которую нужно затратить, чтобы повысить температуру 1 г воды на 1º С.
Слайд 30
Теплота
Опыт Джоуля повторялся неоднократно. Брались разные жидкости, разные
сосуды и мешалки, результат был один и тот же:
всегда из одного и того же количества работы получалось одно и то же количество теплоты. Таким образом был установлен механический эквивалент теплоты –
1калория ≈ 4,18 джоулей.
Слайд 32
Внутренняя энергия
Разница в «значках» при теплоте и внутренней
энергии в неслучайна. Она отражает тот факт, что внутренняя
энергия определяется состоянием системы и зависит только от ее параметров, а значит является функцией состояния. Следовательно, dU – дифференциал функции двух переменных (например, объема и температуры). Для идеального газа внутренняя энергия является функцией только температуры. Привносимая же в систему извне теплота, естественно, не может определяться параметрами системы. Это же относится и к работе, которую выполняется над внешней средой и не может не зависеть от ее характеристик. Поэтому для малых величин теплоты и работы употребляется значок δ. Иногда говорят, что тепло и работа являются функциями процесса (а не функциями состояния).
Слайд 35
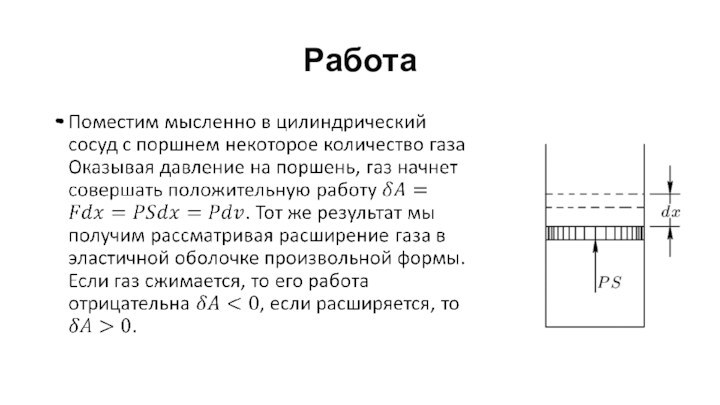
Работа
Очевидно, что работа газа зависит от внешних условий,
или как говорят, от процесса. Для примера на рис.
на P-V диаграмме приведены три варианта процесса, переводящего идеальный газ из состояния 1 в состояние 2. Легко видеть, что работа A совершенная газом в этих процессах разная А142>А12.> А132.
Слайд 37
Теплоемкость изохорического процесса
Слайд 38
Теплоемкость изобарического процесса
Слайд 40
Теплоемкость изотермического процесса
Слайд 46
Работа идеального газа в термодинамических процессах
Слайд 47
Работа идеального газа в термодинамических процессах