теплоотдачей с торца ребра, то есть заменить эти формулами
решениями уравнения (2.34) с граничными условиями
(2.40)
В этом случае распределение температуры по высоте ребра имеет вид
(2.41)
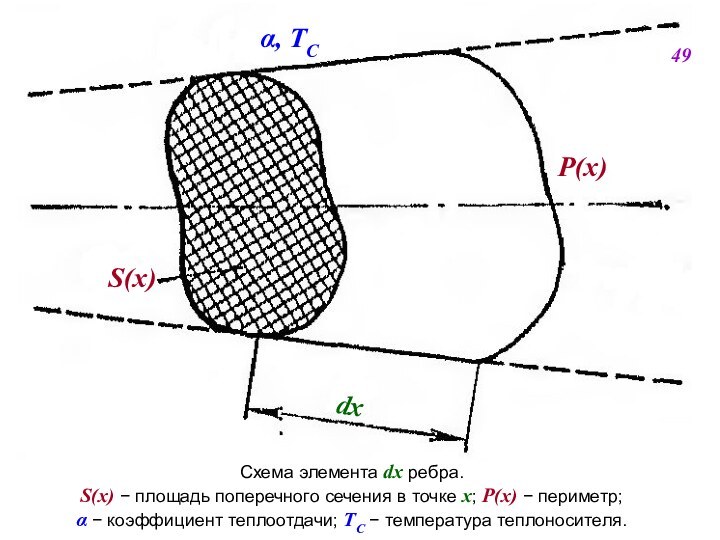
Рассеиваемый участком ребра, имеющим единичную длину, тепловой поток равен
(2.42)
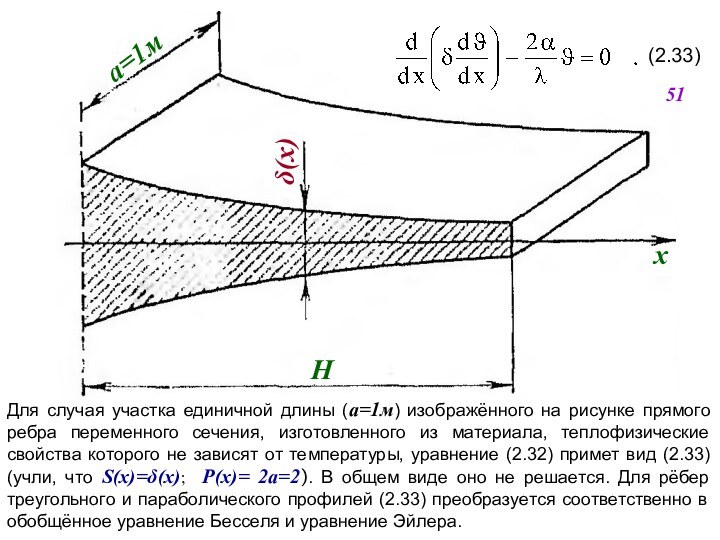
Если ребра имеют большУю относительную высоту H>>δP, то пренебрежение теплоотдачей с торца ребра не приводит к значительным ошибкам.
Однако в реакторостроении рёбра, как правило, имеют небольшую относительную высоту, и, следовательно, теплоотдачей с торца пренебрегать нельзя. Чтобы приближенно учесть теплоотдачу с торца при использовании простых расчётных соотношений (2.41), (2.42), в них вместо действительной высоты ребра подставляется фиктивная высота Н’=Н+δр/2.
Если Bi≤0.25, то рассчитанная таким образом тепловая мощность, рассеиваемая ребром, отличается от результатов расчёта по точному выражению (2.41) не более чем на 7÷8% .
54







![ТЕПЛОМАССОПЕРЕНОС В ЯДЕРНО-ЭНЕРГЕТИЧЕСКИХ УСТАНОВКАХ ОСНОВНЫЕ ТЕРМИНЫ Плотность теплового потока – тепловой поток, отнесённый к площади поверхности, [Вт/м2]](/img/tmb/12/1111599/eb2cea914b5f3fb20227ad93083f58f0-720x.jpg)

![ТЕПЛОМАССОПЕРЕНОС В ЯДЕРНО-ЭНЕРГЕТИЧЕСКИХ УСТАНОВКАХ Коэффициент теплоотдачи – присутствую-щий формуле (*) множитель (коэффициент) про-порциональности α, [Вт/(м2·К)]. Коэффициент](/img/tmb/12/1111599/7f745f2aa8161a9d9a89f48bd9152a9a-720x.jpg)


![ТЕПЛОМАССОПЕРЕНОС В ЯДЕРНО-ЭНЕРГЕТИЧЕСКИХ УСТАНОВКАХ Коэффициент теплопередачи – стоящий в формуле (**) множитель (коэффициент) пропорциональности k, [Вт/(м2·К)]. Коэффициент](/img/tmb/12/1111599/c42f252625caa9d54aa50ae835977603-720x.jpg)






























































![ТЕПЛОМАССОПЕРЕНОС В ЯДЕРНО-ЭНЕРГЕТИЧЕСКИХ УСТАНОВКАХ 1-я стадия2-я стадияτ1τ2τln[TenvT(,)]ln(TenvT2)ln(TenvT1) 180Oψψψ180Oψξ=0ξ=RРисунок Логарифм разницы температур 91](/img/tmb/12/1111599/50975d65e9bb2f3d6577335d4de655b4-720x.jpg)







































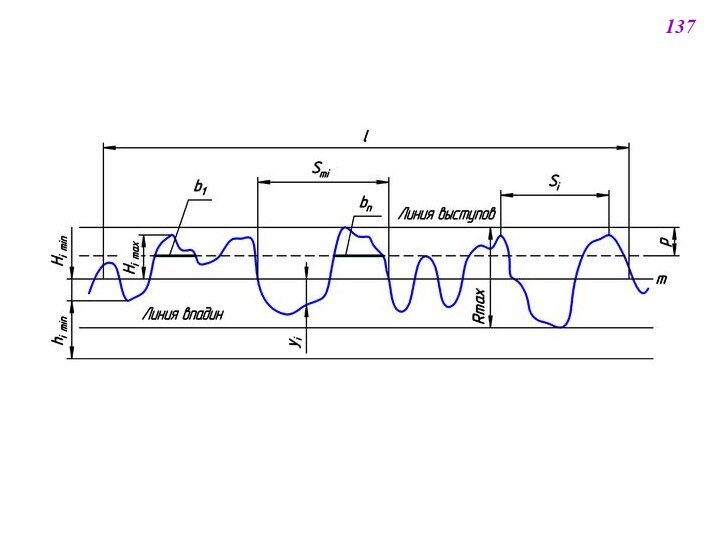



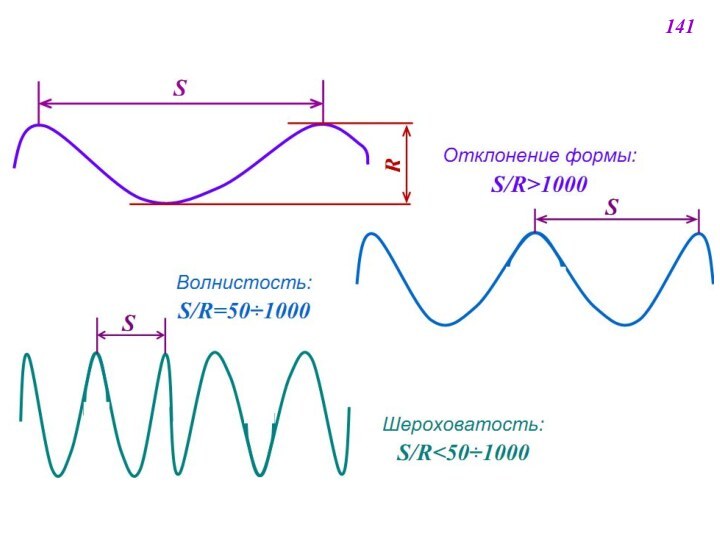
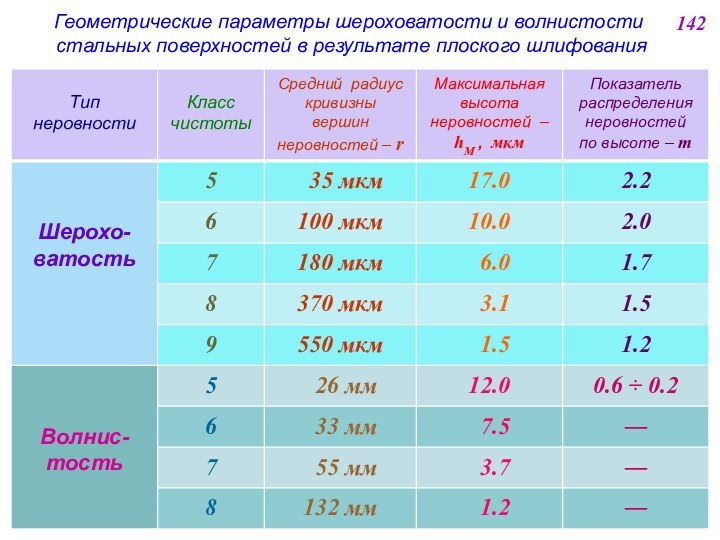

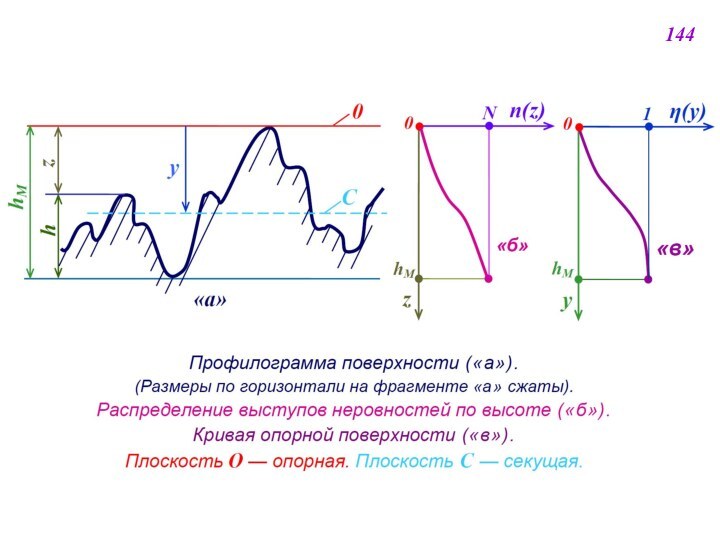
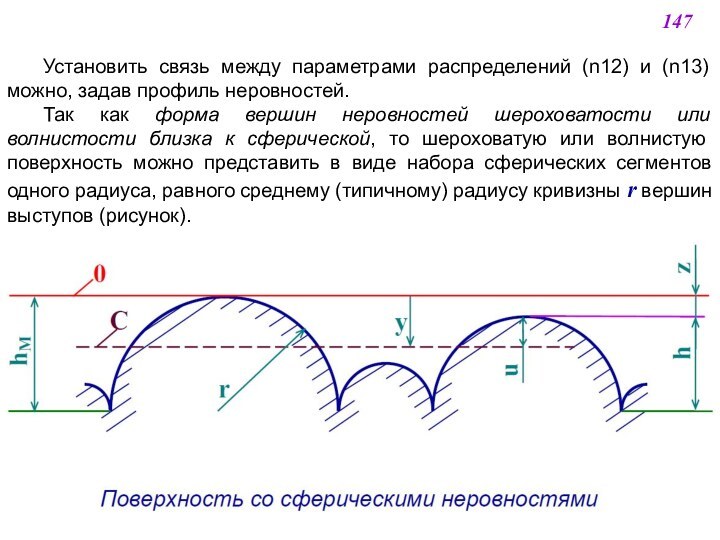
![ТЕПЛОМАССОПЕРЕНОС В ЯДЕРНО-ЭНЕРГЕТИЧЕСКИХ УСТАНОВКАХ N [м–2] – полное число выступов неровностей на единичной площадке (участке поверхности,](/img/tmb/12/1111599/816ec71d20f00323242f8d4a2886c805-720x.jpg)