Слайд 2
Закон Кулона
Система неподвижных электрических зарядов взаимодействует между собой
посредствам электрического поля. Взаимодействие осуществляется не мгновенно, а со
скоростью распространения света с = 3⋅108 м/с.
Основной закон электростатического взаимодействия неподвижных то
чечных (размеры заряженных тел на много меньше расстояния между ними) был сформулирован в 1785 г. французским физиком Шарлем Огюстом Кулоном (1736 – 1806).
Закон Кулона: сила электрического взаимодействия между двумя неподвижными точечными зарядами в вакууме пропорциональна произведению модулей их зарядов и обратно пропорциональна квадрату расстояния между ними:
где
Слайд 3
При решении задач закон Кулона удобнее представлять в
скалярной форме
Кулон (Кл) – единица электрического заряда определяемая как
количество электричества, проходящее через поперечное сечение проводника при силе тока в 1 А за время 1с.
Кулон является весьма большой величиной. Так, например, два заряда q1 =q2 = 1Кл, помещённые на расстояние r = 1 м, взаимодействуют в соответствии с (1.3) с силой F ≅ 9⋅109Н ( вес 900 тыс. тонн груза).
На практике используют чаще всего микрокулоны ( 1мкКл = 10 – 6 Кл ) и нанокулоны (1нКл = 10 – 9 Кл).
Влияние среды на взаимодействие электрических зарядов определяется безразмерной величиной ε − диэлектрической проницаемостью среды. Диэлектрическая проницаемость показывает, во сколько раз сила кулоновского взаимодействия в данной среде меньше чем в вакууме:
Слайд 4
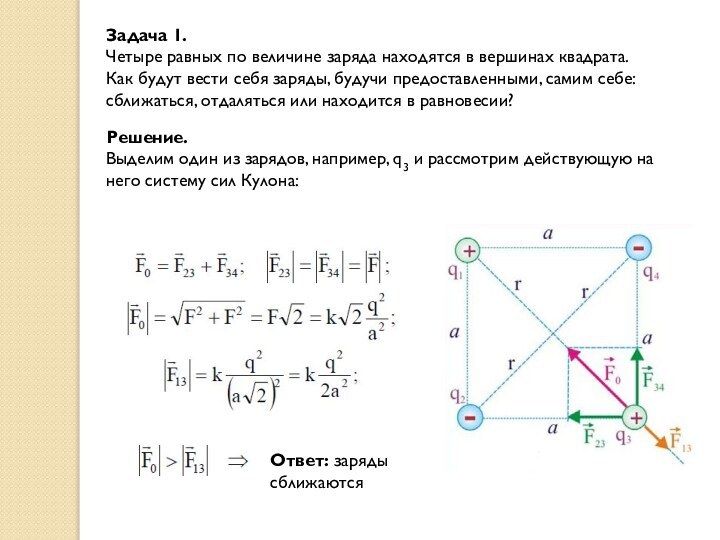
Задача 1.
Четыре равных по величине заряда находятся в
вершинах квадрата.
Как будут вести себя заряды, будучи предоставленными, самим
себе: сближаться, отдаляться или находится в равновесии?
Решение.
Выделим один из зарядов, например, q3 и рассмотрим действующую на него систему сил Кулона:
Ответ: заряды сближаются
Слайд 5
Задача 2.
К шёлковым нитям длиной l = 0,2
м, точки подвеса которых находятся
на одном уровне на расстоянии
х = 0,1 м друг от друга, подвешены два маленьких шарика массой m = 50 мг каждый. При сообщении шарикам равных по модулю и противоположных по знаку зарядов, шарики сблизились на расстояние r = 2 см. Определить заряды, сообщённые шарикам.
Решение.
Угол отклонения нити от равновесно-
го положения ϕ определим из прямоугольного треугольника ΔOAB:
Натяжение нити:
Отсюда
Ответ: qx = 2,1 нКл
Слайд 6
Задача 3.
Два одинаковых металлических шарика заряжены так, что
заряд одного из них в пять раз больше другого.
Шарики привели в соприкосновение и раздвинули на прежнее расстояние. Как изменится сила взаимодействия, если шарики были заряжены:
1.одноимённо? 2. разноимённо?
Решение.
Одноименно заряженные шарики:
2. Разноименно заряженные шарики:
Слайд 7
Электрическое поле
Электрическим полем называется часть пространства, в котором
прояв
ляются электрические силы. Представление об электрическом поле было введено
в науку М. Фарадеем в 19 в. Согласно Фарадею, каждый покоящийся заряд создаёт в окружающем пространстве электрическое поле. Поле одного заряда действует на другой заряд, и наоборот; так осуществляется взаимодействие зарядов.
Для характеристики электрических полей оказалось более полезным рас
сматривать не силу Кулона в каждой точке поля, а отношение силы Кулона к пробному заряду.
Для изолированного точечного заряда, расположенного в вакууме или
сухом воздухе, напряжённость создаваемого им электрического поля определяется непосредственно из уравнения закона Кулона:
Майкл Фараде́й (1791 -1867) — английский физик-экспериментатор, химик . Основоположник учения об электромагнитном поле.
Слайд 8
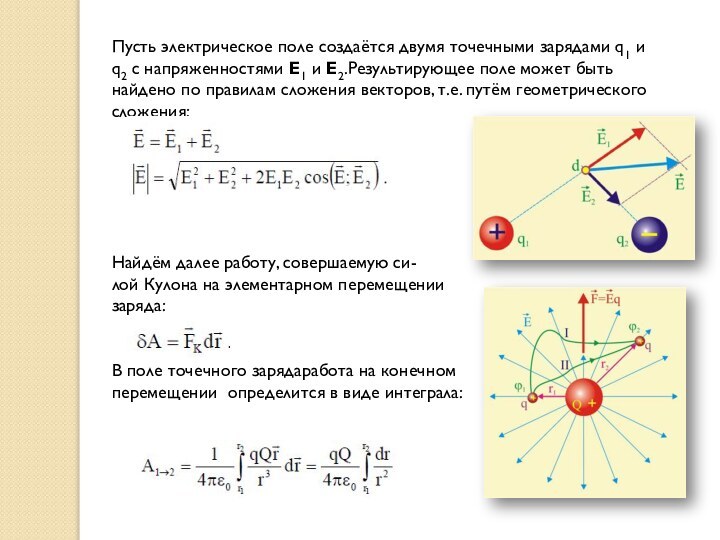
Пусть электрическое поле создаётся двумя точечными зарядами q1
и q2 с напряженностями E1 и E2.Результирующее поле может
быть найдено по правилам сложения векторов, т.е. путём геометрического сложения:
Найдём далее работу, совершаемую си-
лой Кулона на элементарном перемещении
заряда:
В поле точечного зарядаработа на конечном
перемещении определится в виде интеграла:
Слайд 9
Интеграл работы не зависит от положения начальной и
конечной точек, а так же от формы траектории, по
которой перемещается заряд q, а определяется только положениями начальной и конечной точек перемещения:
Свойство потенциальности обусловлено тем обстоятельством, что в
электростатических полях проявляются консервативные силы, дающие возможность каждую точку поля охарактеризовать с энергетических позиций. Работа, совершаемая в электростатическом поле, совершается за счёт уменьшения потенциальной энергии (П) заряда.
Полученные выше уравнения работы показывают, что так же как и напря-
жённость, работа пропорциональна величине заряда. В этой связи целесообразно рассмотреть отношение потенциальной энергии поля П к пробному заряду q , что даст новую характеристику поля − потенциал.
Работу электрического поля при перемещении заряда q из точки 1 в
точку 2 можно определить как разность потенциалов поля в этих точках:
где φ1=П1/q, φ2=П2/q.
Слайд 10
Задача 4.
Проводящий шар радиусом R = 0,3 м
имеет поверхностную плотность
заряда σ = 2⋅10 − 8 Кл/м2.
Найти напряжённость поля в точке, находящейся на расстоянии r = 0,7 м от поверхности шара, находящемся в жидкости с диэлектрической проницаемостью ε = 2.
Решение.
Задача 5.
В какой среде точечный заряд q = 4,5⋅10 − 7 Кл создаёт на расстоянии r =
5 см от себя электрическое поле напряжённостью Е = 2⋅104 В/м?
Решение.
Слайд 11
Задача 6.
Два заряда q1 = 2⋅10− 8 Кл
и q2 = 1,6⋅10 − 6 Кл расположены на
расстоянии
L = 5 см друг от друга. Найти напряжённость поля в точке, удалённой от первого заряда на r1 = 3 см и от второго заряда на r2 = 4 см.
Решение.
Модули напряжённостей поля,
создаваемого зарядами в заданной
точке:
Заданные расстояния указывают, что ΔADB прямоугольный, т.е. α = π/2, следовательно:
Слайд 12
Электрическая ёмкость
Если нейтральный проводник поместить в электрическое поле,

то через короткое время за счёт индукции произойдёт разделение
зарядов проводника, которые разместятся на его поверхности напряжённость поля внутри проводника будет равна нулю, а поверхность будет представлять собой эквипотенциальную поверхность.
Электрический потенциал на поверхности проводника пропорционален его заряду:
Q = Cφ
Коэффициент пропорциональности между зарядом и потенциалом проводника C называется электроёмкостью.
Электрическая ёмкость проводника или системы проводников – физическая величина, характеризующая способность накапливать заряды. Понятие ёмкости сложилось исторически в те времена, когда электрический заряд представлялся неосязаемой жидкостью, содержащейся в проводнике в большем или меньшем количестве.
Электрическая ёмкость измеряется в фарадах [Ф], 1фарада – ёмкость такого проводника, при которой увеличение заряда проводника на 1 кулон увеличивает потенциал на 1 вольт. Такой ёмкостью обладает сфера радиусом 9⋅109 м (радиус Земли равен ≅ 6,4⋅106 м).
Слайд 13
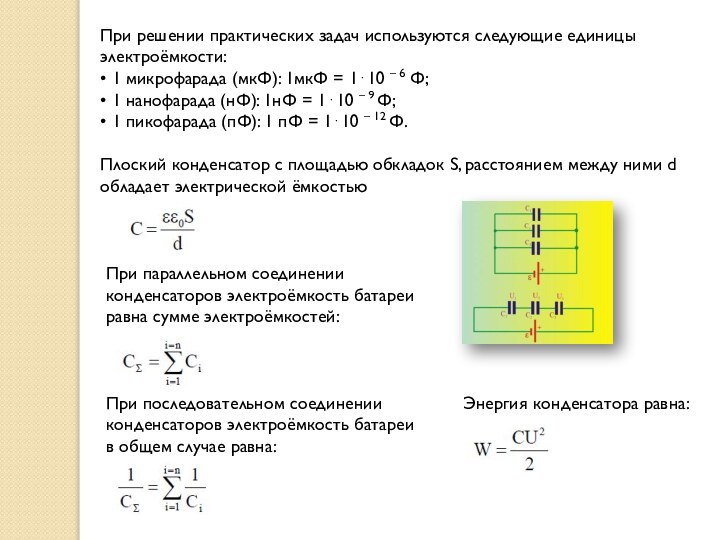
При решении практических задач используются следующие единицы электроёмкости:
•
1 микрофарада (мкФ): 1мкФ = 1⋅10 – 6 Ф;
•
1 нанофарада (нФ): 1нФ = 1⋅10 – 9 Ф;
• 1 пикофарада (пФ): 1 пФ = 1⋅10 – 12 Ф.
Плоский конденсатор с площадью обкладок S, расстоянием между ними d обладает электрической ёмкостью
При параллельном соединении
конденсаторов электроёмкость батареи равна сумме электроёмкостей:
При последовательном соединении конденсаторов электроёмкость батареи
в общем случае равна:
Энергия конденсатора равна:
Слайд 14
Задача 7.
Определить потенциал точки, расположенной на расстоянии r
= 2 м от
точечного заряда q = 3⋅10 −
7 Кл.
Решение.
Задача 8.
Шар радиусом R = 19 см заряжен до потенциала φ = 500 В. Определить
заряд шара и потенциал точки, находящейся на расстоянии r = 41 см от
поверхности шара.
Решение.
Слайд 15
Задача 9.
Какое расстояние должно быть между двумя плоскими
пластинами,
чтобы при разности потенциалов U = 500 В напряжённость
поля составила Е =2⋅103 В/м? Какая сила будет действовать на пылинку с зарядом q = 2⋅10 − 8 Кл в этом поле? С каким ускорением станет двигаться пылинка массой m = 10 − 9 кг?
Решение.
Расстояние между пластинами:
Сила Кулона, действующая на пылинку:
Ускорение пылинки:
Слайд 16
Задача 10.
До какого потенциала зарядился сферический проводник радиусом
R
= 0,1 м, если ему сообщили заряд Q =
2⋅10 − 10 Кл?
Решение.
Задача 11.
Ёмкость двух металлических шаров С1 = 10 пФ и С2 = 20 пФ, они несут
заряды Q1 = 17 нКл и Q2 = 30 нКл. Будут ли перемещаться электроны при соединении шаров проводником?
Решение.
Потенциалы шаров:
Так как потенциалы разные, будет перемещене заряда.
Слайд 17
Задача 12.
К пластинам плоского конденсатора, находящимся на расстоянии
друг
от друга d = 4 мм, приложена разность потенциалов
U = 160 В. Пространство между пластинами заполнено стеклом (ε = 7), площадь обкладок s = 10 − 2м2. Определить величину заряда на пластинах.
Решение.
Ёмкость конденсатора:
Заряд на пластинах:
Задача 13.
Плоский конденсатор, между обкладками которого находится слюдя-
ная пластинка (ε = 6), присоединен к аккумулятору. Заряд конденсатора Q1 =14 мкКл. Какой заряд пройдёт через аккумулятор при внезапном удалении пластинки?
Решение.
Слайд 18
Постоянный электрический ток
Выделим в проводнике физически
малый объём, внутри
которого
направленно движутся со средней ско
ростью носители заряда. Эта скорость
называтся дрейфовой.
Пусть в рассматриваемом металлическом проводнике в единице его объёма содержится n электронов. Выделим далее элементарную площадку dS, перпендикулярную вектору дрейфовой скорости, являющуюся основанием цилиндра с протяжённостью udt. Все носители заряда, содержащиеся внутри этого цилиндра, через площадку dS за время dt перенесут заряд
dq = neu dS dt
Введем понятие плотности тока:
Слайд 19
Георг Симон Ом в 1825 г. опубликовал работу,
в которой установил экспериментально зависимость между силой тока I
и напряжением на концах проводника U (закон Ома для участка цепи)
где R − электрическое сопротивление, измеряемое в Омах, G − проводимость материала проводника, ρ − удельное сопротивление, измеряемое в Ом⋅м, S −площадь поперечного сечения проводника, l − его длина.
Сопротивление зависит от внешних условий, особенно от температуры
проводника. Экспериментально установлено, что
Слайд 20
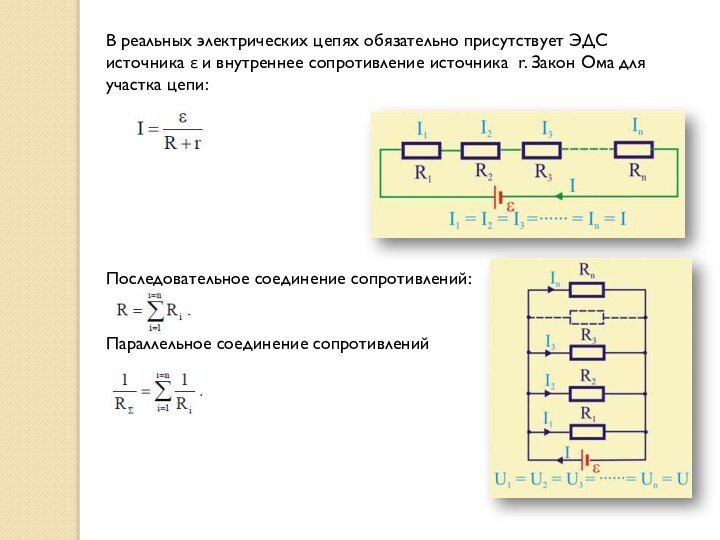
В реальных электрических цепях обязательно присутствует ЭДС источника
ε и внутреннее сопротивление источника r. Закон Ома для
участка цепи:
Последовательное соединение сопротивлений:
Параллельное соединение сопротивлений
Слайд 21
Правила Кирхгофа
Первое правило Кирхгофа. Это правило относится к
узлам электрических цепей, т.е. точкам цепи, в которых сходится
не менее трёх проводников. Если, принять за положительные направления подходящих к узлу токов, а отходящих − за отрицательные, то алгебраическая сумма токов в любом узле должна быть равна нулю:
Второе правило Кирхгофа является обобщением закона Ома и относится к
замкнутым контурам разветвлённой цепи.
В любом замкнутом контуре электрической цепи алгебраическая сумма произведений токов на сопротивления соответствующих участков контура равна алгебраической сумме ЭДС в этом контуре:
Слайд 22
Использование правил Кирхгофа может привести к достаточно сложным
алгебраическим уравнениям. Ситуация упрощается если цепь содержит некие симметричные
элементы, в этом случае могут существовать узлы с одинаковыми потенциалами и ветви цепи с равными токами, это существенно упрощает уравнения.
Классическим примером такой ситуации является задача об определении сил токов в кубической фигуре, составленной из одинаковых сопротивлений:
В силу симметрии цепи по-
тенциалы точек 2,3,6 , так жекак и точек 4,5,7 будут одинаковы, их можно соединять, так
как это не изменит в плане распределения токов, но схема существенно упростится.
Слайд 23
Закон Джоуля − Ленца
В неподвижном проводнике движущиеся носители
за-
ряда, в соответствие с классической теорией электропроводности, сталкиваются с
атомами металла и, отдавая им энергию, повышают тем самым температуру проводника. Это было замечено и экспериментально, что всякий проводник, по
которому течёт ток, имеет температуру выше окружающей среды.
Другими словами, носители заряда, получая энергию от электрического поля, часть её расходуют на нагревание проводника.
Если сила тока и разность потенциалов в проводнике во времени не меняются, то количество тепла, выделившееся в проводнике за время Δt
Этот закон установлен был в 1841г. Дж. Джоулем и в 1842 г. независимо, Эмилем Христофоровичем Ленцем, профессором Петербургского университета.
Слайд 24
Задача 14.
Найти скорость упорядоченного движения электронов в проводнике
сечением S = 5 мм2 при силе тока I
= 10 А, если концентрация электронов проводимости n = 5⋅1028 м − 3.
Решение.
Задача 15.
Сколько электронов проходит через поперечное сечение проводника за время τ = 5 мс при силе тока I = 48 мкА?
Решение.
Слайд 25
Задача 16.
Как изменится сопротивление не изолированного проводника, если
его
сложить пополам, а затем плотно скрутить?
Решение.
Поскольку
то складывание проводника
пополам уменьшает его длину вдвое, а поперечное сечение увеличивает в два раза, в итоге сопротивление проводника уменьшится в 4 раза.
Задача 17.
Лампочка с вольфрамовой нитью при t0 = 0 0С обладает сопротивлени-
ем R0 = 1 Ом, а при температуре t1 = 2000 0C сопротивление R1 = 9,4 Ом. Определить температурный коэффициент сопротивления вольфрама.
Решение.
Слайд 26
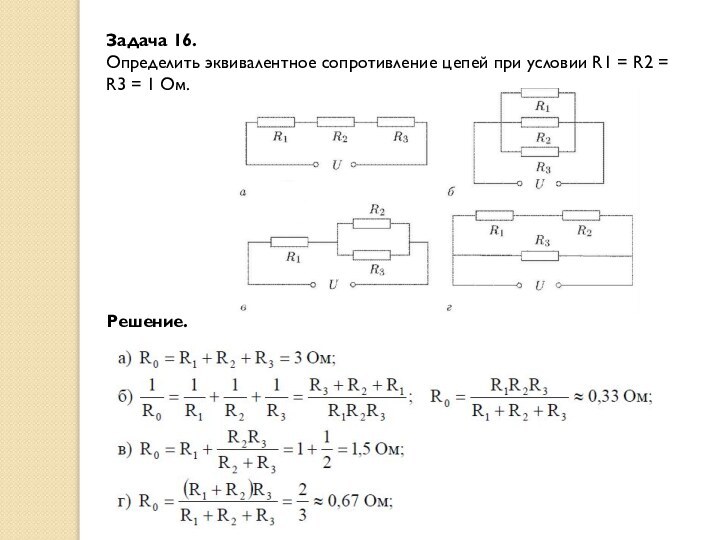
Задача 16.
Определить эквивалентное сопротивление цепей при условии R1
= R2 =
R3 = 1 Ом.
Решение.
Слайд 27
Задача 17.
Электродвижущая сила источника ε = 6 В.
При внешнем сопротивле-
нии цепи R = 1 Ом сила
тока равна I = 3 А. Определить силу тока короткого замыкания.
Решение.
Внутреннее сопротивление источника:
Сила тока короткого замыкания:
Задача 18.
Внутреннее сопротивление элемента в 5 раз меньше сопротивления
внешней нагрузки элемента с ЭДС ε = 10 В. Определить, во сколько раз напряжение на зажимах элемента отличается от его ЭДС.
Решение.
Слайд 28
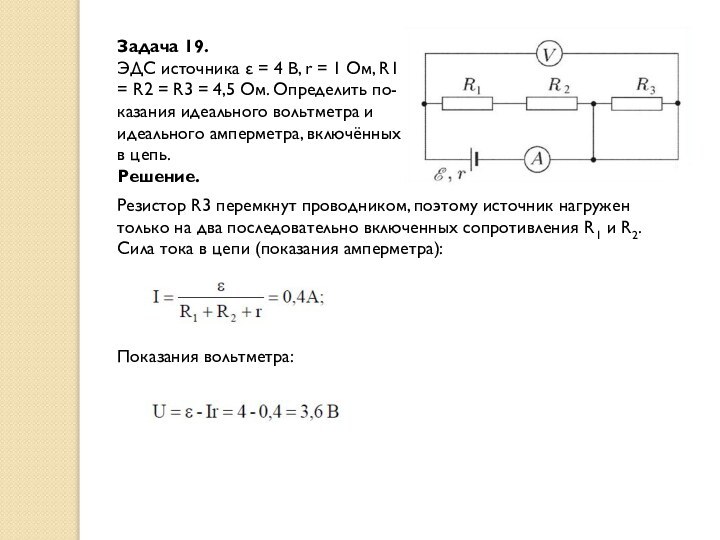
Задача 19.
ЭДС источника ε = 4 В, r
= 1 Ом, R1 = R2 = R3 =
4,5 Ом. Определить по-
казания идеального вольтметра и идеального амперметра, включённых в цепь.
Решение.
Резистор R3 перемкнут проводником, поэтому источник нагружен только на два последовательно включенных сопротивления R1 и R2.
Сила тока в цепи (показания амперметра):
Показания вольтметра:
Слайд 29
Задача 20.
В электрическом чайнике вода закипает через τ1
= 12 минут после его
включения в сеть. Нагревательный элемент
чайника намотан проводом длиной l1 = 4,5 м. Как следует изменить нагревательный элемент, чтобы вода в чайнике закипала через время τ2 = 8 минут?
Решение.
При U = cost, мощность нагревателя определяется силой тока, поэтому
для увеличения мощности требуется уменьшить сопротивление нагревателя:
Слайд 30
Задача 21.
На металлическую пластину падает электромагнитное излучение, вы-
бивающее
электроны из пластинки. Максимальная кинетическая энергия электронов, вылетевших из
пластинки в результате фотоэффекта, составляет K =6 эВ, а энергия падающих фотонов в 3 раза больше работы выхода из металла. Определить величину работы выхода.
Решение.
Задача 22.
Если полная энергия электрона в атоме увеличилась на Δε = 3⋅10 − 19
Дж, то фотон с какой длиной волны электрон поглотил?
Решение.
Величина изменения энергии электрона должна быть равна энергии фотона
Слайд 31
Задача 23.
Чему равен угол падения светового луча в
воздухе на поверхность
воды, если угол между преломлённым и отражённым
лучами равен 90о?
Решение.
Имеем
По закону преломления
Отсюда
Поэтому