Презентация на тему Проблемные темы школьной физики

в неинерциальных системах
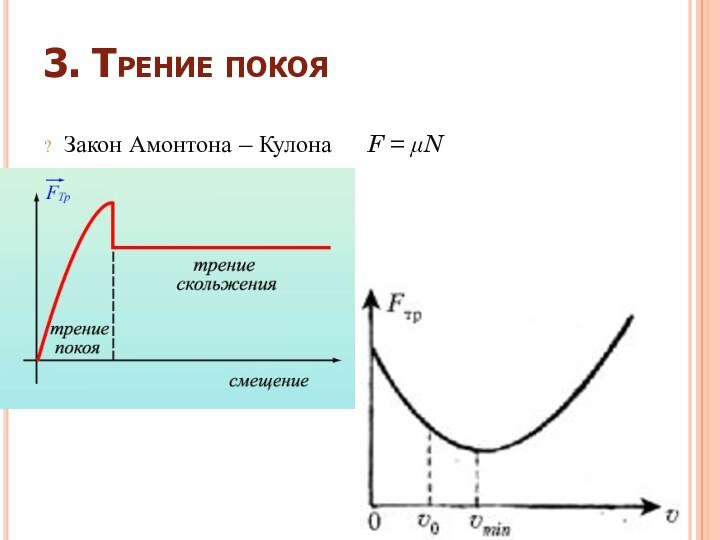
3. Трение покоя
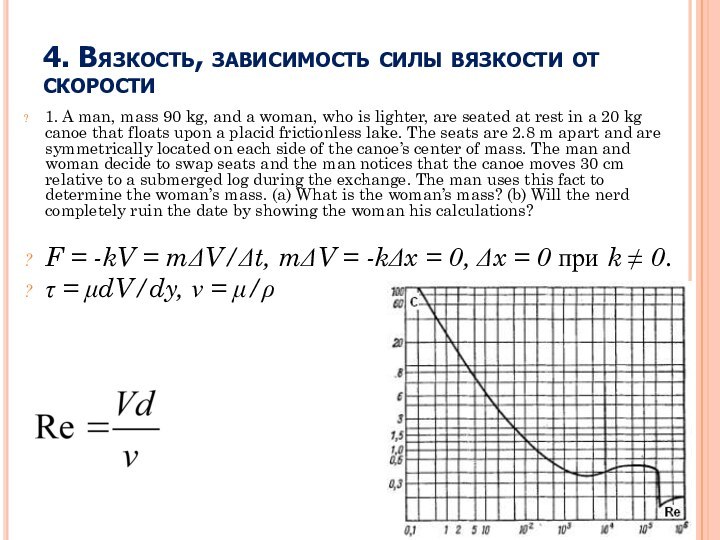
4. Вязкость, зависимость вязкости от

скорости
5. Уравнение Бернулли, уравнение неразрывности
6. Электростатика и квазистатика
7. Сила Кулона и сила Лоренца
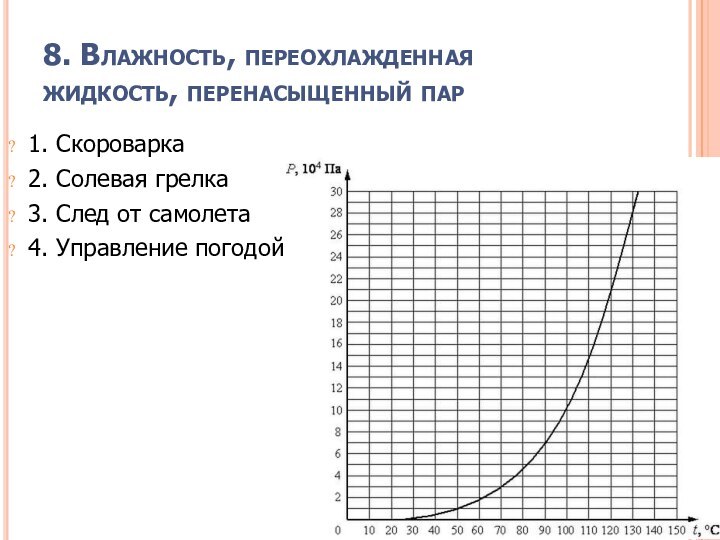
8. Влажность, переохлажденная жидкость, перенасыщенный пар
9. Теплоемкость газов
10. Температура
11. Обратимые и необратимые процессы, энтропия
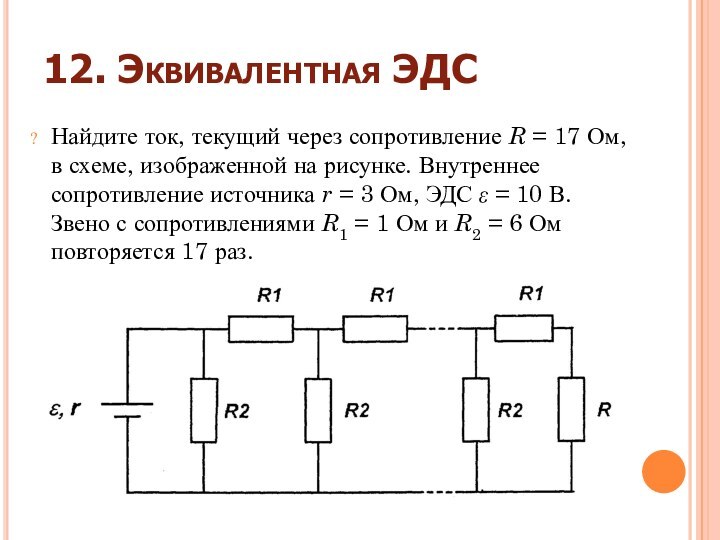
12. Эквивалентная ЭДС
13. Квантование момента импульса
14. Принцип неопределенности
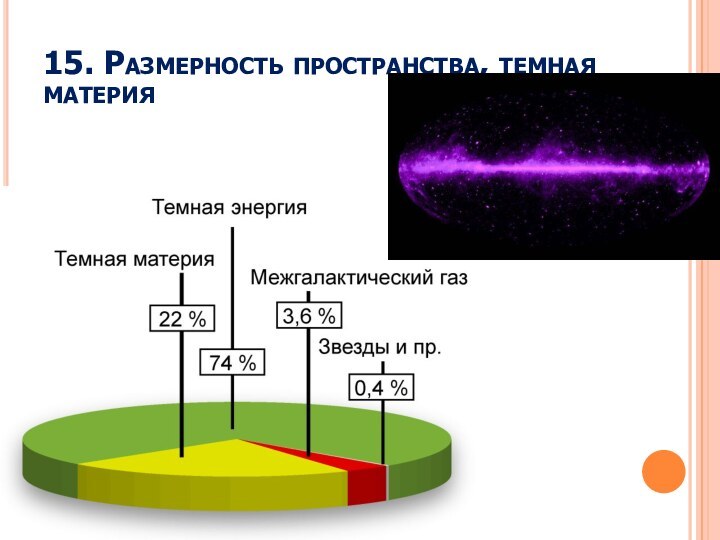
15. Размерность пространства
16. Темная материя

εΕ σ = F/S – напряжение (stress)
ε = Δx/l –

относительная деформация
Е – модуль Юнга
k = SE/l
Даны две пружины из одинакового материала. Диаметры витков пружин 3 мм и 9 мм, их длины 1 см и 7 см, диаметры проволок 0,1 мм и 0,3 мм. Чему равна жесткость второй пружины, если жесткость первой 14 Н/м?

man, mass 90 kg, and a woman, who is

lighter, are seated at rest in a 20 kg canoe that floats upon a placid frictionless lake. The seats are 2.8 m apart and are symmetrically located on each side of the canoe’s center of mass. The man and woman decide to swap seats and the man notices that the canoe moves 30 cm relative to a submerged log during the exchange. The man uses this fact to determine the woman’s mass. (a) What is the woman’s mass? (b) Will the nerd completely ruin the date by showing the woman his calculations?

F = -kV = mΔV/Δt, mΔV = -kΔx = 0, Δx = 0 при k ≠ 0.
τ = μdV/dy, ν = μ/ρ

механик и математик, один из создателей кинетической теории газов,

гидродинамики и математической физики.

Уравнение неразрывности: ρVS = const
Учет силы Лоренца (МГД): j×B⋅x

= c/ν. Для ν = 50 Гц λ/4 =

1500 км.

j >> jсм (токи смещения, jсм = ε0 dE/dt) или
τхар >> ε0/λпр (λпр - проводимость, j = λпрE)

а
однонаправленные токи притягиваются. Почему?

грелка
3. След от самолета
4. Управление погодой

Изобарический процесс: Cp = 5/2⋅νRT
3. Изотермический процесс: CT =

0
4. Адиабатический процесс: CA = ∞
5. P = -aV+b: С < 0 (на участке).

≈ 1/(nσv) или vпоршня

Инверсионная (лазерная) среда – Т(К) < 0 (формально)
4. Гиперзвуковой поток (М>>1) – Тколеб>Т (в аэродинамической трубе), Тколеб< Т (в полете)

= k⋅lnW
W – число микросостояний

= 17 Ом, в схеме, изображенной на рисунке. Внутреннее

сопротивление источника r = 3 Ом, ЭДС ε = 10 В. Звено с сопротивлениями R1 = 1 Ом и R2 = 6 Ом повторяется 17 раз.

1913)
Еn = - me4/2h2n2 = -13,6 эВ/n2

Я обнаружил серьезное

затруднение: как может электрон знать, с какой частотой он должен колебаться, переходя из одного стационарного состояние в другое? Мне кажется, что электрон знает заблаговременно, где он собирается остановиться (Резерфорд).

«Если мы собираемся сохранить эти проклятые квантовые скачки, то я жалею, что вообще имел дело с квантовой теорией! (Шредингер)

10 г, l = 10 см)