Слайд 2
Виды и категории сил в природе
Одно из
простейших определений силы: влияние одного тела (или поля) на
другое, вызывающее ускорение – это сила.
Однако, спор вокруг определения силы не закончен до сих пор – это обусловлено трудностью объединения в одном определении сил, различных по своей природе и характеру проявления.
Слайд 3
В настоящее время различают четыре типа сил или
взаимодействий:
гравитационные;
электромагнитные;
сильные (ответственное
за связь частиц в ядрах) и
слабые (ответственное за распад частиц)
Слайд 4
Гравитационные и электромагнитные силы нельзя свести к другим,
более простым силам, поэтому их называют фундаментальными.
Законы фундаментальных сил
просты и выражаются точными формулами. Для примера можно привести формулу гравитационной силы взаимодействия двух материальных точек, имеющих массы и
где r – расстояние между точками,
γ – гравитационная постоянная.
Слайд 5
В качестве второго примера можно привести формулу для
определения силы электростатического взаимодействия двух точечных зарядов
и
(4.1.2)
где – коэффициент пропорциональности, зависящий от выбора системы единиц.
Как видно, формулы для фундаментальных сил являются простыми и точными.
Для других сил, например, для упругих сил и сил трения можно получить лишь приближенные, эмпирические формулы.
Слайд 6
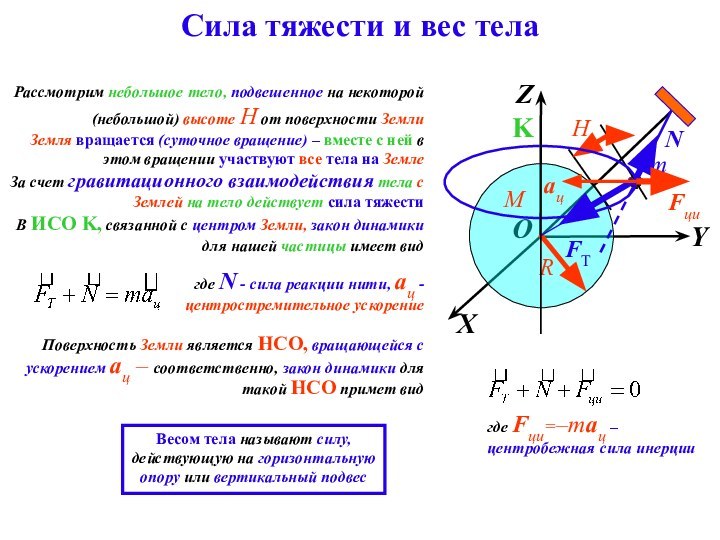
Сила тяжести и вес тела
Рассмотрим небольшое тело, подвешенное
на некоторой (небольшой) высоте H от поверхности Земли
Земля вращается
(суточное вращение) – вместе с ней в этом вращении участвуют все тела на Земле
За счет гравитационного взаимодействия тела с Землей на тело действует сила тяжести
В ИСО K, связанной с центром Земли, закон динамики для нашей частицы имеет вид
X
Y
Z
K
m
O
R
FT
M
H
N
aц
где N - сила реакции нити, aц - центростремительное ускорение
Поверхность Земли является НСО, вращающейся с ускорением aц – соответственно, закон динамики для такой НСО примет вид
где Fци=–maц – центробежная сила инерции
Fци
Весом тела называют силу, действующую на горизонтальную опору или вертикальный подвес
Слайд 7
Сила тяжести и вес тела
Одна из фундаментальных
сил – сила гравитации проявляется на Земле в виде
силы тяжести – силы, с которой все тела притягиваются к Земле.
Вблизи поверхности Земли все тела падают с одинаковым ускорением – ускорением свободного падения g, (вспомним школьный опыт – «трубка Ньютона»). Отсюда вытекает, что в системе отсчета, связанной с Землей, на всякое тело действует сила тяжести
Слайд 8
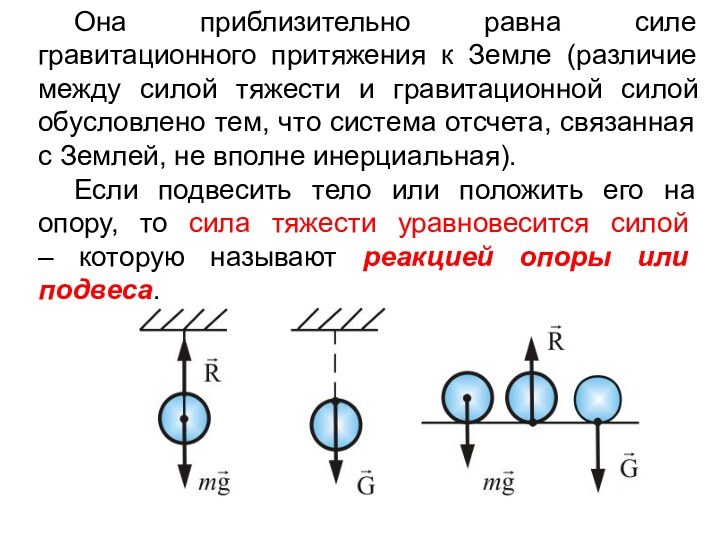
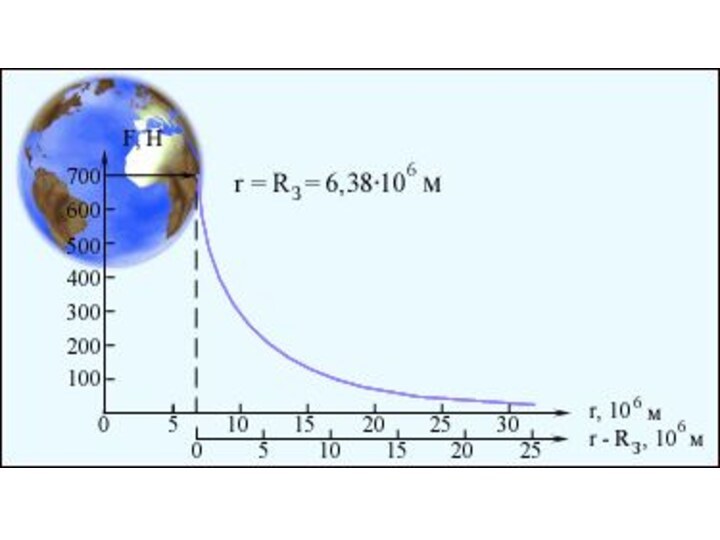
Она приблизительно равна силе гравитационного притяжения к Земле
(различие между силой тяжести и гравитационной силой обусловлено тем,
что система отсчета, связанная с Землей, не вполне инерциальная).
Если подвесить тело или положить его на опору, то сила тяжести уравновесится силой – которую называют реакцией опоры или подвеса.
Слайд 9
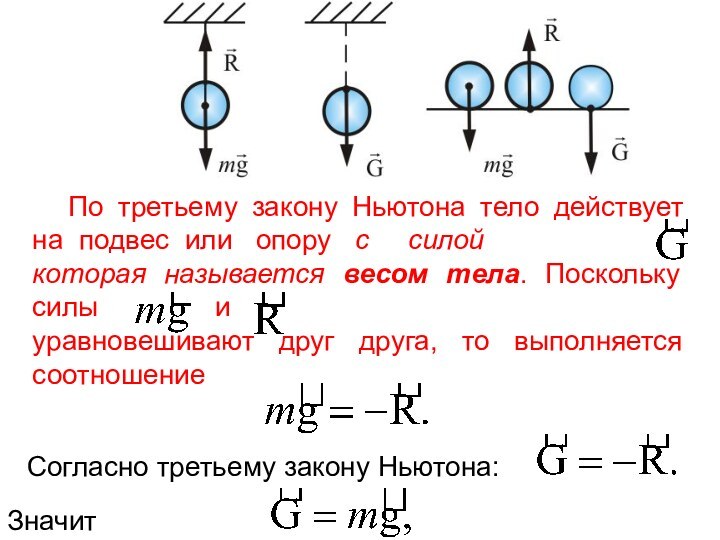
По третьему закону Ньютона тело действует на подвес
или опору с силой
которая
называется весом тела. Поскольку силы и
уравновешивают друг друга, то выполняется соотношение
Согласно третьему закону Ньютона:
Значит
Слайд 11
Вес и сила тяжести равны друг другу, но
приложены к разным точкам: вес к подвесу или опоре,
сила тяжести – к самому телу. Это равенство справедливо, если подвес (опора) и тело покоятся относительно Земли (или двигаются равномерно, прямолинейно). Если имеет место движение с ускорением, то справедливо соотношение:
Слайд 12
и если наоборот, то
Если же
тело движется с ускорением то
– т.е. наступает состояние невесомости.
Пример: космический корабль на орбите.
Вес тела может быть больше или меньше силы тяжести: если g и a направлены в одну сторону (тело движется вниз или падает), то
Слайд 13
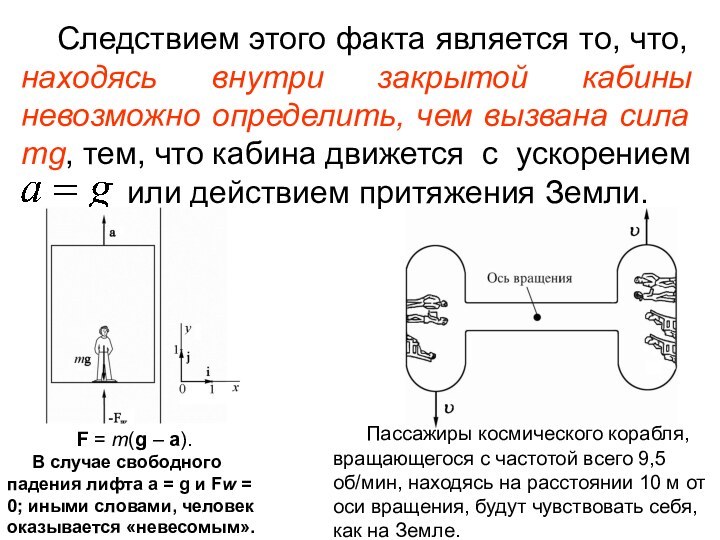
Следствием этого факта является то, что, находясь внутри
закрытой кабины невозможно определить, чем вызвана сила mg, тем,
что кабина движется с ускорением
или действием притяжения Земли.
F = m(g – а).
В случае свободного падения лифта а = g и Fw = 0; иными словами, человек оказывается «невесомым».
Пассажиры космического корабля, вращающегося с частотой всего 9,5 об/мин, находясь на расстоянии 10 м от оси вращения, будут чувствовать себя, как на Земле.
Слайд 15
Упругие силы
Электромагнитные силы проявляют себя как упругие
силы и силы трения.
Под действием внешних сил возникают деформации
(т.е. изменение размеров и формы) тел. Если после прекращения действия внешних сил восстанавливаются прежние форма и размеры тела, то деформация называется упругой. Деформация имеет упругий характер в случае, если внешняя сила не превосходит определенного значения, которая называется пределом упругости.
Слайд 16
При превышении этого предела деформация становится пластичной или
неупругой, т.е. первоначальные размеры и форма тела полностью не
восстанавливается.
Рассмотрим упругие деформации.
В деформированном теле возникают упругие силы, уравновешивающие внешние силы. Под действием внешней силы – Fвн. пружина получает удлинение x, в результате в ней возникает упругая сила – Fупр., уравновешивающая Fвн..
Слайд 17
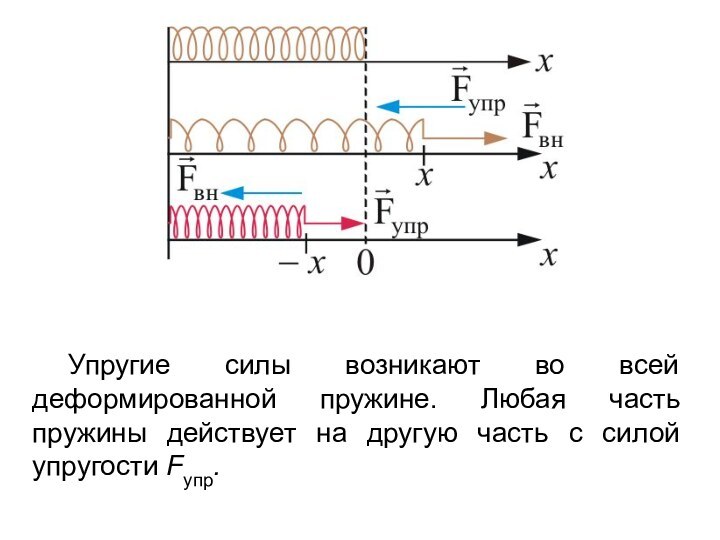
Упругие силы возникают во всей деформированной пружине. Любая
часть пружины действует на другую часть с силой упругости
Fупр.
Слайд 18
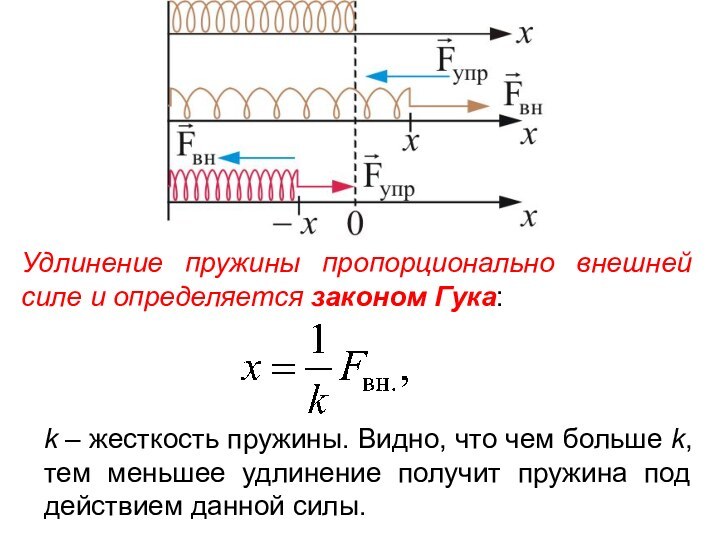
Удлинение пружины пропорционально внешней силе и определяется законом
Гука:
k – жесткость пружины. Видно, что чем больше k, тем меньшее удлинение получит пружина под действием данной силы.
Слайд 19
Его работы относятся к теплоте, упругости, оптике, небесной
механике. Установил постоянные точки термометра – точку таяния льда,
точку кипения воды. Усовершенствовал микроскоп, что позволило ему осуществить ряд микроскопических исследований, в частности наблюдать тонкие слои в световых пучках, изучать строение растений. Положил начало физической оптике.
Гук Роберт (1635 – 1703) знаменитый английский физик, сделавший множество изобретений и открытий в области механики, термодинамики, оптики
Слайд 20
Так как упругая сила отличается от
внешней только
знаком, т.е.
то закон Гука можно записать в виде:
отсюда
Слайд 21
Тогда полная работа, которая совершена пружиной, равна:
Потенциальная
энергия упругой пружины равна работе, совершенной над пружиной.
Так как
сила не постоянна, то элементарная работа равна
Слайд 22
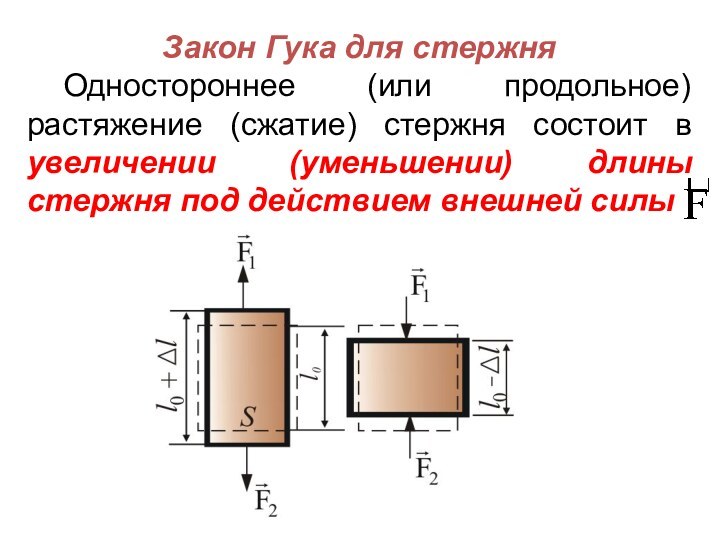
Закон Гука для стержня
Одностороннее (или продольное) растяжение (сжатие)
стержня состоит в увеличении (уменьшении) длины стержня под действием
внешней силы
Слайд 23
Такая деформация приводит к возникновению в стержне упругих
сил, которые принято характеризовать напряжением σ:
Здесь
– площадь поперечного
сечения стержня, d – его диаметр.
В случае растяжения σ считается положительной, а в случае сжатия – отрицательной. Опыт показывает, что приращение длины стержня l пропорционально напряжению σ:
Слайд 24
Коэффициент пропорциональности k, как и в случае пружины,
зависит от свойств материала и длины стержня.
Доказано, что
где Е –
величина, характеризующая упругие свойства материала стержня – модуль Юнга.
Е измеряется в Н/м2 или в Па.
–
относительное
приращение длины, получим:
Закон Гука для стержня: относительное приращение длины стержня прямо пропорционально напряжению и обратно пропорционально модулю Юнга.
приращение длины:
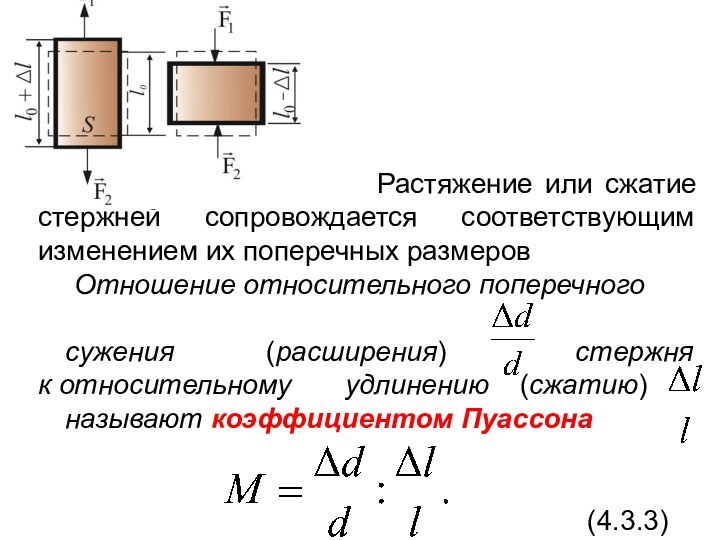
Растяжение или сжатие стержней
сопровождается соответствующим изменением их поперечных размеров
Отношение относительного поперечного
сужения (расширения) стержня к относительному удлинению (сжатию)
называют коэффициентом Пуассона
(4.3.3)
Слайд 27
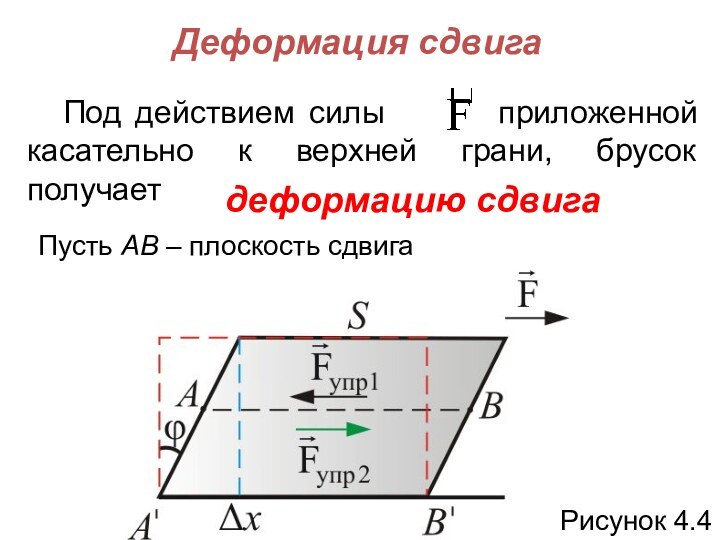
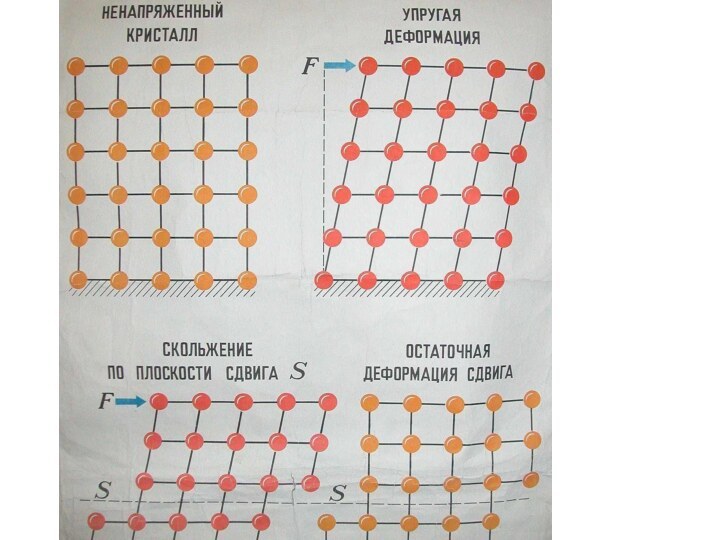
Деформация сдвига
Под действием силы приложенной
касательно к верхней грани, брусок
получает
деформацию сдвига
Пусть АВ – плоскость сдвига
Рисунок 4.4
Слайд 29
Силы трения
Трение подразделяется на внешнее и внутреннее.
Внешнее трение
возникает при относительном перемещении двух соприкасающихся твердых тел (трение
скольжения или трение покоя).
Внутреннее трение наблюдается при относительном перемещении частей одного и того же сплошного тела (например, жидкость или газ).
Различают сухое и жидкое (или вязкое) трение.
Слайд 30
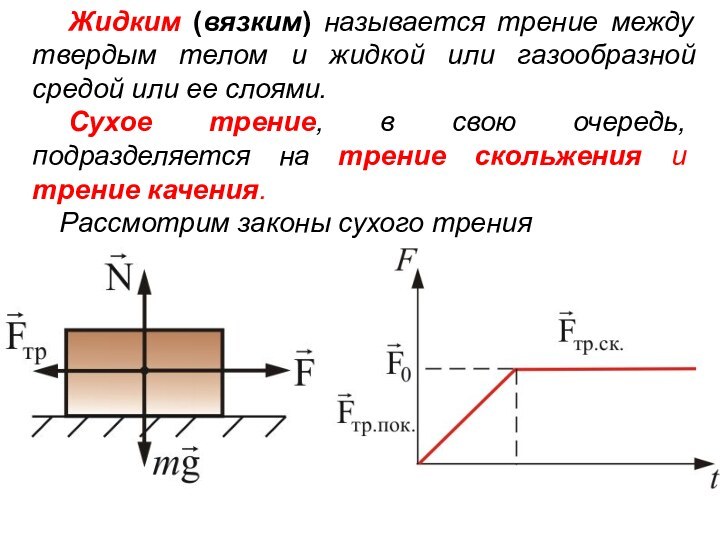
Жидким (вязким) называется трение между твердым телом и
жидкой или газообразной средой или ее слоями.
Сухое трение, в
свою очередь, подразделяется на трение скольжения и трение качения.
Рассмотрим законы сухого трения
Слайд 31
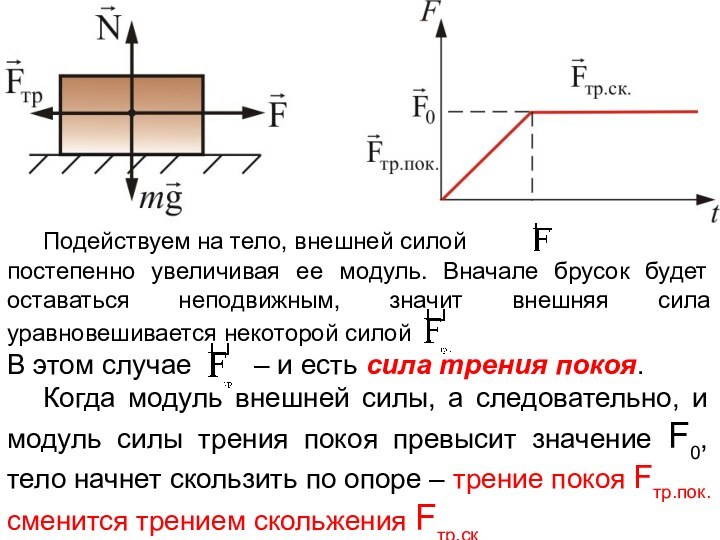
Подействуем на тело, внешней силой
постепенно увеличивая ее модуль. Вначале брусок будет оставаться неподвижным,
значит внешняя сила уравновешивается некоторой силой
В этом случае – и есть сила трения покоя.
Когда модуль внешней силы, а следовательно, и модуль силы трения покоя превысит значение F0, тело начнет скользить по опоре – трение покоя Fтр.пок. сменится трением скольжения Fтр.ск
Слайд 32
Установлено, что максимальная сила трения покоя не зависит
от площади соприкосновения тел и приблизительно пропорциональна модулю силы
нормального давления N
μ0 – коэффициент трения покоя – зависит от природы и состояния трущихся поверхностей.
Аналогично и для силы трения скольжения:
.
Трение качения возникает между шарообразным телом и поверхностью, по которой оно катится.
Слайд 33
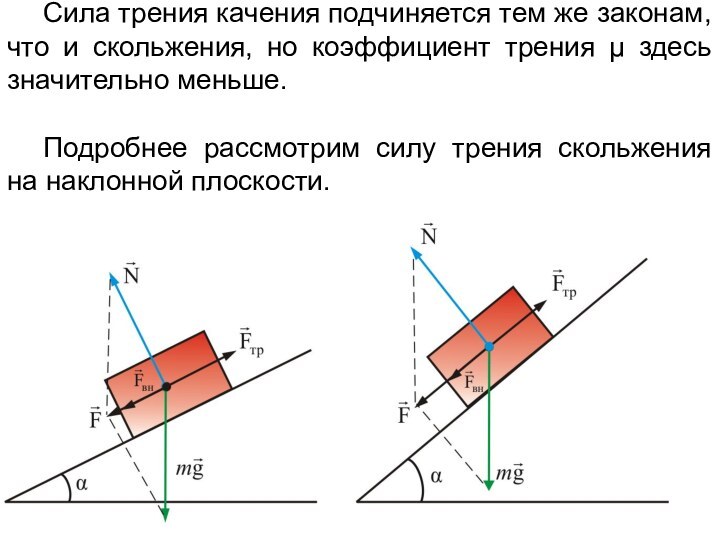
Сила трения качения подчиняется тем же законам, что
и скольжения, но коэффициент трения μ здесь значительно меньше.
Подробнее
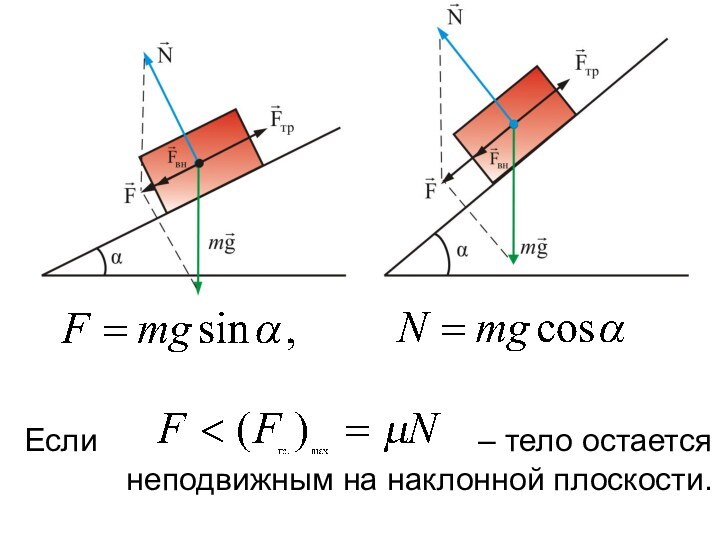
рассмотрим силу трения скольжения на наклонной плоскости.
– тело остается неподвижным на наклонной плоскости.
Слайд 35
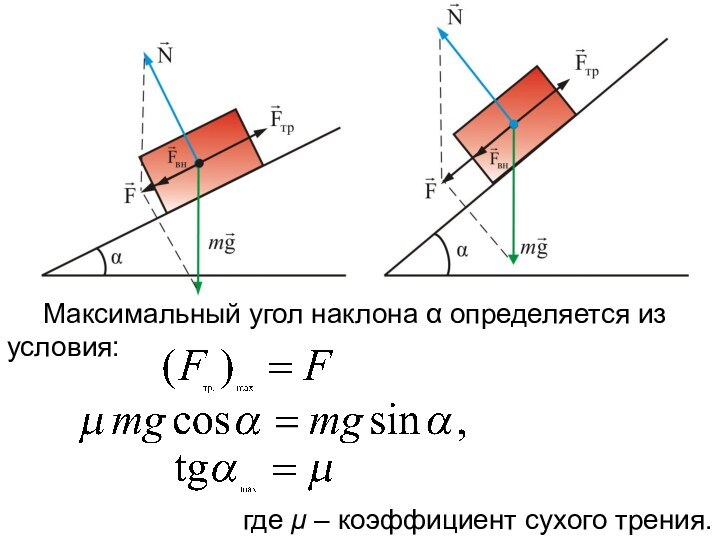
Максимальный угол наклона α определяется из условия:
где μ – коэффициент сухого трения.
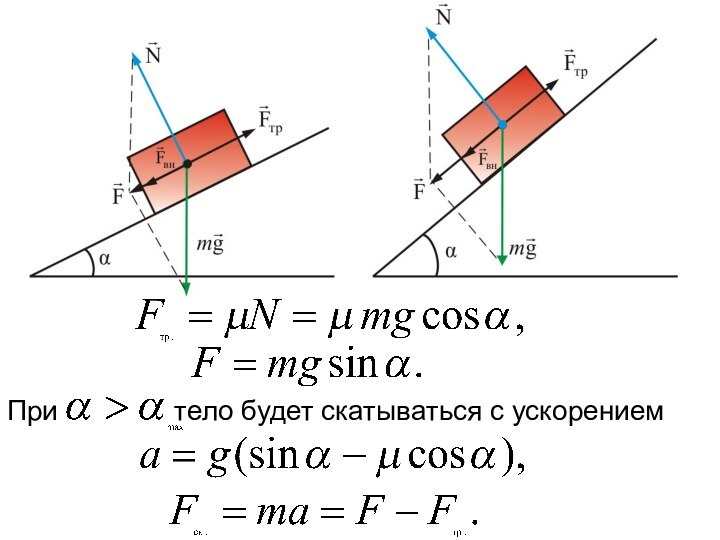
тело будет скатываться с ускорением
Слайд 37
Силы инерции
4.5.1. Уравнение Ньютона для неинерциальных систем
отсчета
Законы
инерции выполняются в инерциальной системе отсчета. А как описать
движение тела в неинерциальной системе?
Рассмотрим пример: вы стоите в троллейбусе спокойно. Вдруг троллейбус резко трогается, и вы невольно отклонитесь назад. Что произошло? Кто вас толкнул?
Слайд 38
С точки зрения наблюдателя на Земле (в инерциальной
системе отсчета), в тот момент, когда троллейбус тронулся, вы
остались стоять на месте – в соответствии с первым законом Ньютона.
С точки зрения сидящего в троллейбусе – вы начали двигаться назад, как если бы кто-нибудь вас толкнул. На самом деле, никто не толкнул, просто ваши ноги, связанные силами трения с троллейбусом «поехали» вперед из-под вас и вам пришлось падать назад.
Можно описать ваше движение в инерционной системе отсчета. Но это не всегда просто, так как обязательно нужно вводить силы, действующие со стороны связей.
Слайд 39
Они могут быть самыми разными и ведут себя
по разному – нет единого подхода к их описанию.
Можно
и в неинерциальной системе воспользоваться законами Ньютона, если ввести силы инерции. Они фиктивны. Нет тела или поля под действием которого вы начали двигаться в троллейбусе. Силы инерции вводят специально, чтобы воспользоваться уравнениями Ньютона в неинерциальной системе.
Силы инерции обусловлены не взаимодействием тел, а свойствами самих неинерциальных систем отсчета. На силы инерции законы Ньютона не распространяются.
Слайд 40
Найдем количественное выражение для силы инерции при поступательном
движении неинерциальной системы отсчета.
Введем обозначения:
– ускорение
тела относительно неинерциальной системы;
– ускорение неинерциальной системы относительно инерциальной (относительно Земли).
Тогда ускорение тела относительно инерциальной системы:
(4.5.1)
Слайд 41
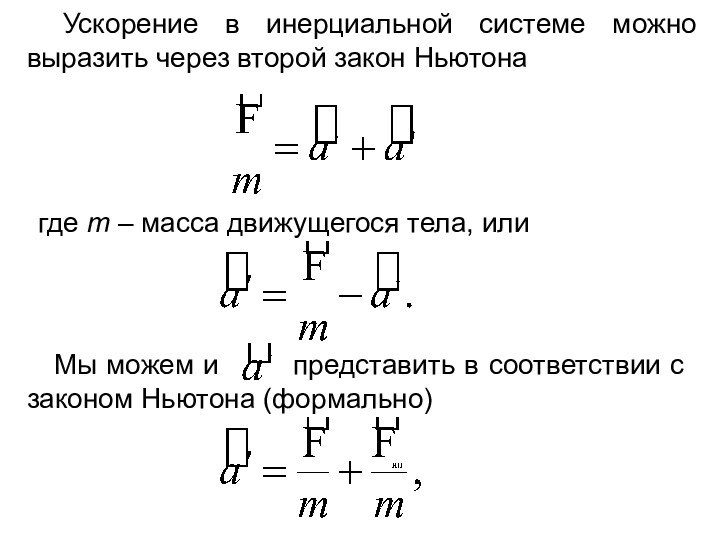
Ускорение в инерциальной системе можно выразить через второй
закон Ньютона
где m – масса движущегося тела, или
Мы можем
и представить в соответствии с законом Ньютона (формально)
направленная в сторону, противоположную ускорению неинерциальной системы.
тогда получим
–
уравнение Ньютона для неинерциальной системы отсчета.
Здесь – фиктивная сила, обусловленная свойствами системы отсчета, необходимая нам для того, чтобы иметь возможность описывать движения тел в неинерциальных системах отсчета с помощью уравнений Ньютона.
Слайд 43
Силы инерции неинвариантны относительно перехода из одной системы
отсчета в другую. Они не подчиняются закону действия и
противодействия. Движения тела под действием сил инерции аналогично движению во внешнем силовом поле. Силы инерции всегда являются внешним по отношению к любому движению системы материальных тел.
Слайд 44
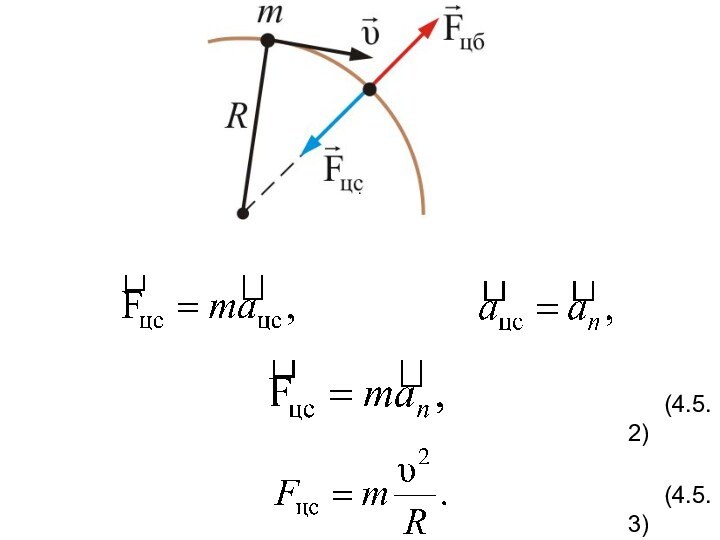
Центростремительная и центробежная силы
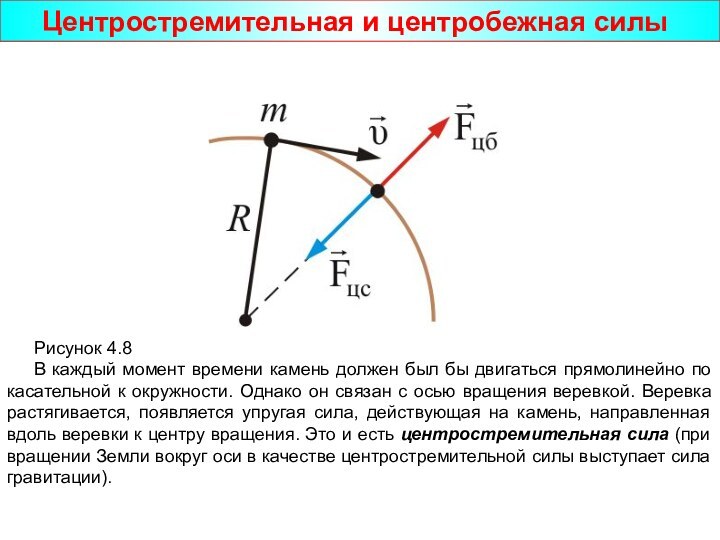
Рисунок 4.8
В каждый момент
времени камень должен был бы двигаться прямолинейно по касательной
к окружности. Однако он связан с осью вращения веревкой. Веревка растягивается, появляется упругая сила, действующая на камень, направленная вдоль веревки к центру вращения. Это и есть центростремительная сила (при вращении Земли вокруг оси в качестве центростремительной силы выступает сила гравитации).
Слайд 46
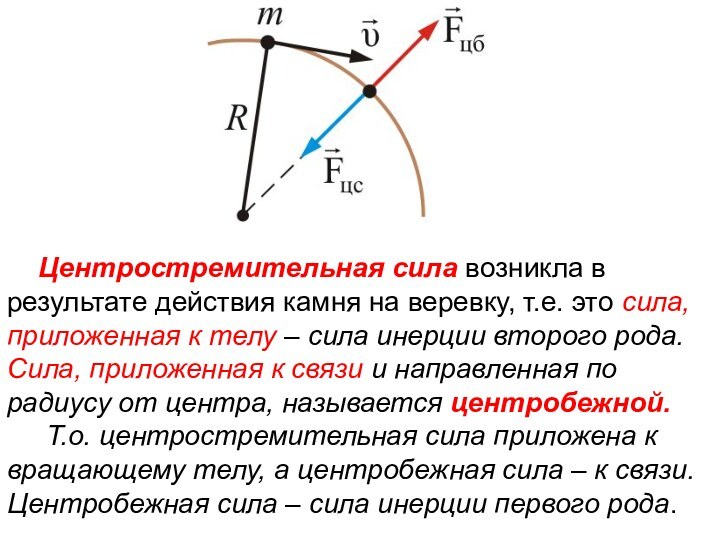
Центростремительная сила возникла в результате действия
камня на веревку, т.е. это сила, приложенная к телу
– сила инерции второго рода.
Сила, приложенная к связи и направленная по радиусу от центра, называется центробежной.
Т.о. центростремительная сила приложена к вращающему телу, а центробежная сила – к связи.
Центробежная сила – сила инерции первого рода.
Слайд 47
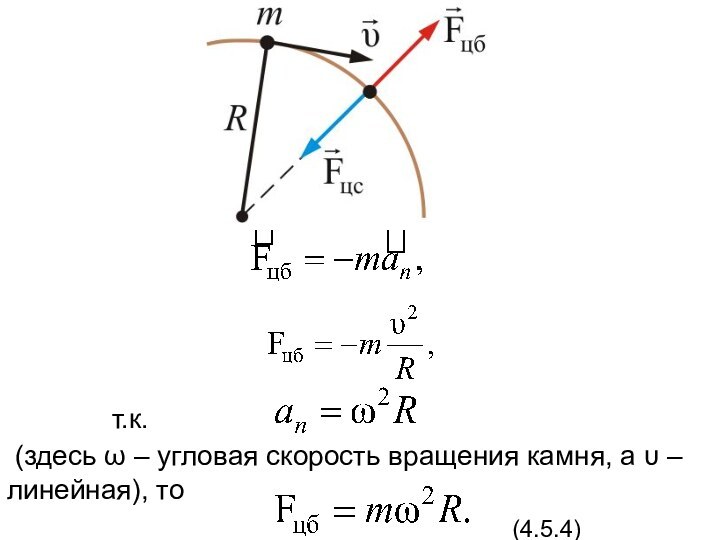
т.к.
(здесь ω – угловая скорость вращения
камня, а υ – линейная), то
(4.5.4)
Слайд 48
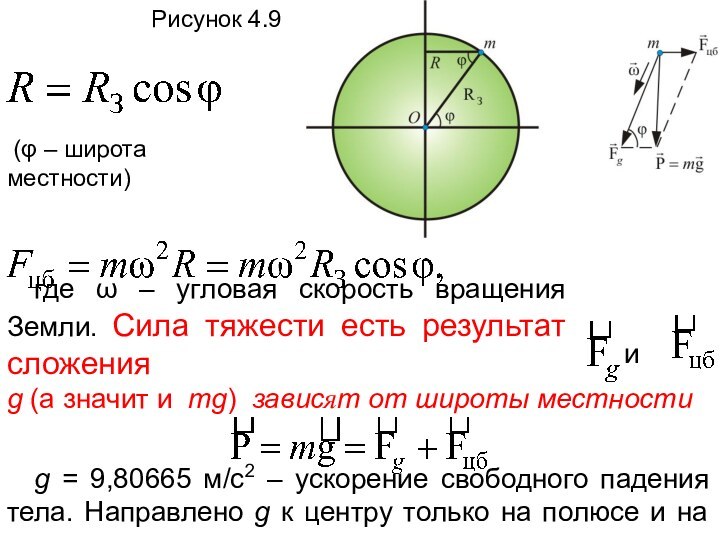
Рисунок 4.9
(φ – широта местности)
где ω
– угловая скорость вращения Земли. Сила тяжести есть результат
сложения
и
g (а значит и mg) зависят от широты местности
g = 9,80665 м/с2 – ускорение свободного падения тела. Направлено g к центру только на полюсе и на экваторе.
Слайд 49
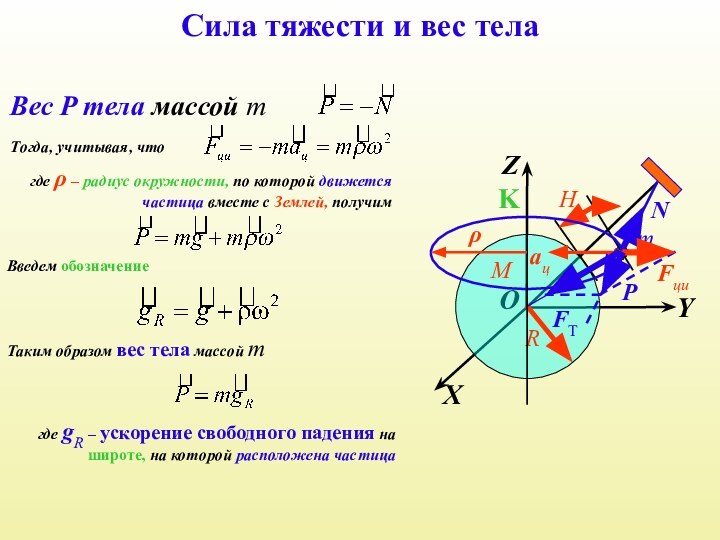
Сила тяжести и вес тела
Вес P тела массой
m
X
Y
Z
K
m
O
R
FT
M
H
N
aц
Fци
Тогда, учитывая, что
ρ
где ρ – радиус окружности, по которой
движется частица вместе с Землей, получим
Введем обозначение
Таким образом вес тела массой m
где gR – ускорение свободного падения на широте, на которой расположена частица
P
Слайд 50
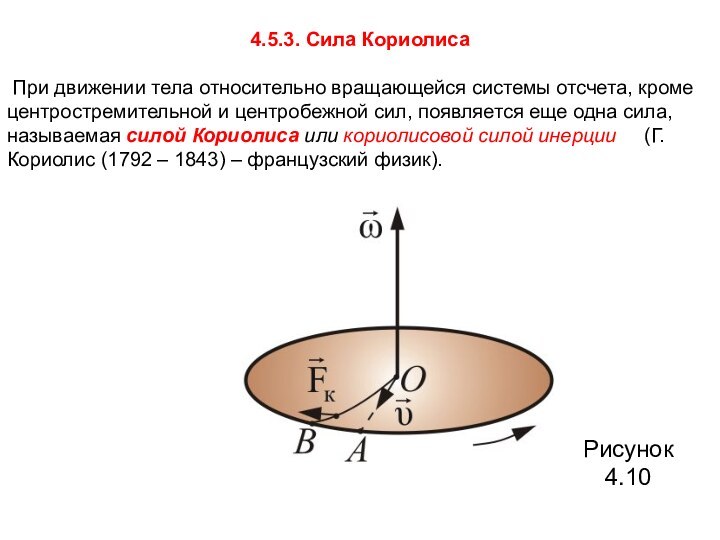
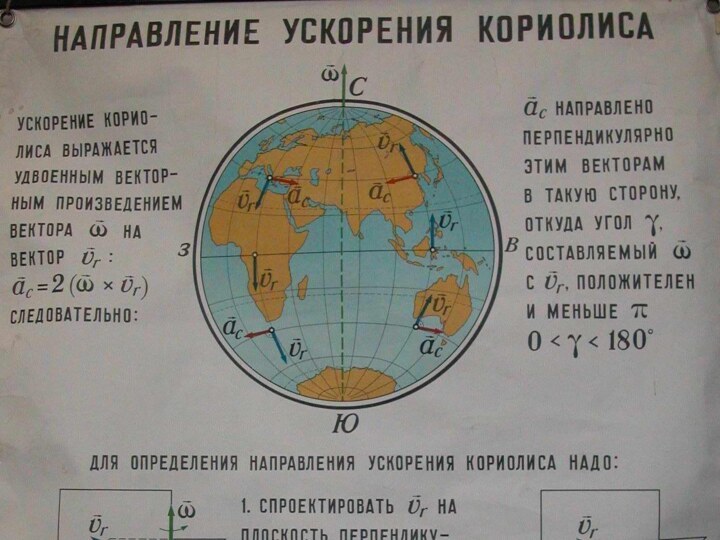
4.5.3. Сила Кориолиса
При движении тела относительно вращающейся
системы отсчета, кроме центростремительной и центробежной сил, появляется еще
одна сила, называемая силой Кориолиса или кориолисовой силой инерции (Г. Кориолис (1792 – 1843) – французский физик).
Рисунок 4.10
Слайд 51
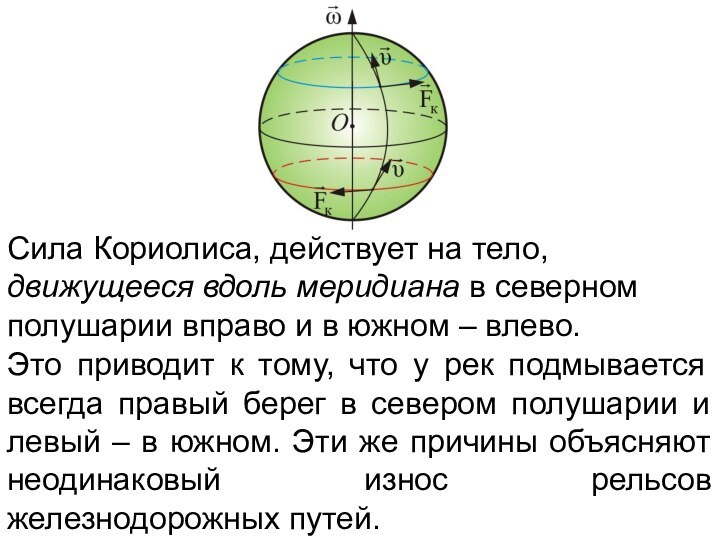
Это приводит к тому, что у рек подмывается
всегда правый берег в севером полушарии и левый –
в южном. Эти же причины объясняют неодинаковый износ рельсов железнодорожных путей.
Сила Кориолиса, действует на тело, движущееся вдоль меридиана в северном полушарии вправо и в южном – влево.
Слайд 52
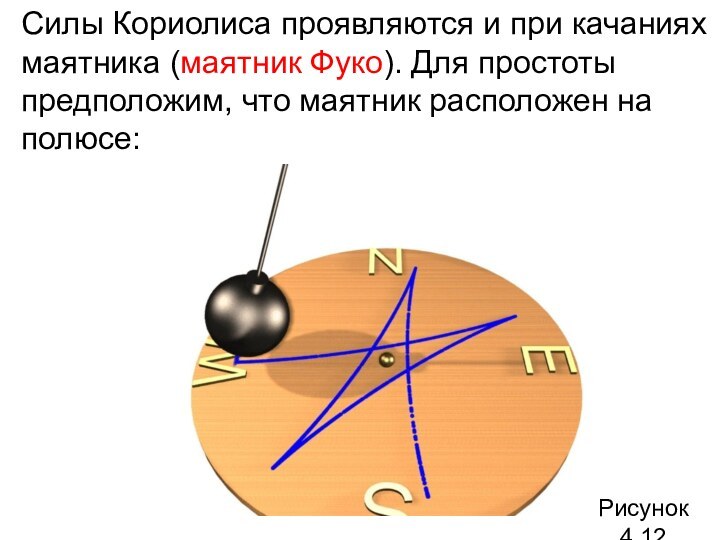
Силы Кориолиса проявляются и при качаниях маятника (маятник
Фуко). Для простоты предположим, что маятник расположен на полюсе:
Рисунок
4.12