Презентация на тему Случайные величины: законы распределения

величина, которая в результате испытания примет одно и только

одно возможное значение, наперед не известное и зависящее от случайных причин, которые
заранее не могут быть учтены.

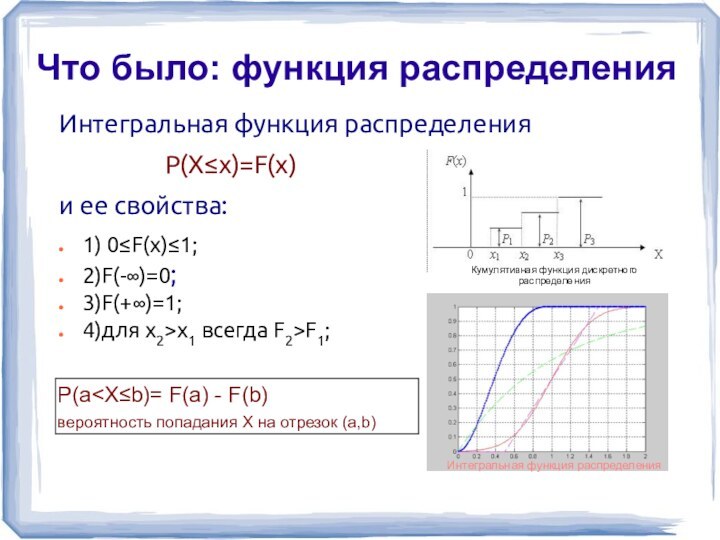
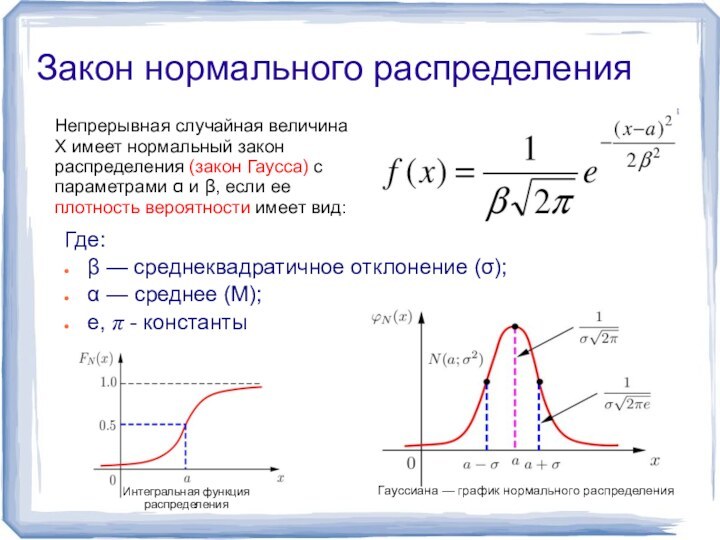
Функцией распределения случайной величины X называется функция F (x), выражающая для каждого x вероятность того, что случайная величина X примет значение, меньшее x
F (x) = P (X < x).

P(X≤x)=F(x)
и

ее свойства:
1) 0≤F(x)≤1;
2)F(-∞)=0;
3)F(+∞)=1;
4)для x2>x1 всегда F2>F1;

Кумулятивная функция дискретного распределения

Интегральная функция распределения

для непрерывных случайных величин!
lim∆x->0 ∆F/∆x=F'(x)= f(x) - плотность

вероятности
И наоборот: -∞∫х f(x) dx=F(x)
Свойства: 1) f(x)≥0
2) ∫f(x)dx=1

Интеграл как площадь

Функция плотности вероятности

М[x]=
Дисперсия
D[x]=
Мода (значение

с наибольшей вероятностью)
Мо=Xi | p(xi)=pmax
Медиана

Непрерывная случайная величина
Математическое ожидание:
M[X]=
Дисперсия
D[X]=
Мода (значение с наибольшей плотностью вероятности)
Мо=xi | f(xi)=max
Медиана

что такое интегральная (кумулятивная) функция распределения

и распределение плотности вероятности;
вероятность попадания Х на отрезок (а,b);
как описать распределение F(x).

Не знаем, какие бывают F(x)

распределения на (а,b), если ее плотность вероятности постоянна на

этом отрезке и равна 0 вне его.
Функция P(XF(x)=0 при x≤a
F(x)=(x-a)/(b-a) при aF(x)=1 при x>b
Математическое ожидание: M[x]=(a+b)/2
Дисперсия: D[x]=(b-a)2/12

График интегральной функции распределения

График плотности вероятности

если ее функция вероятности на всей области определения (a,b)

имеет вид
P(x)=1/n,
где n — число исходов
M[x]=(a+b)/2 - мат.ожидание
D[x]=(n2-1)/12 - дисперсия

График кумулятивной функции

График характеристической функции

по биномиальному закону, если она имеет значения {0...n}, а

вероятность Х=m
P(X=m)=

Биномиальное распределение описывает вероятность m успехов при n возможных исходов
M[X]=n*p - мат. ожидание
D[X]=n*p*q - дисперсия,
где p - вероятность успеха, q - вероятность неуспеха

Кумулятивная функция, F(X

если ее плотность вероятности имеет вид:
f(x)=Cx-α ,

при α=[2,3]
Свойства:
ассиметричное распределение с «тяжелым» хвостом
прямая линия на log-log шкале;
Вид графика не зависит от масштаба (scale invariance)

Принцип Парето: 80/20

M.E.J. Newman. Power laws, Pareto distribution and Zipf's law/ arXiv:cond-mat/0412004

Если индивидуальная изменчивость некоторого свойства есть следствие действия множества

причин, то распределение частот для всего многообразия проявлений этого свойства в генеральной совокупности соответствует кривой нормального распределения

распределения
Где:
β — среднеквадратичное отклонение (σ);
α — среднее (М);
e, π

- константы

Непрерывная случайная величина X имеет нормальный закон распределения (закон Гаусса) с параметрами α и β, если ее плотность вероятности имеет вид:

возможных значений




Вероятность попадания нормально распределенной
случайной величины на

отрезок(с,d)

Табличная функция Лапласа

в рамках M+/-3σ)
Распределение симметрично (А=0), эксцесс, т.е. мера остроты

пика или Е = 0
Мода, медиана и среднее совпадают
Значения, лежащие на равном расстоянии от M (среднего), будут иметь равную частоту в репрезентативной выборке

человек) ;
W-критерий Шапиро-Уилка (N > 8 человек);
Критерий ассиметрии и

эксцесса
См. ГОСТ Р ИСО 5479—2002

и стандартное отклонение (σ).
2. Рассчитать показатели асимметрии и эксцесса.
А=

Е= -3

3. Рассчитать критические значения А и Е
А Е

4. Если А