Слайд 2
Историческая справка.
Статика - самый старый раздел механики;
некоторые из ее принципов были известны уже древним египтянам
и вавилонянам, о чем свидетельствуют построенные ими пирамиды и храмы. Среди первых создателей теоретической статики был Архимед (ок. 287-212 до н.э.), который разработал теорию рычага и сформулировал основной закон гидростатики. Родоначальником современной статики стал голландец С.Стевин (1548-1620), который в 1586 сформулировал закон сложения сил, или правило параллелограмма, и применил его в решении ряда задач.
Симон Стевин стал известен прежде всего своей книгой «Десятая» (De Thiende), изданной на фламандском и французском языках в 1585 г. Именно после неё в Европе началось широкое использование десятичных дробей.
Слайд 3
Около 1600 г. Стевин продемонстрировал согражданам своё изобретение — сухопутную
парусную яхту на колёсах, и прокатил на ней принца
вдоль побережья быстрее, чем на лошади.
Помимо всего перечисленного, Стевин писал труды по механике, геометрии, теории музыки, изобрёл двойную бухгалтерскую регистрацию (дебет/кредит). В 1590 году составил таблицы, в которых было указано время наступления приливов в любом месте в зависимости от положения Луны.
«Тело на наклонной плоскости удерживается силой, которая ... по величине во столько раз меньше веса этого тела, во сколько раз длина наклонной плоскости больше ее высоты».
Слайд 4
Определения систем сил
Системой сил называется группа сил, которые

действуют на рассматриваемое тело или (в общем случае) на
точки механической системы. Если линии действия всех сил лежат в одной плоскости, то система сил называется плоской, а если эти линии действия не лежат в одной плоскости, - то система сил называется пространственной.
Системой сил, эквивалентной нулю (или уравновешенной системой сил) называется такая система сил, действие которой на твердое тело или материальную точку, находящиеся в покое или движущиеся по инерции, не приводит к изменению состояния покоя или движения по инерции этого тела или материальной точки.
Две системы сил называются эквивалентными, если их действие по отдельности на одно и то же твердое тело или материальную точку одинаково при прочих равных условиях.
Уравновешивающей силой рассматриваемой системы сил называется сила, добавление которой к заданной системе сил дает новую систему сил, эквивалентную нулю. Уравновешивающая сила равна по модулю равнодействующей и противоположна ей по направлению.
Слайд 5
Свободным твердым телом называется тело, имеющее возможность получать
любое движение из данного положения, для чего необходимо приложить
соответствующую силу.
При решении большинства задач механики приходится иметь дело с телами несвободными, т.е. лишенными возможности перемещаться в направлении действия приложенных к ним активных сил. Тела, ограничивающие движение рассматриваемого тела, называются связями. Сила, с которой связь действует на тело, препятствуя его перемещению в том или ином направлении называется силой реакции (противодействия) этой связи или просто реакцией связи.
Две основные задачи статики.
1. Задача о приведении системы сил: заключается в замене данной стстемы сил другой, наиболее простой, ей эквивалентной.
2. Задача о равновесии состоит в определении условий, при которых система сил приложенная к телу будет уравновешенной системой.
Слайд 6
Аксиома 1. Если на свободное абсолютно твердое тело
действуют две силы, то тело может находится в равновесии
только тогда, когда эти силы равны по модулю и направлены вдоль одной прямой в противоположные стороны:
F1 = - F2.
Система сил F1 и F2 называется уравновешивающейся, или эквивалентной нулю: F1+ F2 = 0.
Аксиома 2. Действие данной системы сил на абсолютно твердое тело не изменится, если к ней добавить или от нее отнять уравновешенную систему сил.
Следствие. Не нарушая состояния твердого тела, силу можно переносить по линии ее действия в любую точку тела
Слайд 7
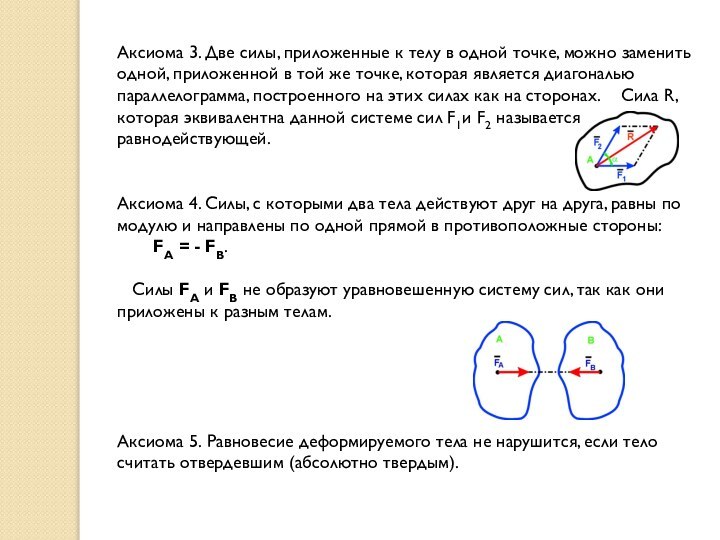
Аксиома 3. Две силы, приложенные к телу в
одной точке, можно заменить одной, приложенной в той же
точке, которая является диагональю параллелограмма, построенного на этих силах как на сторонах. Сила R, которая эквивалентна данной системе сил F1и F2 называется равнодействующей.
Аксиома 4. Силы, с которыми два тела действуют друг на друга, равны по модулю и направлены по одной прямой в противоположные стороны:
FA = - FB.
Cилы FA и FB не образуют уравновешенную систему сил, так как они приложены к разным телам.
Аксиома 5. Равновесие деформируемого тела не нарушится, если тело считать отвердевшим (абсолютно твердым).
Слайд 8
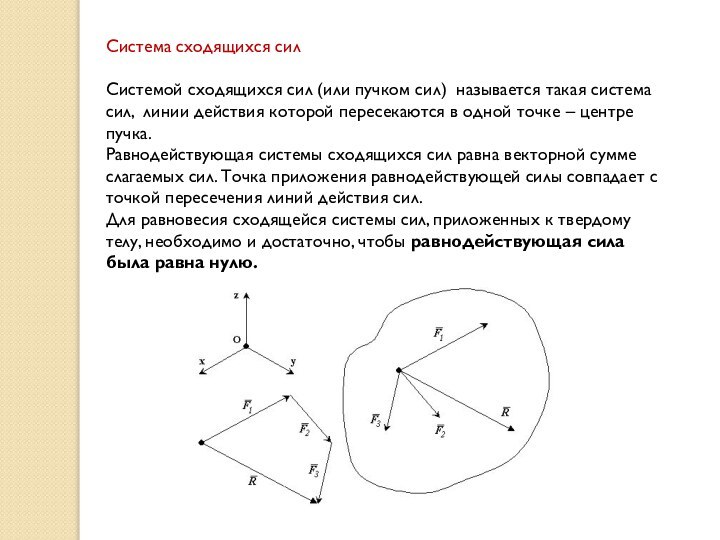
Система сходящихся сил
Системой сходящихся сил (или пучком сил)
называется такая система сил, линии действия которой пересекаются в
одной точке – центре пучка.
Равнодействующая системы сходящихся сил равна векторной сумме слагаемых сил. Точка приложения равнодействующей силы совпадает с точкой пересечения линий действия сил.
Для равновесия сходящейся системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы равнодействующая сила была равна нулю.
Слайд 9
Момент силы относительно точки
Если под действием приложенной силы
твердое тело может совершать вращение вокруг некоторой точки, то
для того, чтобы охарактеризовать вращательный эффект силы, необходимо ввести новое понятие - момент силы относительно точки.
Рассмотрим силу F, приложенную к телу в точке А. Из некоторой точки О опустим перпендикуляр на линию действия силы F.
Плечом h силы относительно точки О называется кратчайшее расстояние между этой точкой и линией действия силы.
Через силу и точку О можно провести плоскость. Сила F пытается вращать тело вокруг оси, которая проходит через точку О и которая перпендикулярна плоскости в которой лежит сила. Точка О называется моментной точкой.
Моментом силы F относительно точки О называется вектор ,
приложенный в этой точке и равный векторному произведению радиус-вектора , соединяющего эту точку с точкой приложения силы, на вектор силы .
Слайд 10
Момент силы F относительно точки О направлен перпендикулярно
плоскости, в которой лежат сила и моментная точка (радиус-вектор),
в том направлении откуда видно стремление силы вращать тело против движения часовой стрелки.
Момент силы относительно точки не меняется от переноса силы вдоль линии ее действия.
Момент силы равен нулю, если линия действия силы проходит через моментную точку.
Слайд 11
Момент силы относительно оси
К твердому телу в точке
А приложена сила F . Проведем в пространстве ось
(например z). На оси z произвольно выберем точку О . Соединим точку О с точкой А радиус-вектором r. Через точку О проведем плоскость П перпендикулярную оси z. Спроектируем точку А и вектора F и r на плоскость П .
Моментом силы F относительно оси z называется вектор, равный моменту проекции силы F на плоскость П относительно точки О пересечения оси z с плоскостью П.
Слайд 12
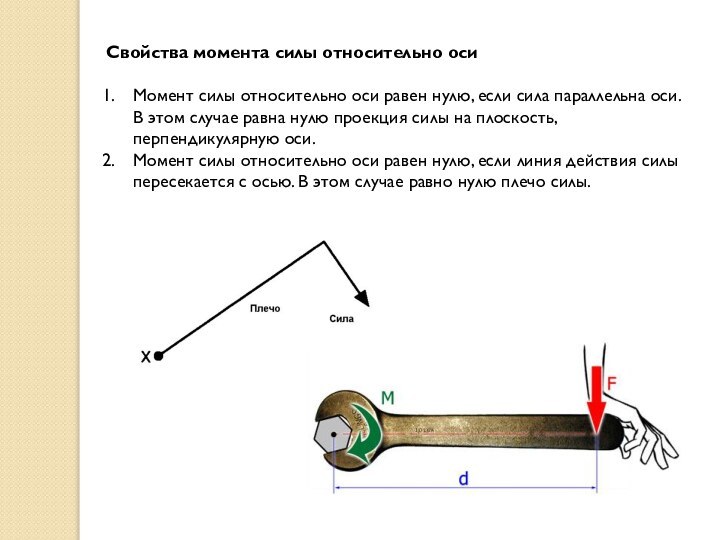
Свойства момента силы относительно оси
Момент силы относительно оси
равен нулю, если сила параллельна оси. В этом случае
равна нулю проекция силы на плоскость, перпендикулярную оси.
Момент силы относительно оси равен нулю, если линия действия силы пересекается с осью. В этом случае равно нулю плечо силы.
Слайд 13
Условия равновесия системы сил.
Векторная форма
Для равновесия произвольной системы
сил, приложенных к твердому телу, необходимо и достаточно, чтобы
равнодействующая системы сил была равна нулю и суммарный момент системы сил относительно любого центра приведения также был равен нулю.
Алгебраическая форма
Для равновесия произвольной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы три суммы проекций всех сил на оси декартовых координат были равны нулю и три суммы моментов всех сил относительно трех осей координат также были равны нулю.
Условия равновесия плоской системы сил
Для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух прямоугольных осей координат, расположенных в плоскости действия сил, были равны нулю и сумма моментов этих сил относительно любой точки, находящейся в плоскости действия сил также была равна нулю.
Слайд 14
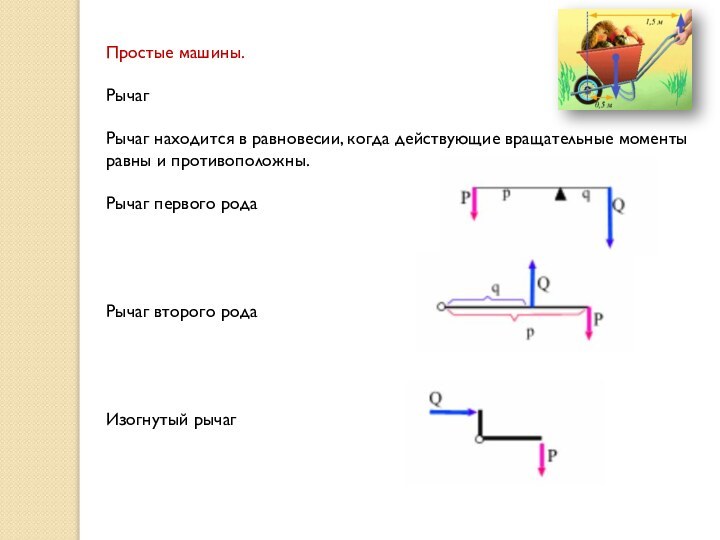
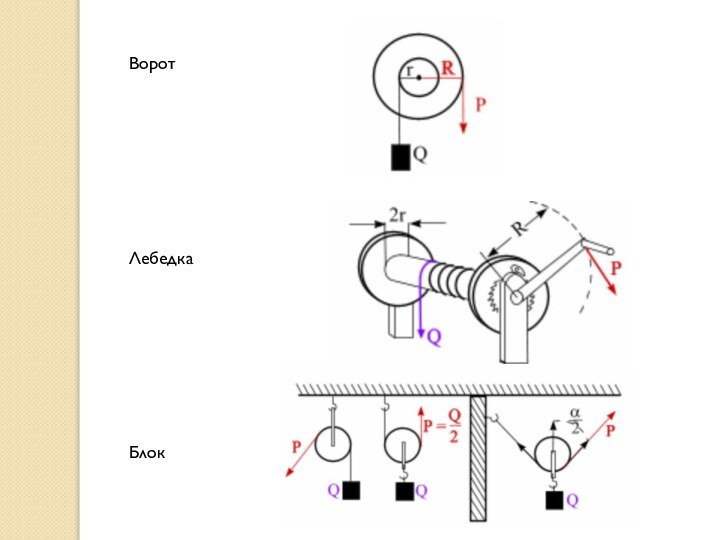
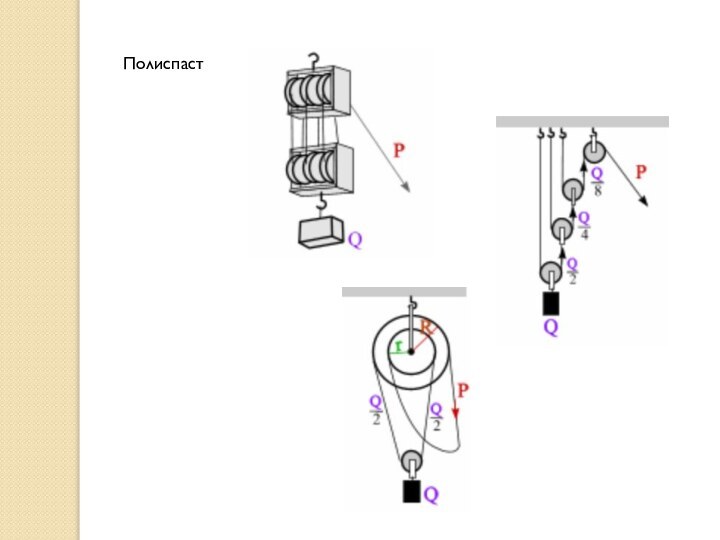
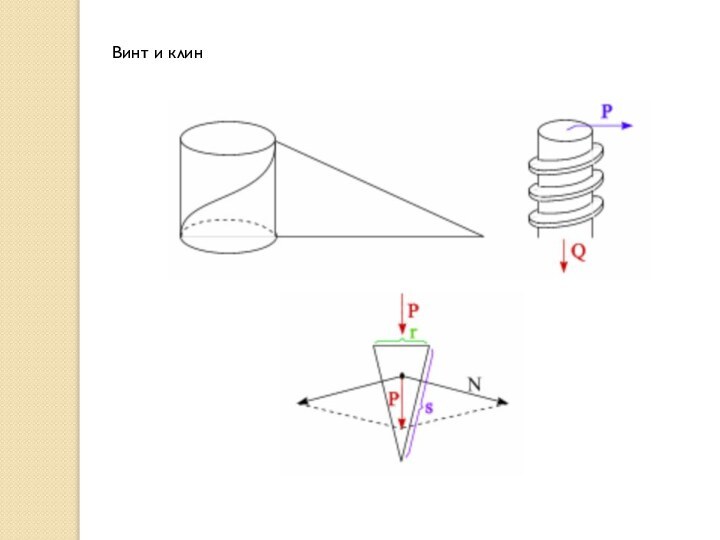
Простые машины.
Рычаг
Рычаг находится в равновесии, когда действующие
вращательные моменты равны и противоположны.
Рычаг первого рода
Рычаг второго
рода
Изогнутый рычаг
Слайд 18
Задача
Лестница длиной 4 м приставлена к идеально гладкой
стене под углом 60° к горизонту. Коэффициент трения между
лестницей и полом равен 0,4. На какую максимальную высоту над полом может подняться по лестнице человек, прежде чем она начнет скользить? Масса лестницы 5 кг, человека 60 кг.
Слайд 19
Решение.
Когда человек поднимется на максимальную высоту, то должно
выполняться равенство моментов сил тяжести человека, лестницы и реакции
гладкой стенки относительно точки вращения B.
mgh/tgα + Mg(L/2)cosα = NALsinα (1)
Так как лестница неподвижна, то выполняется равенство сил
NA = Fmp
Fmp = μNB
NB = mg + Mg.
Тогда
NA = μ(mg + Mg) (2)
Подставим (2) в (1)
mgh/tgα + Mg(L/2)cosα = μ(mg + Mg)Lsinα.
После преобразования
h = μ(m + M)Lsinαtgα/m − MLsinα/(2m).
Подставим численные значения
h = (0,4•(60 + 5)•4•sin60•tg60)/60 − 5•4•sin60°/(2•60) = 2,5 (м)
Слайд 20
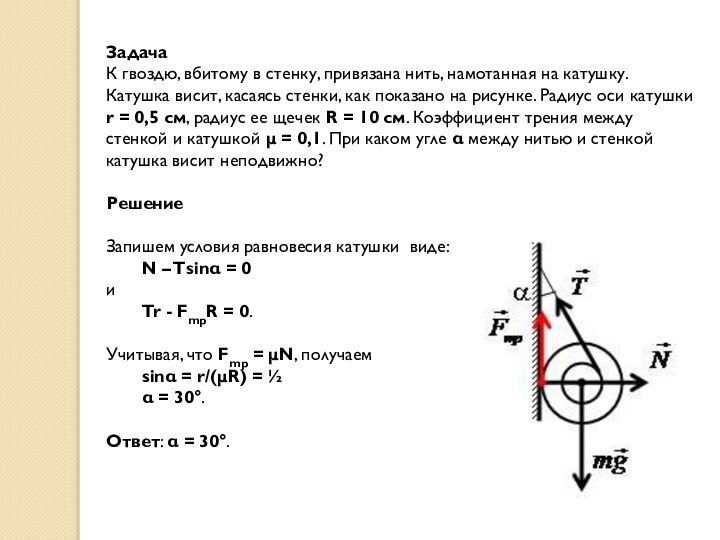
Задача
К гвоздю, вбитому в стенку, привязана нить, намотанная
на катушку. Катушка висит, касаясь стенки, как показано на
рисунке. Радиус оси катушки r = 0,5 см, радиус ее щечек R = 10 см. Коэффициент трения между стенкой и катушкой μ = 0,1. При каком угле α между нитью и стенкой катушка висит неподвижно?
Решение
Запишем условия равновесия катушки виде:
N – Tsinα = 0
и
Tr - FmpR = 0.
Учитывая, что Fmp = μN, получаем
sinα = r/(μR) = ½
α = 30°.
Ответ: α = 30°.
Слайд 21
Задача
На столе лежит однородный стержень массой 6 кг
так, что две трети его длины находятся за краем
стола. Какую силу необходимо приложить к концу стержня для удержания его в горизонтальном положении?
Решение
На стержень действуют три силы: сила тяжести mg, удерживающая сила F и сила реакции опоры N, которая приложена в точке O, так как вначале вращения эта точка является опорой стержня.
Слайд 22
Применим правило моментов относительно оси вращения в точке
O:
Mmg + MF = 0
mgl3 - Fl1 =
0
где Mmg и MF – момент силы тяжести и приложенной силы F, а l3 и l1 – соответствующие плечи сил.
Отсюда имеем
F = mgl3/l1.
Поскольку
l3 = l2 – l4
где l4 = l/2, получаем
l3 = 2l/3 – l/2 = l/6
F = mg/2.
Проводим расчет F = 6•10/2 = 30 H.
Ответ: F = 6•10/2 = 30 H.
Слайд 23
Задача
Невесомый жесткий стержень длиной l свободно лежит на
двух опорах A и B. В точке C, отстоящей
от A на расстоянии a, на стержень действует вертикальная нагрузка F. Найти реакцию опор.
Решение
Поместим начало координат X и Y в точке A и направим их, как показано на рисунке.
Уравнение проекций на ось Y
FA + FB - F = 0.
Уравнение моментов относительно точки A (направление момента, вызывающего вращение по часовой стрелке, принимаем за положительное)
F a – FB l = 0.
Из двух уравнений находим
FB = F a/l
FA = F(l - a)/l.
Ответ: FB = Fa/l; FA = F(l - a)/l.
Слайд 24
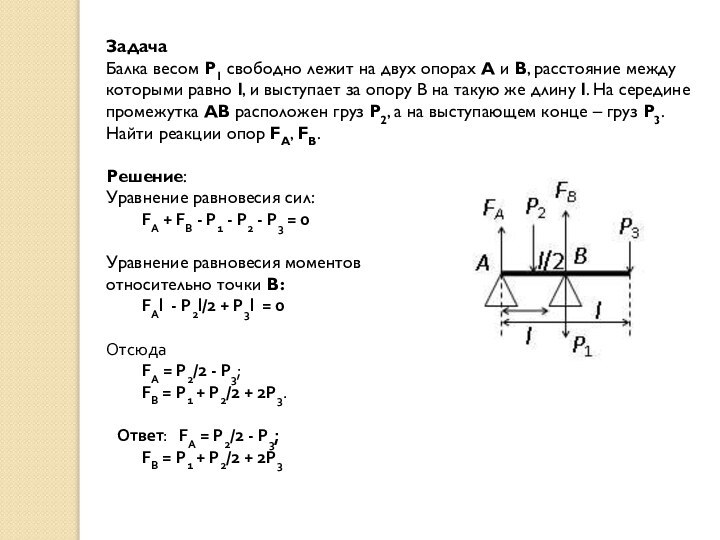
Задача
Балка весом P1 свободно лежит на двух опорах
A и B, расстояние между которыми равно l, и
выступает за опору B на такую же длину l. На середине промежутка AB расположен груз P2, а на выступающем конце – груз P3. Найти реакции опор FA, FB.
Решение:
Уравнение равновесия сил:
FA + FB - P1 - P2 - P3 = 0
Уравнение равновесия моментов
относительно точки B:
FAl - P2l/2 + P3l = 0
Отсюда
FA = P2/2 - P3;
FB = P1 + P2/2 + 2P3.
Ответ: FA = P2/2 - P3;
FB = P1 + P2/2 + 2P3
Слайд 25
Задача
Куб опирается одним ребром на пол, другим –
на гладкую вертикальную стенку. Определить, при каких значениях угла
α возможно равновесие куба. Коэффициент трения куба о пол равен μ, ребро куба равно a.
Решение:
Уравнение проекций на вертикальную ось:
–P + F2 = 0
Уравнение проекций на горизонтальную ось:
F1 – F = 0
Уравнение моментов относительно точки нижней опоры
F1a sinα = Pa(√1/2) cos(π/4 + α)
Кроме того,
F ≤ μF2
Отсюда находим
1 > tgα ≥ 1/(2μ + 1).
Т.к μ > 0, то α всегда меньше π/4, так как при α > π/4 куб опрокинется.
Ответ: 1 > tgα ≥ 1/(2μ + 1)
Слайд 26
Задача
Вертикально вверх произведен выстрел из пушки. Начальная скорость
снаряда vo. В точке максимального подъема снаряд разорвался на
две равные по массе половины. Первая упала вблизи точки выстрела, имея скорость 2vo. Через какое время после выстрела упадет вторая половина? Какую скорость она будет иметь в момент падения?
Решение:
В момент взрыва полный импульс равен нулю:
mv1 + mv2 = 0 или v1 = −v2.
Высота, на которой разорвался снаряд, равна
H = vo2/(2g).
Из закона сохранения энергии для первого осколка получим
mv12/2 + mgH = m(2vo)2/2.
Откуда следует v1 = vo√3, следовательно, v2 = −v1 = −vo√3.
На землю второй осколок упадет с той же скоростью, что и первый осколок. Время его падения t складывается из времени подъема t1 на максимальную высоту и времени падения t2 с этой высоты вниз.
t1 = |v2|/g = vo√3/g, t2 = 2vo/g.
Откуда
t = (vo/g)(2 + √3).
Ответ: t = (vo/g)(2 + √3).
Слайд 27
Задача
Человек, имеющий массу M, прыгает под углом α
к горизонту со скоростью vo. В верхней точке траектории
он бросает со скоростью v1 вертикально вниз груз массой m. На какую общую высоту H подпрыгнул человек?
Решение:
Найдем высоту h верхней точки траектории полета человека
h = vo2sin2α/(2g).
В верхней точке происходит неупругое взаимодействие без участия внешних сил. Поэтому импульс человека компенсируется импульсом груза: Mv = mv1.
Откуда скорость вертикального подъема человека
v = (m/M)v1.
Далее по оси Y человек поднимается, как тело, брошенное вертикально вверх, т. е.
h1 = v2/(2g) = (mv1)2/(M22g).
Общая высота подъема
H = vo2sin2α/(2g) + (mv1)2/(2gM2).
Ответ: H = vo2sin2α/(2g) + (mv1)2/(2gM2).
Слайд 28
Задача
Грузовик едет со скоростью 7 м/с. Мячик массой
0,25 кг, брошенный вдогонку грузовика, ударяется абсолютно упруго в
его задний борт с горизонтальной скоростью 10 м/с. Определите импульс мяча сразу после удара.
Решение:
Относительно грузовика мячик летит со скоростью
vo = v2 − v1.
После упругого отскока мячик полетит с той же скоростью относительно грузовика, но в противоположном направлении. Скорость мячика относительно Земли будет равна сумме противоположно направленных скоростей
v = v1 - vo.
Поэтому для модуля скорости относительно Земли имеем:
v = v1 − vo = v1 − (v2 − v1) = 2v1 − v2.
Для искомого импульса находим:
p = mv = m(2v1 − v2).
Ответ: p = 1,4 кг м/с.
Слайд 29
Задача
Тело брошено вертикально вверх с начальной скоростью 20
м/с. Пренебрегая сопротивлением воздуха, определить, на какой высоте h
кинетическая энергия тела будет равна его потенциальной энергии.
Решение.
В качестве нулевого уровня выберем уровень связанный с начальным положением тела. Потенциальная энергия тела в момент бросания равна нулю, кинетическая энергия равна mv2/2.
Запишем закон сохранения механической энергии (сопротивление среды отсутствует):
mv2/2 = Eк + Ep = Ep + Ep = 2Ep.
Тогда
mv2/2 = 2mgh
Отсюда
h= v2/(4g)
После вычисления
h = 202/(4 × 10) = 10 (м).
Ответ: на высоте 10 м.