- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема Гаусса (закон Гаусса)
Содержание
- 2. Суммарный электрический поток через произвольную замкнутую поверхностьЗакон Гаусса
- 3. Фoрмальное доказательство закона ГауссаТoчечный заряд внутри замкнутой поверхности произвольной формы
- 4. Применение закона Гаусса – альтернативная процедура расчета
- 5. Применение закона Гаусса для различных распределений зарядаЭлектрическое
- 6. Сферическая симметрия – сферическая поверхность Гаусса радиуса
- 7. r < a:Применение закона Гаусса для различных
- 8. Применение закона Гаусса для различных распределений зарядаНепроводящий
- 9. Напряженность электрического поля, создаваемого тонким сферическим слоем(радиус
- 10. Внутри слояr < aПрименение закона Гаусса для
- 11. Применение закона Гаусса для различных распределений зарядаСферически
- 12. Электрическое поле, создаваемое положительно заряженным линейным проводником
- 13. Суммарный заряд внутри поверхности Гаусса равен
- 14. Плоскосимметричное распределение зарядаЭлектрическое поле, создаваемое положительно заряженной
- 15. Электрический потенциал
- 16. Разность потенциалов и электрический потенциалA BВеличина
- 17. Электрический потенциал V = U/q0 в любой
- 18. Силовые линии электрического поля всегда направлены в направлении уменьшения электрического потенциала.Разность потенциалов в однородном электрическом поле
- 19. A BСистема “положительный заряд – электрическое
- 20. Более общий случай:Эквипотенциальная поверхность - произвольная поверхность,
- 21. Электрический потенциал точечных зарядов
- 22. Электрический потенциал точечных зарядов
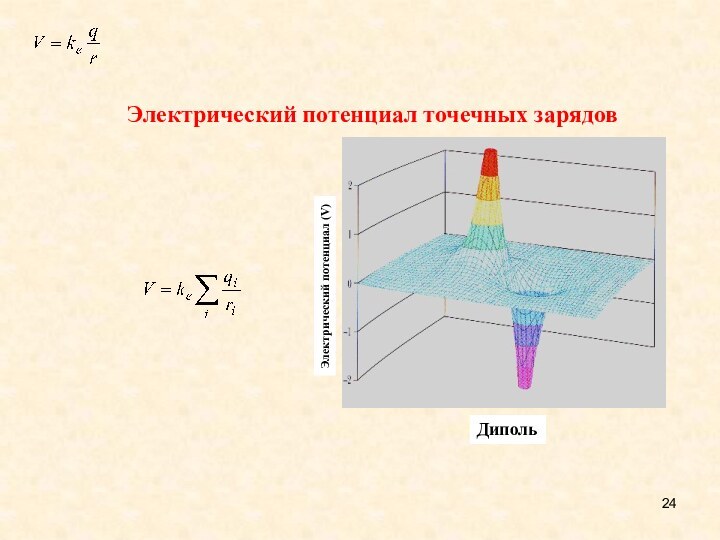
- 23. A single positive chargeЭлектрический потенциал точечных зарядовЭлектрический потенциал (V)Изолированный положительный заряд
- 24. Электрический потенциал точечных зарядовA dipoleЭлектрический потенциал (V)Диполь
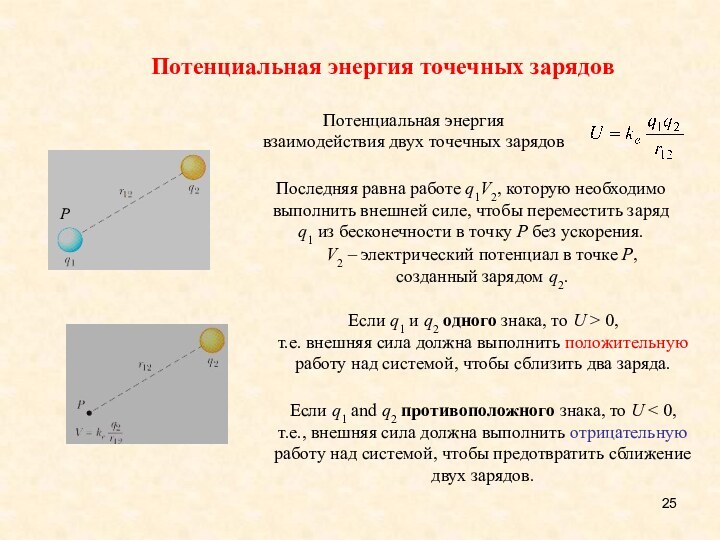
- 25. Потенциальная энергия точечных зарядовV2 – электрический потенциал
- 26. Потенциальная энергия трех точечных зарядовПотенциальная энергия точечных зарядов
- 27. Электрическое поле и электрический потенциалРазность потенциаловЭлектрическое поле - мера скорости изменения электрического потенциала в пространстве.
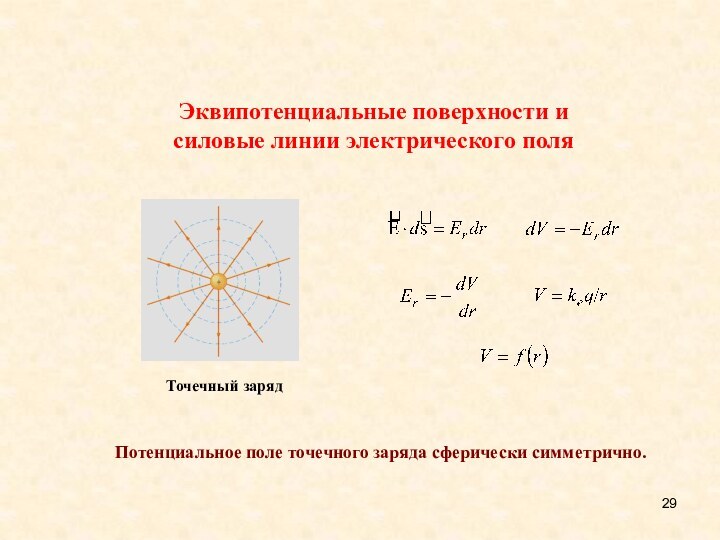
- 28. Эквипотенциальные поверхности и силовые линии электрического поляЭквипотенциальные
- 29. Потенциальное поле точечного заряда сферически симметрично.Эквипотенциальные поверхности и силовые линии электрического поля
- 30. Эквипотенциальные поверхности и силовые линии электрического поля
- 31. Общий случайЭквипотенциальные поверхности и силовые линии электрического поля
- 32. Электрический потенциал диполяТочка P:Точка ( x >>
- 33. Расчет электрического потенциалаПринцип суперпозиции:
- 34. Электрический потенциалнепрерывного распределения зарядов
- 35. Электрический потенциал описывает электростатические явления в более
- 36. Скачать презентацию
- 37. Похожие презентации

























Слайд 3
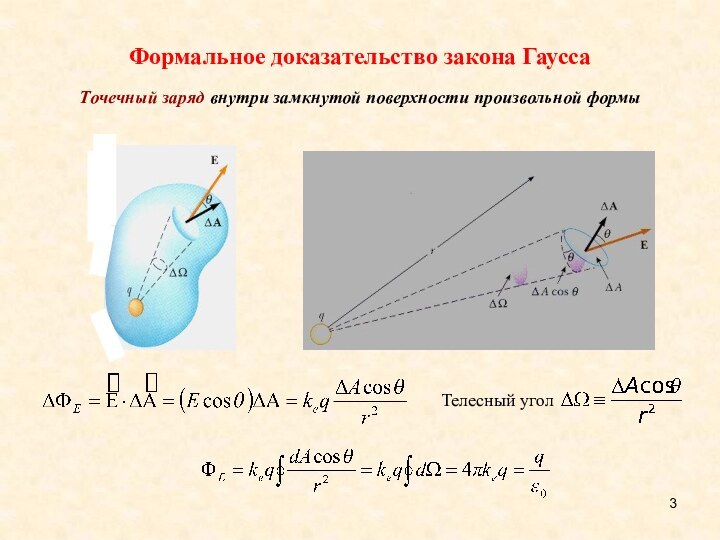
Фoрмальное доказательство закона Гаусса
Тoчечный заряд внутри замкнутой поверхности
произвольной формы
Слайд 4 Применение закона Гаусса – альтернативная процедура расчета электрических
полей.
Закон Гаусса - фундаментальная электростатическая сила,
действующая между точечными
зарядами, обратно пропорциональна квадрату расстояния между ними.
Закон Гаусса удобен для расчета электрических полей
высокосимметричных распределений зарядов.
Применение закона Гаусса
для различных распределений заряда
Слайд 5
Применение закона Гаусса
для различных распределений заряда
Электрическое поле
изолированного точечного заряда
Сферическая симметрия пространства вокруг точечного заряда –
сферическая поверхность Гаусса.Полученный результат эквивалентен результату,
полученному с помощью закона Кулона.
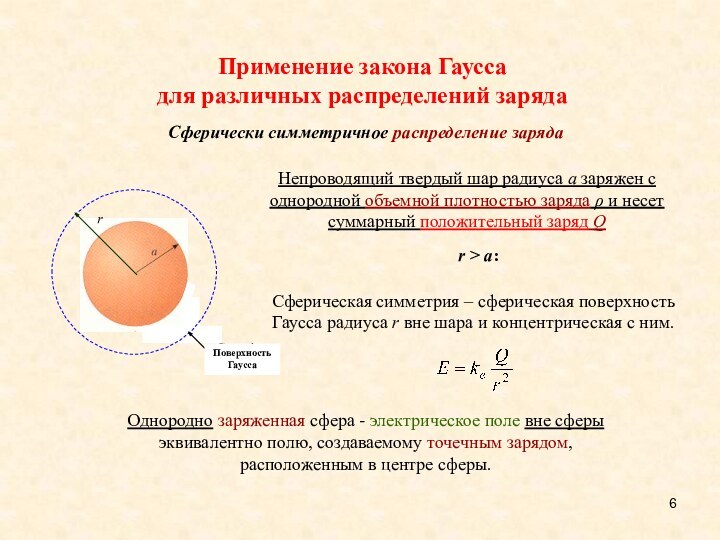
Слайд 6 Сферическая симметрия – сферическая поверхность Гаусса радиуса r
вне шара и концентрическая с ним.
Однородно заряженная сфера -
электрическое поле вне сферы эквивалентно полю, создаваемому точечным зарядом, расположенным в центре сферы.
Непроводящий твердый шар радиуса a заряжен с однородной объемной плотностью заряда и несет суммарный положительный заряд Q
r > a:
Применение закона Гаусса
для различных распределений заряда
Сферически симметричное распределение заряда
Слайд 7
r < a:
Применение закона Гаусса
для различных распределений
заряда
Непроводящий твердый шар радиуса a заряжен с однородной объемной
плотностью заряда и несет суммарный положительный заряд QСферическая симметрия – сферическая поверхность Гаусса радиуса r внутри шара и концентрическая с ним.
Сферически симметричное распределение заряда
Слайд 8
Применение закона Гаусса
для различных распределений заряда
Непроводящий твердый
шар радиуса a заряжен с однородной объемной плотностью заряда
и несет суммарный положительный заряд QСферически симметричное распределение заряда
Слайд 9
Напряженность электрического поля, создаваемого тонким сферическим слоем
(радиус a,
общий заряд Q однородно распределен по поверхности слоя)
Вне
слояr > a
Напряженность электрического поля вне слоя аналогична той, что создается точечным зарядом Q, расположенным в центре шара, которому принадлежит слой.
Применение закона Гаусса
для различных распределений заряда
Сферически симметричное распределение заряда
Слайд 10
Внутри слоя
r < a
Применение закона Гаусса
для различных
распределений заряда
Сферически симметричное распределение заряда
Напряженность электрического поля, создаваемого тонким
сферическим слоем(радиус a, общий заряд Q однородно распределен по поверхности слоя)
Слайд 11
Применение закона Гаусса
для различных распределений заряда
Сферически симметричное
распределение заряда
Напряженность электрического поля, создаваемого тонким сферическим слоем
(радиус a,
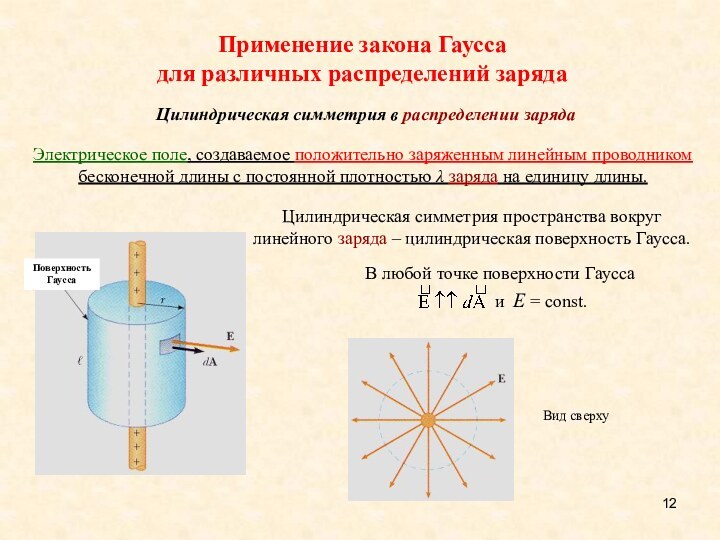
общий заряд Q однородно распределен по поверхности слоя) Слайд 12 Электрическое поле, создаваемое положительно заряженным линейным проводником бесконечной
длины с постоянной плотностью заряда на единицу длины.
Цилиндрическая
симметрия пространства вокруг линейного заряда – цилиндрическая поверхность Гаусса.Применение закона Гаусса
для различных распределений заряда
Цилиндрическая симметрия в распределении заряда
Слайд 13 Суммарный заряд внутри поверхности Гаусса равен l.
Применение закона Гаусса
для различных распределений заряда
Цилиндрическая симметрия в
распределении зарядаЭлектрическое поле, создаваемое положительно заряженным линейным проводником бесконечной длины с постоянной плотностью заряда на единицу длины.
Слайд 14
Плоскосимметричное распределение заряда
Электрическое поле, создаваемое положительно заряженной плоскостью
с однородной поверхностной плотностью заряда
Плоская симметрия пространства вокруг
линейного заряда – поверхность Гаусса - маленький цилиндр.
Боковая поверхность цилиндра не пересекается силовыми линиями электрического поля.
Общий заряд внутри поверхности Гаусса равен qвнутри = A.
E - const
Применение закона Гаусса
для различных распределений заряда
Слайд 16
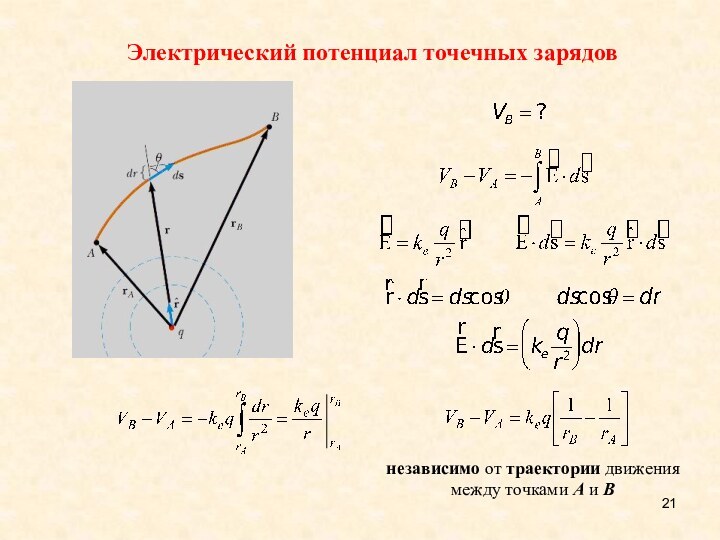
Разность потенциалов и электрический потенциал
A B
Величина этого
линейного интеграла не зависит от траектории перемещения
заряда из
точки A в точку B, поскольку электрическая сила консервативна. Слайд 17 Электрический потенциал V = U/q0 в любой точке
электрического поля
не зависит от величины q0.
1 эВ =
1.60 × 10-19 Кл В = 1.60 × 10-19 ДжРазность потенциалов и электрический потенциал
Слайд 18 Силовые линии электрического поля всегда направлены в направлении
уменьшения электрического потенциала.
Разность потенциалов в однородном электрическом поле
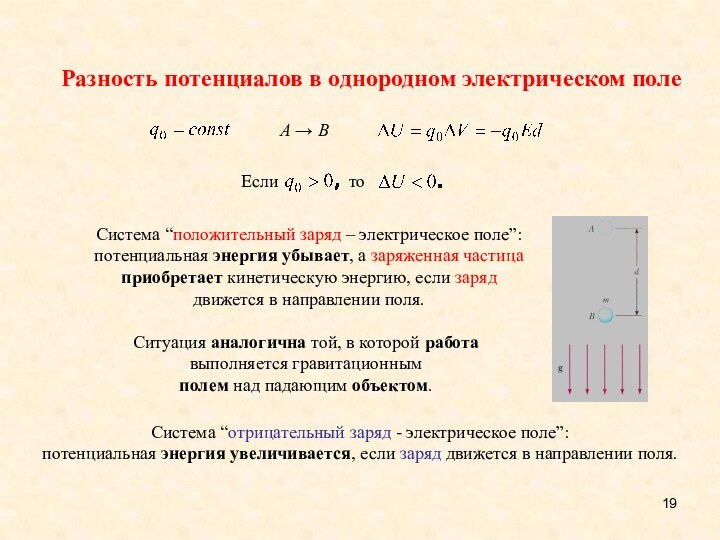
Слайд 19
A B
Система “положительный заряд – электрическое поле”:
потенциальная
энергия убывает, а заряженная частица приобретает кинетическую энергию, если
заряд движется в направлении поля.Система “отрицательный заряд - электрическое поле”:
потенциальная энергия увеличивается, если заряд движется в направлении поля.
Разность потенциалов в однородном электрическом поле
Слайд 20
Более общий случай:
Эквипотенциальная поверхность - произвольная поверхность, состоящая
из непрерывного распределения точек с одним и тем же
электрическим потенциалом.Разность потенциалов в однородном электрическом поле
Слайд 23
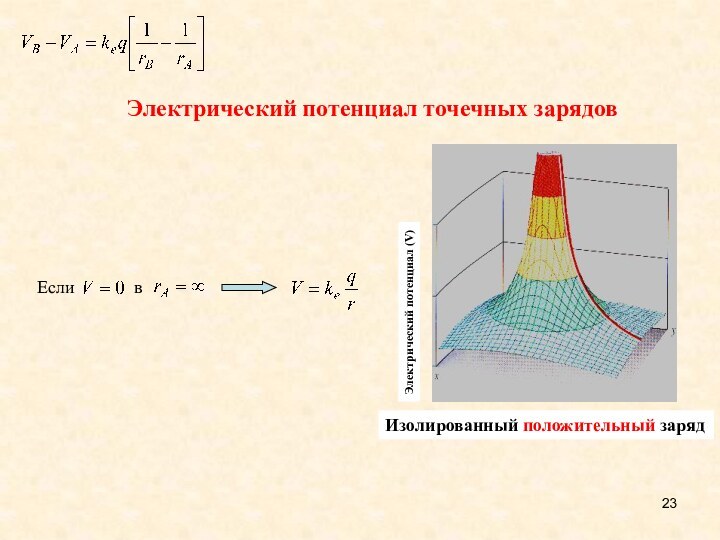
A single positive charge
Электрический потенциал точечных зарядов
Электрический потенциал
(V)
Изолированный положительный заряд
Слайд 25
Потенциальная энергия точечных зарядов
V2 – электрический потенциал в
точке P,
созданный зарядом q2.
Последняя равна работе q1V2,
которую необходимо выполнить внешней силе, чтобы переместить заряд q1 из бесконечности в точку P без ускорения. Если q1 и q2 одного знака, то U > 0,
т.е. внешняя сила должна выполнить положительную работу над системой, чтобы сблизить два заряда.
Если q1 and q2 противоположного знака, то U < 0,
т.е., внешняя сила должна выполнить отрицательную работу над системой, чтобы предотвратить сближение двух зарядов.
P
Слайд 27
Электрическое поле и электрический потенциал
Разность потенциалов
Электрическое поле -
мера скорости изменения электрического потенциала в пространстве.
Слайд 28
Эквипотенциальные поверхности и
силовые линии электрического поля
Эквипотенциальные поверхности
всегда должны быть перпендикулярны силовым линиям электрического поля и
пересекать их.
Слайд 29
Потенциальное поле точечного заряда сферически симметрично.
Эквипотенциальные поверхности и
силовые линии электрического поля
Слайд 32
Электрический потенциал диполя
Точка P:
Точка ( x >> a
):
Точка (P между зарядами):
Точка (P расположена слева от отрицательного
заряда):
Слайд 33
Расчет электрического потенциала
Принцип суперпозиции:
Электрический потенциал, создаваемый в произвольной точке P непрерывным распределением
зарядов, равен интегралу потенциалов точечных зарядов, соответствующих этому распределению.II. Расчет линейного интеграла от
V обычно предполагается равным 0 в точке, расположенной бесконечно далеко от зарядов.
Электрический потенциал системы точечных зарядов равен алгебраической (скалярной) сумме потенциалов точечных зарядов.
для заданного распределения зарядов.
Слайд 35 Электрический потенциал описывает электростатические явления в более упрощенной
форме, чем это можно сделать используя понятия об электростатическом
поле и электрических силах.Электрический потенциал