Презентация на тему Тепловое излучение

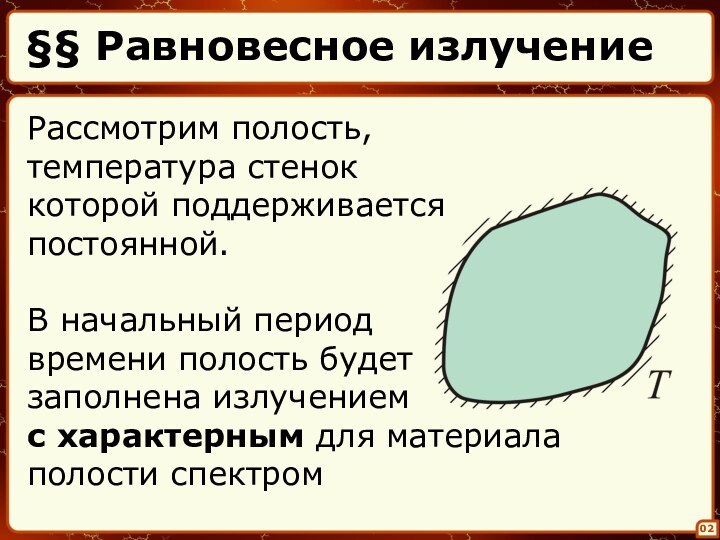
постоянной.
В начальный период
времени полость будет
заполнена излучением
с характерным

атомы полости переходят в возбужденное состояние и излучают.
При этом

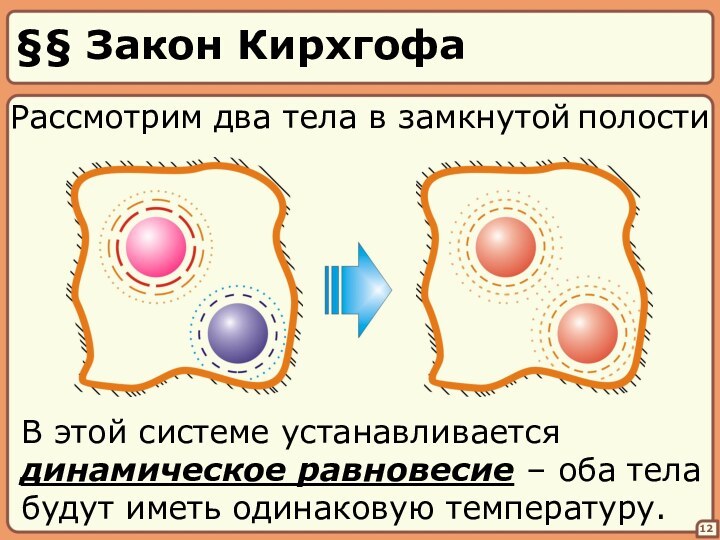
Система постепенно переходит в
состояние равновесия, которому
соответствует наибольшая вероятность.

Это излучение называется равновесным.

характе-
ристики не зависят от свойств материала
стенок полости (и тел

Излучение также можно характеризовать
этой температурой и считать ее свойством
самого излучения, которое также
называется тепловым.

Только тепловое излучение может быть
равновесным.

поглощает больше,
чем излучает (т.е. нагревается),
либо излучает, за счет убыли

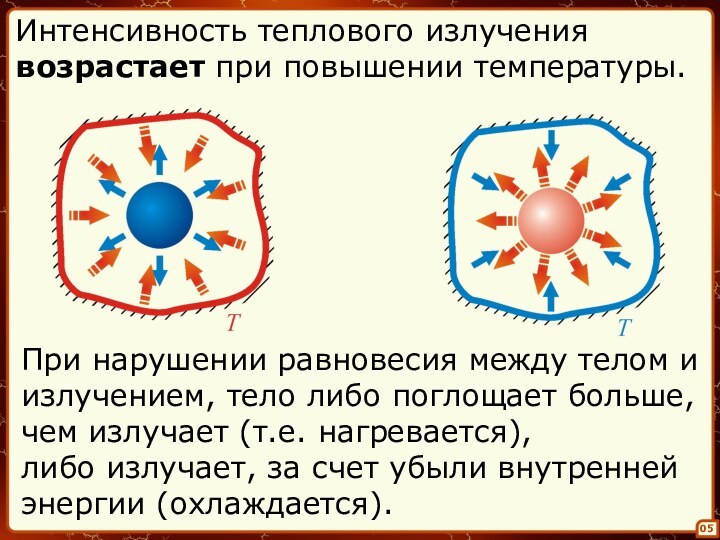
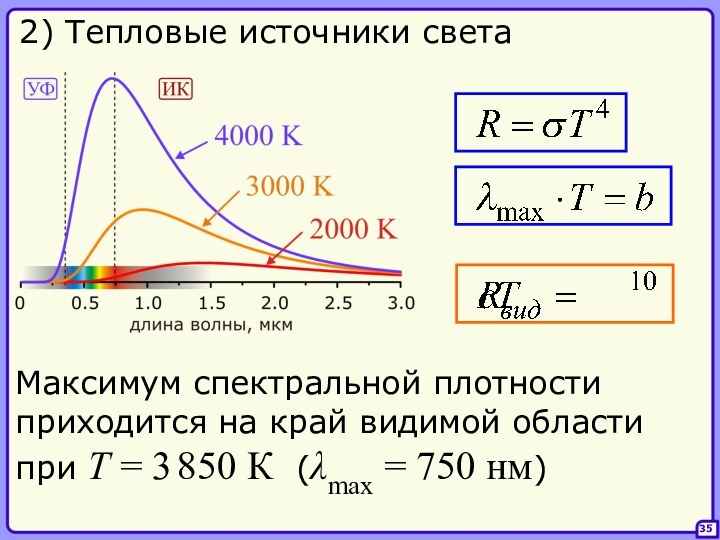
Интенсивность теплового излучения
возрастает при повышении температуры.

волнами,
за единицу времени со всей
площади тела

Это, например, та мощность,

07

Энергетической светимостью

называется величина, равная
мощности теплового излучения

с единицы площади тела.

[R] = 1 Вт/м2

Эти величины – интегральные,

т.е. учитывают энергию, переносимую
волнами всех частот (длин волн)

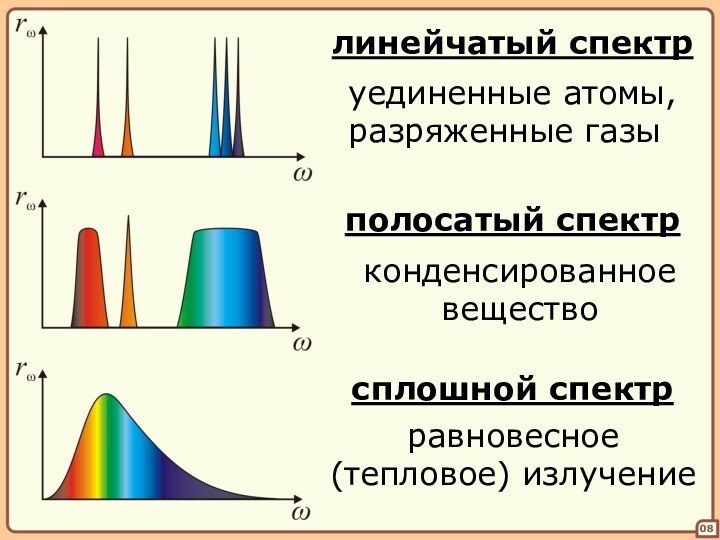
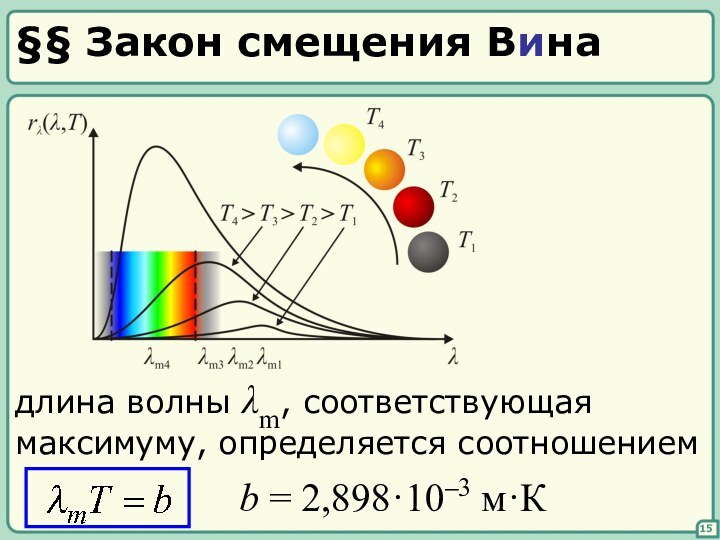
Рассмотрим спектры

светимости
Это энергия, излучаемая телом в единицу времени с единицы

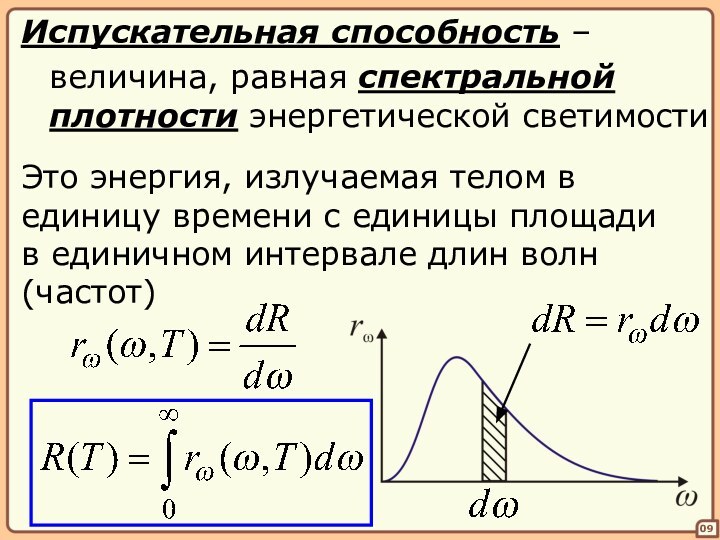
в единичном интервале длин волн (частот)

[ω, ω + dω]
Пусть
называется
поглощательной
способностью
тогда безразмерная величина

тела,
частоты падающего излучения.
температуры,
состояния поверхности,

Тело называют серым, если

этой системе устанавливается
динамическое равновесие

функция
Кирхгофа
13
Если тело обладает большей излучательной способностью,
то оно

и, для поддержания
температуры, такое тело должно
больше поглощать.

Кирхгоф, 1859

или испускательная
способность абсолютно черного тела.

тела
Больцман, 1884, теоретический расчет

– только для
АЧТ
– постоянная
Стефана–Больцмана

определяется соотношением
b = 2,898·10–3 м·К

(1905), вывод выражения для спектральной плотности излучения в полости.
Полная

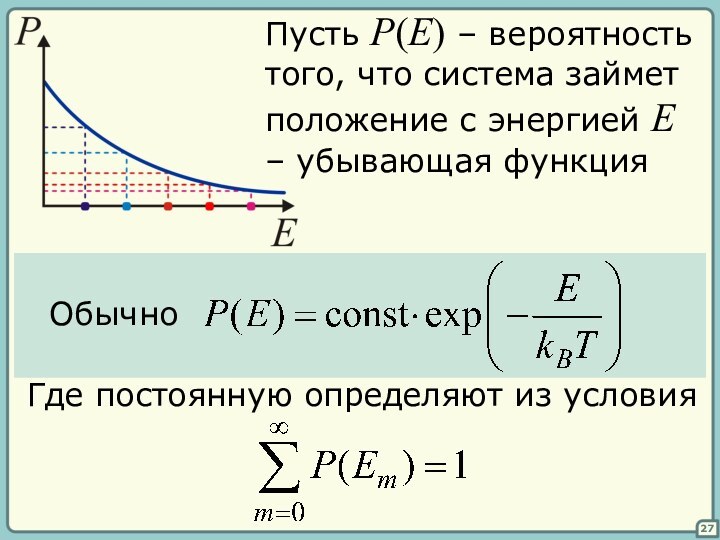
объемная плотность энергии ЭМВ

– энергия, приходящаяся на

17

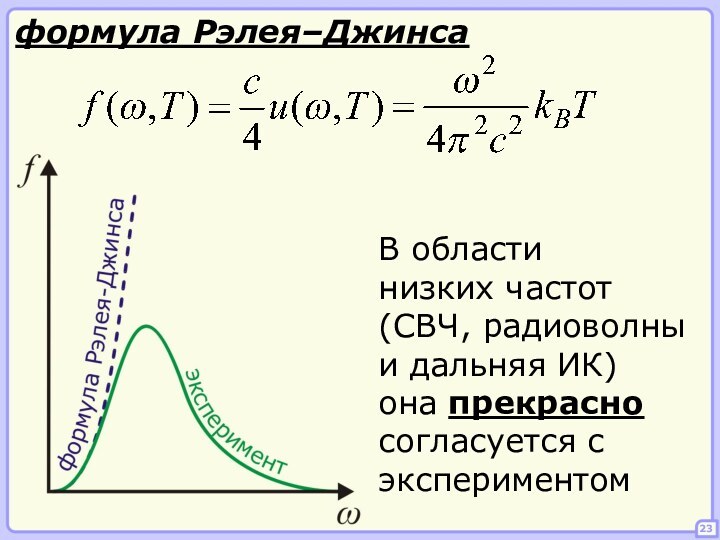
Энергия ЭМВ распределена по частотам неравномерно

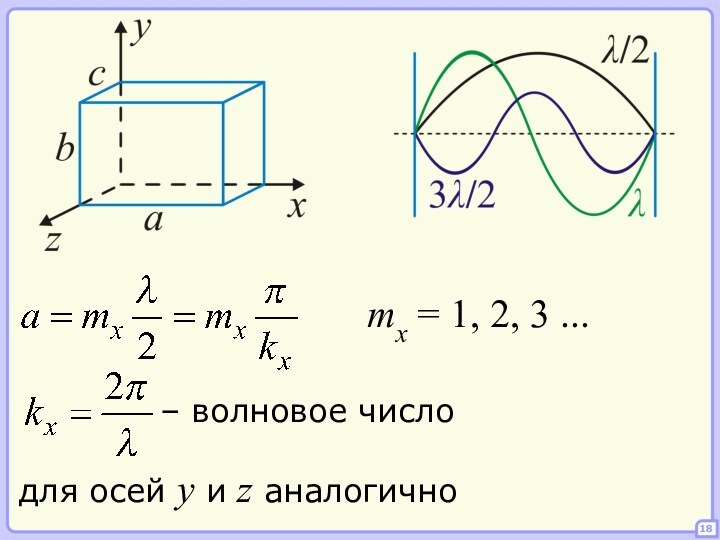
Предположим, что равновесное излучение в полости

представляет собой
систему стоячих волн.

а форма полости – параллелепипед
со сторонами a, b и c.

Пусть поверхность стенок – зеркальная,

и z аналогично

от k.
– объем, занимаемый
всеми состояниями

– объем одного состояния

dω] равно
Учтем независимость двух состояний
поляризации (умножим на 2):

закона Больцмана следует, что на
каждую степень свободы приходится
одинаковая энергия

а на колебательную степень свободы –
энергия kBT.

дальняя ИК)
она прекрасно
согласуется с
экспериментом

телом и излучением
2) уменьшение спектральной
плотности для

на одно колебание)
25

набор осцилляторов,
которые могут занимать лишь
дискретный ряд уровней.
–

– E1 – возбужденное состояние

– Em – m-й уровень

с энергией E
– убывающая функция
Обычно
Где постоянную определяют из

и
определяется только свойствами излучения
Пусть энергия поглощается/излучается
квантами (порциями) с

закон Стефана–Больцмана
2) закон смещения Вина
3) описание спектра теплового

АЧТ с T ≈ 6000 K (λm ≈ 0.47μ)

край видимой области
при T = 3 850 К (λmax

19 в. изобрел
дуговую лампу
Лодыгин, 1872
T

Гейсер в 1856 г. изобрел флуоресцентную лампу

лампы
Пары ртути в инертном газе
(аргон, неон) испускают
ультрафиолет,

Такие лампы потребляют в 5 раз меньше
энергии. Срок службы достигает 15000 ч.

(азот)
при Tк: P~0.5 атм.
Лампа накаливания

большей
светоотдаче.
срок службы: 500-1500 ч.
КПД не превышает 5%
(у лучших источников

Галогеновые лампы имеют
кварцевую колбу, а внутри –
инертный газ с добавками
галогенов

, чтобы испаряющийся
вольфрам вновь осаждался на спирали

40

«Ксеноновые» лампы

англ.: HID
(High Intensity Discharge)

источником света является
электрическая дуга в газоразрядной
камере с инертными газами

мощность: 75 Вт - 50 кВт

Для их розжига нужен мощный разряд
— порядка 25 киловольт.

освещение
(при T ~ 6700 K ηmax ~ 14%
с