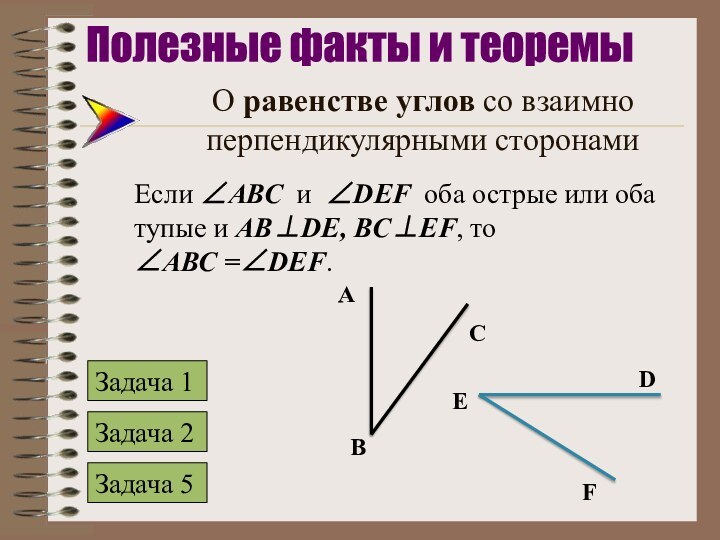
и DEF оба острые или оба тупые и АВDE,
BCEF, тоАВС =DEF.
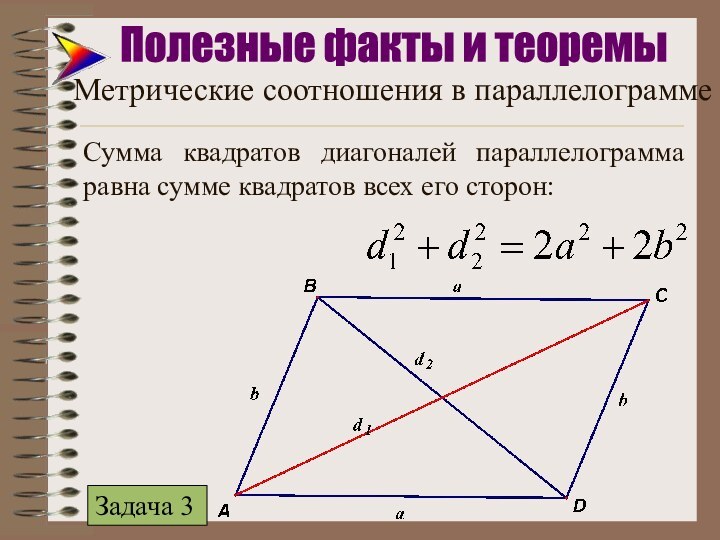
Полезные факты и теоремы
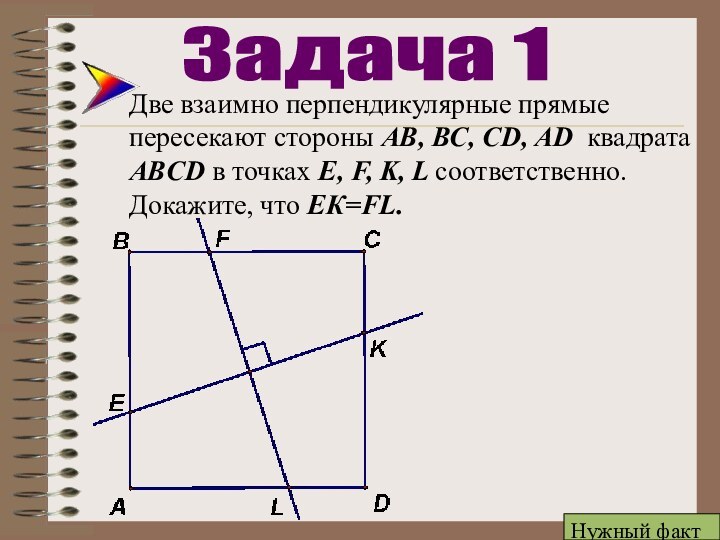
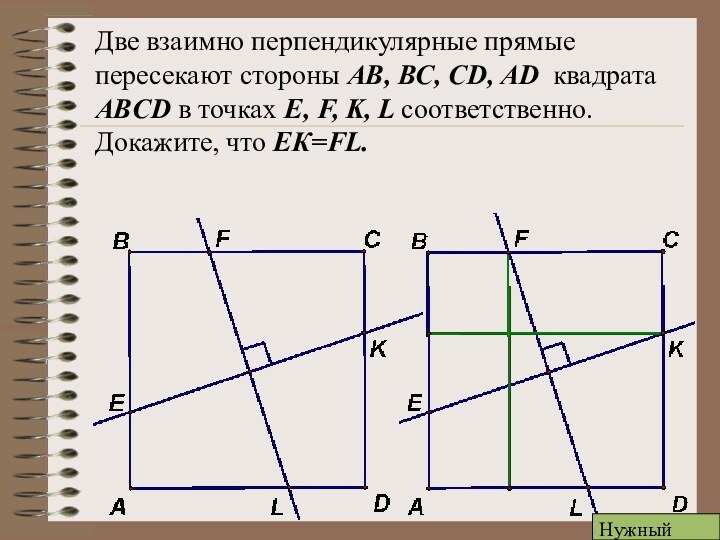
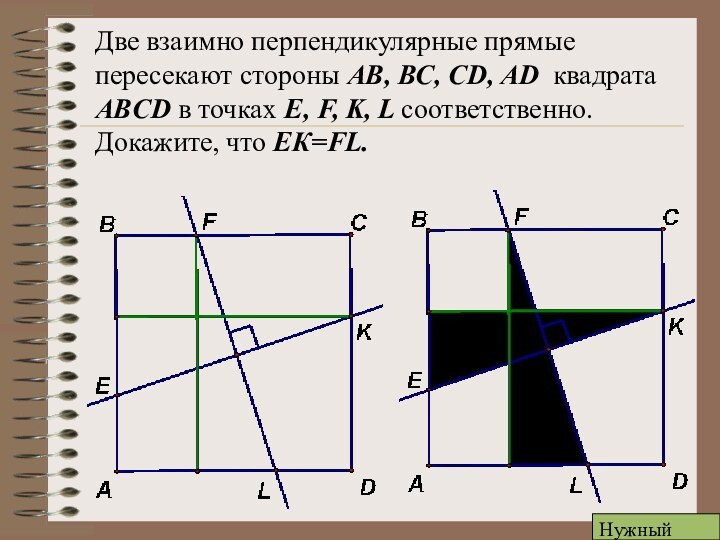
Задача 1
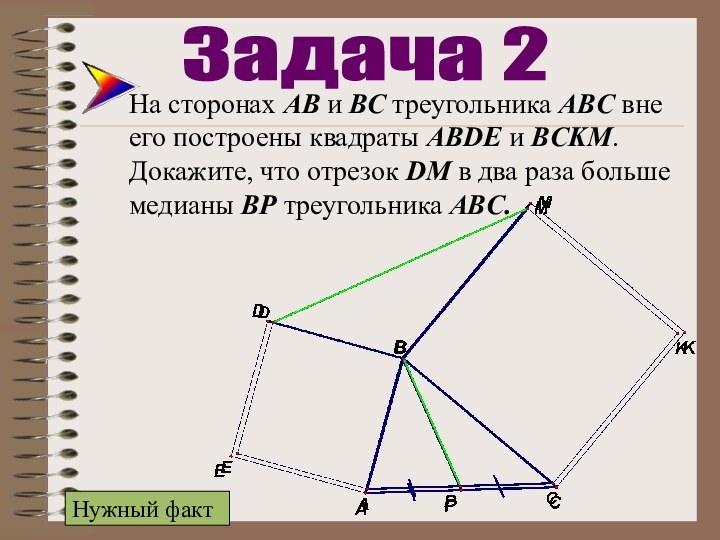
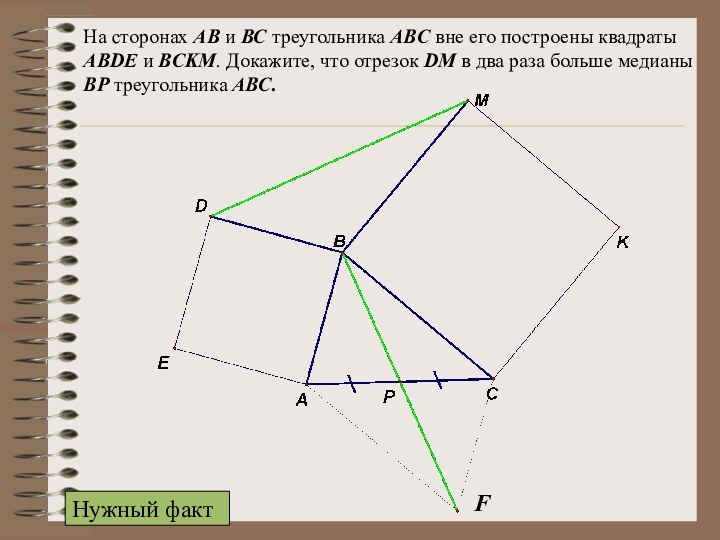
Задача 2
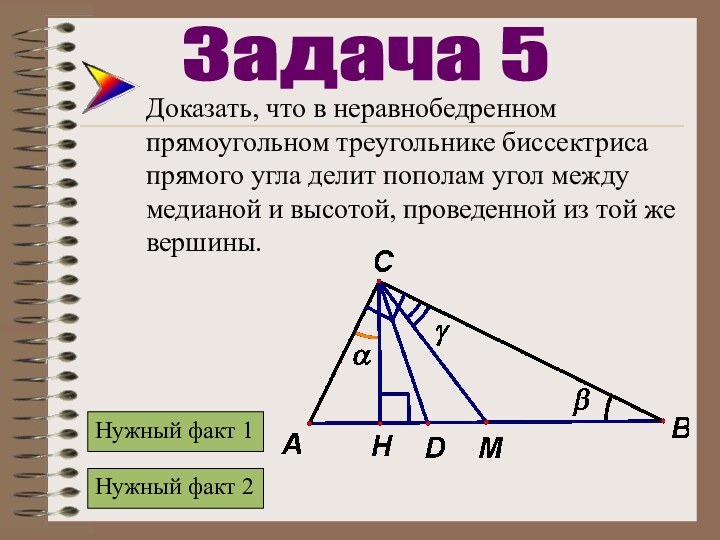
Задача 5
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть











Полезные факты и теоремы
Задача 1
Задача 2
Задача 5
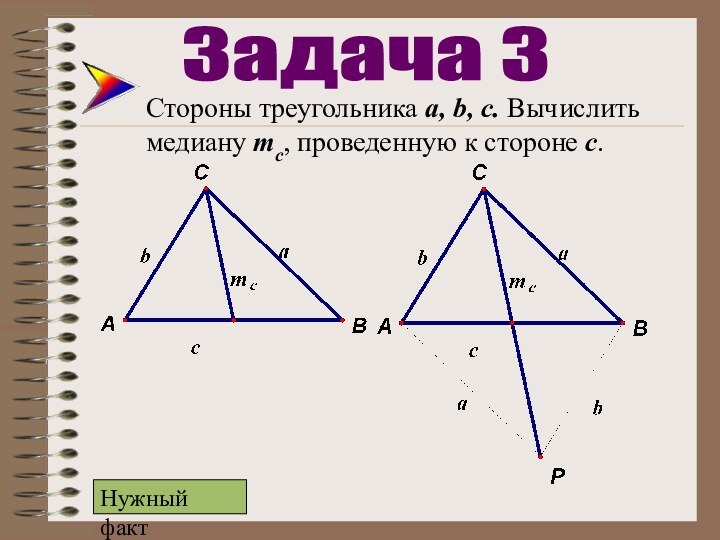
Три медианы треугольника пересекаются в одной точке (центроид треугольника) и делятся ею в отношении 2:1, считая от вершины.
Полезные факты и теоремы
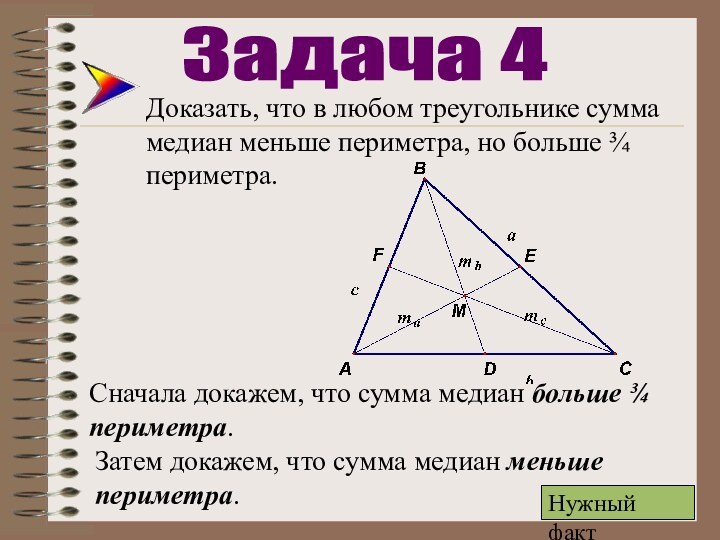
Задача 4
Средняя линия равна полусумме оснований трапеции.
Эти теоремы справедливы и для средней линии треугольника.
Полезные факты и теоремы
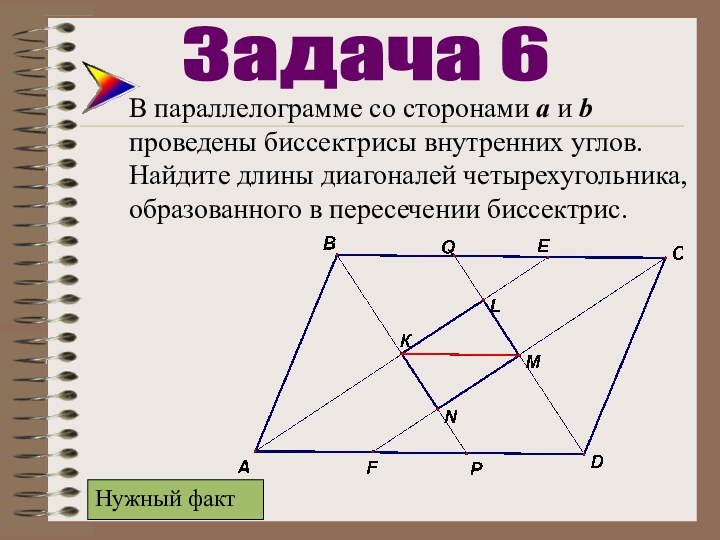
Задача 6
Обратная теорема
Полезные факты и теоремы
Задача 5
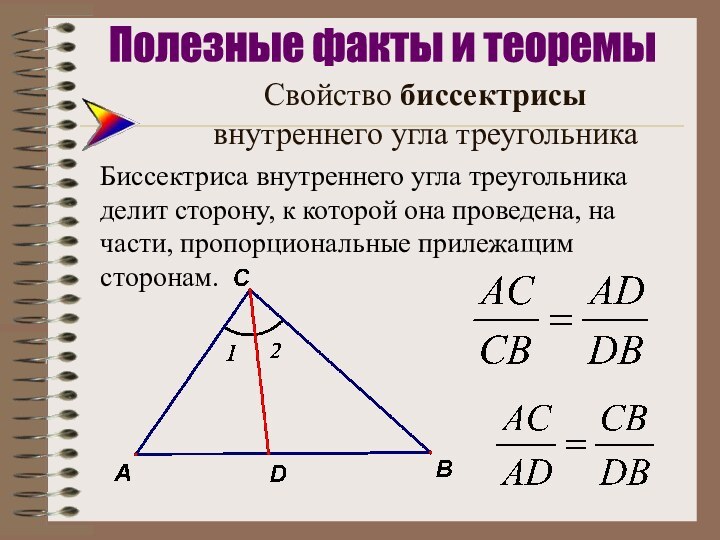
Полезные факты и теоремы
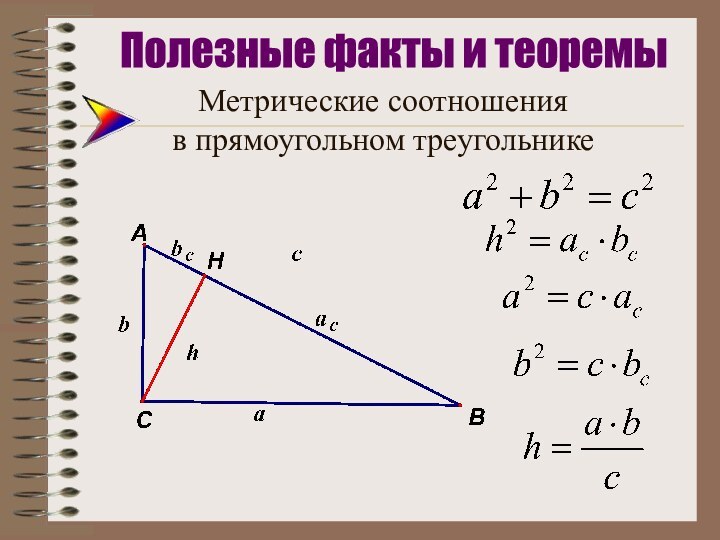
Полезные факты и теоремы
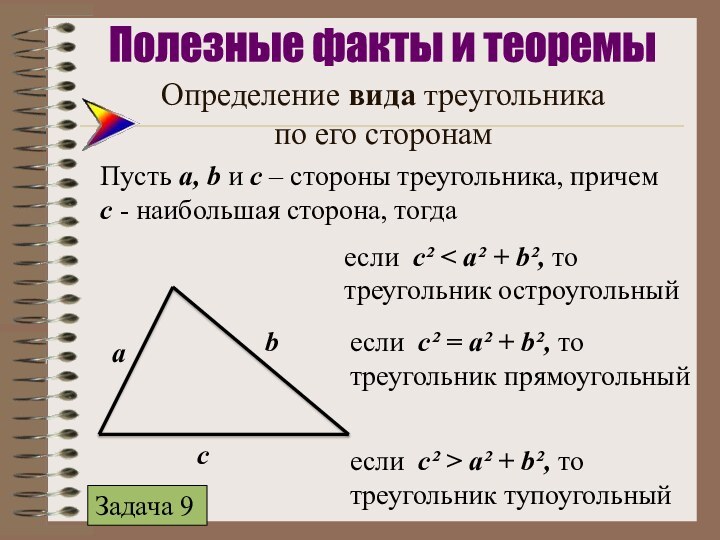
если с² < а² + b², то
треугольник остроугольный
если с² = а² + b², то
треугольник прямоугольный
если с² > а² + b², то
треугольник тупоугольный
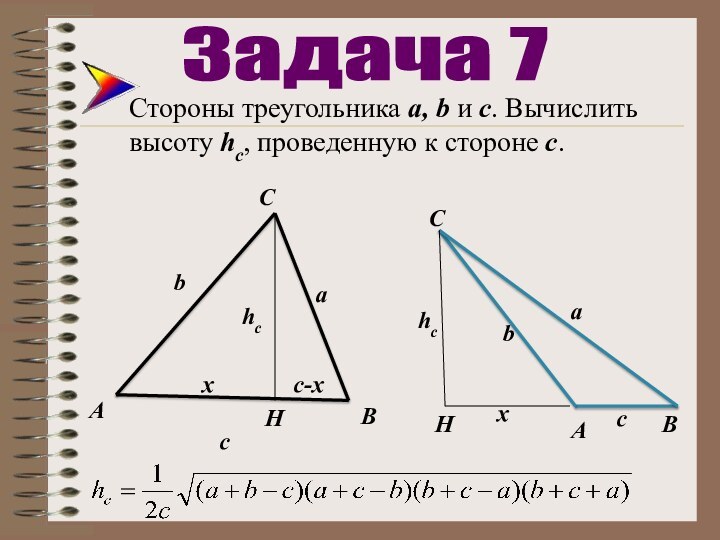
Задача 9
Полезные факты и теоремы
Обобщенная теорема подобия
Соответственные линейные элементы: медианы, высоты, биссектрисы, периметры, радиусы описанной и вписанной окружностей.
Задача 9
Три пути доказательства
равенства отрезков
Рассмотреть эти отрезки как стороны одного треугольника и доказать, что треугольник равнобедренный.
Дополнительные построения, связанные с окружностью.
Задача 1
Нужный факт
Нужный факт
Нужный факт
Задача 2
Нужный факт
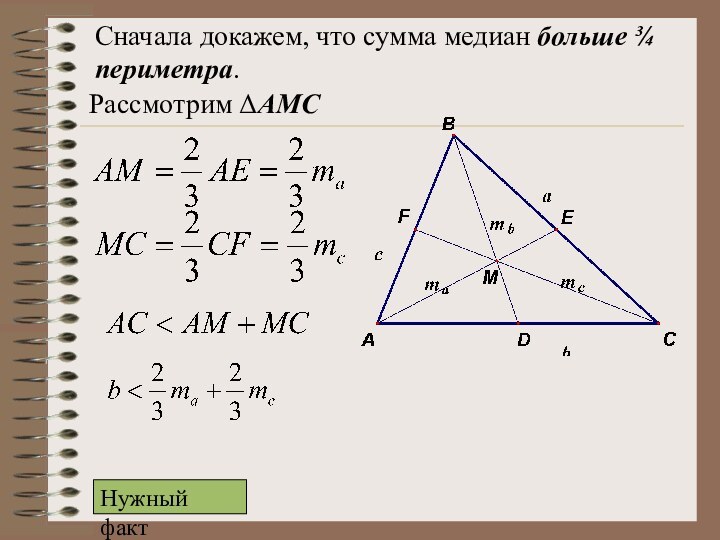
F
Нужный факт
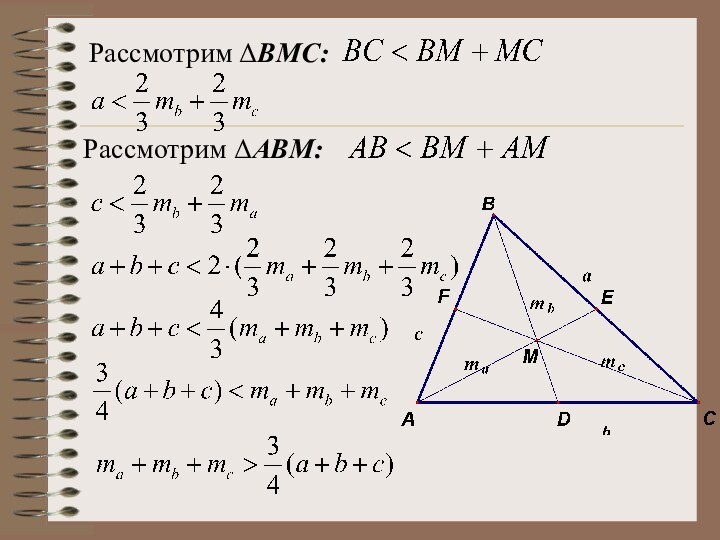
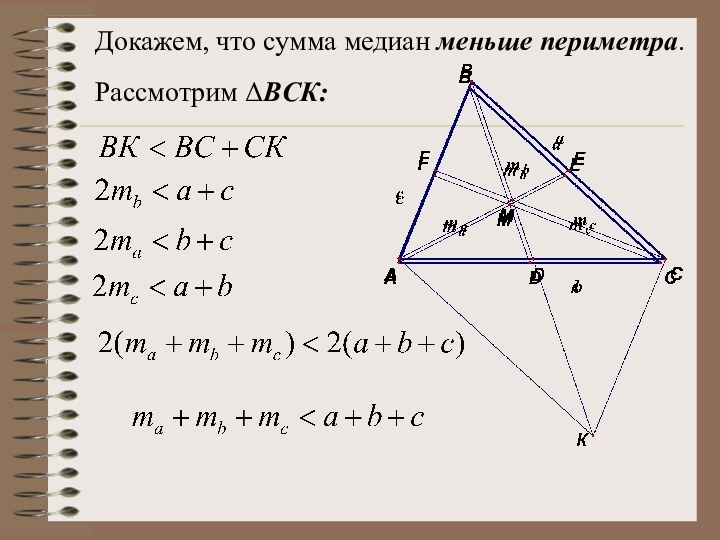
Затем докажем, что сумма медиан меньше периметра.
Нужный факт
Задача 5
Нужный факт 2
Нужный факт 1
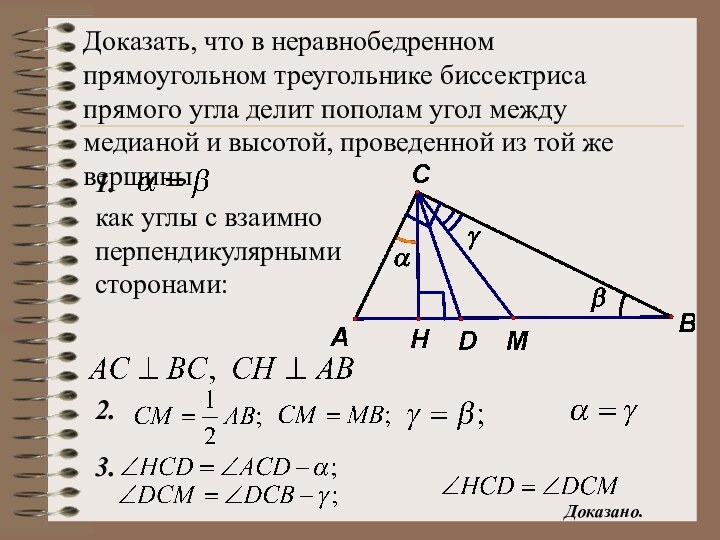
как углы с взаимно перпендикулярными сторонами:
1.
2.
3.
Доказано.
Задача 6
Нужный факт
3.
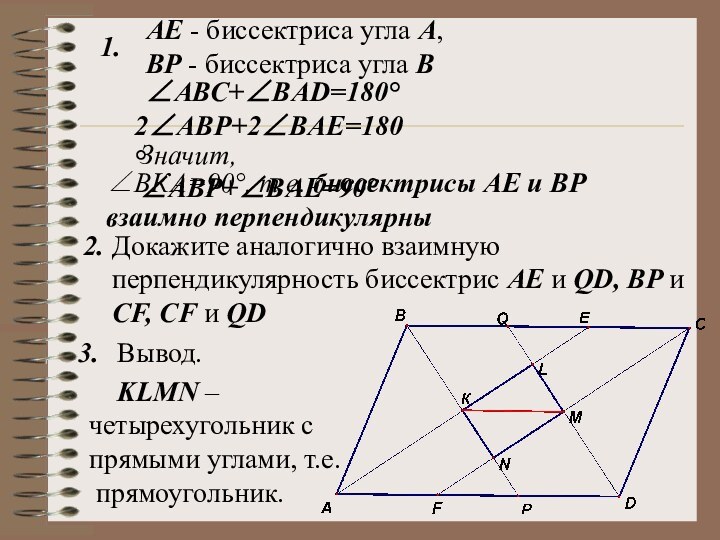
АВС+BAD=180°
2АВP+2BAE=180°
Значит, АВP+BAE=90°
ВКА=90°, т.е. биссектрисы АЕ и ВР
взаимно перпендикулярны
Докажите аналогично взаимную перпендикулярность биссектрис АЕ и QD, BP и CF, CF и QD
Вывод.
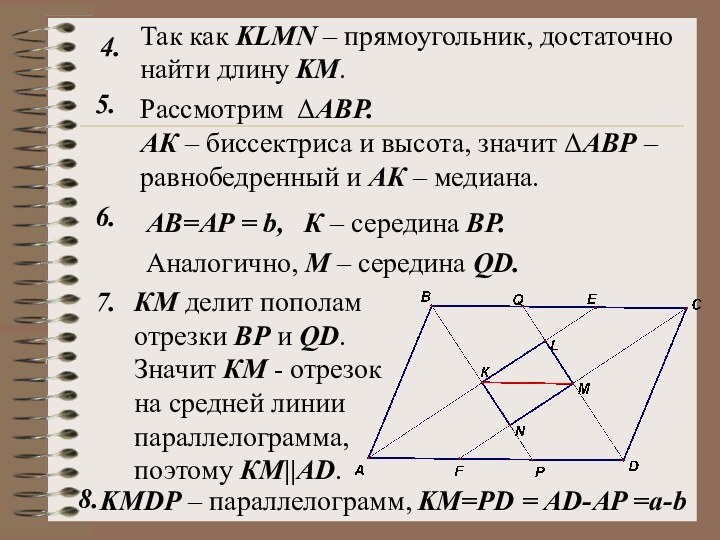
6.
АВ=АP = b,
К – середина ВР.
Аналогично, М – середина QD.
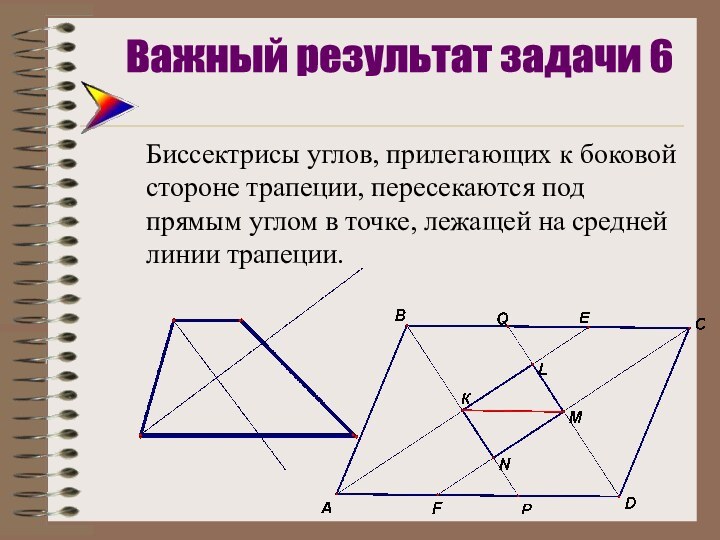
КМ делит пополам отрезки BP и QD. Значит КМ - отрезок на средней линии параллелограмма, поэтому КМAD.
8.
KMDP – параллелограмм,
Важный результат задачи 6
Замечание
В качестве опорного элемента часто выбирается площадь фигуры. Тогда говорят, что используется метод площадей.
Замечание
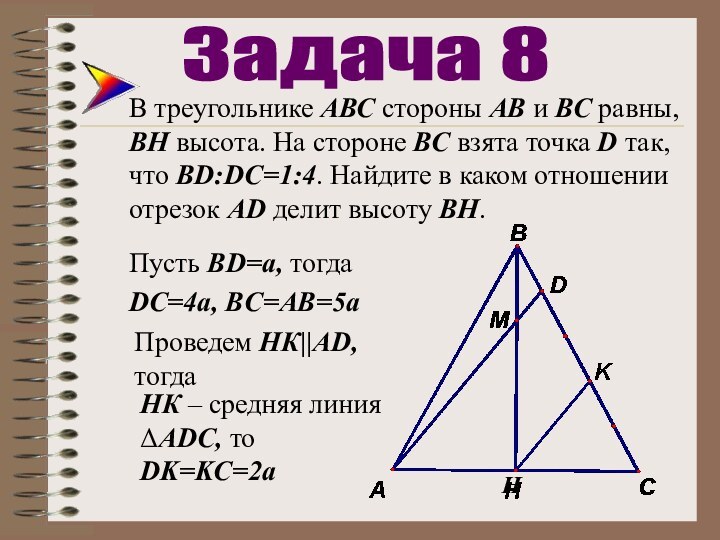
Задача 8
Пусть ВD=a, тогда
DС=4a, BC=AВ=5а
Проведем НКAD, тогда
НК – средняя линия ADС, то DK=KC=2a
H
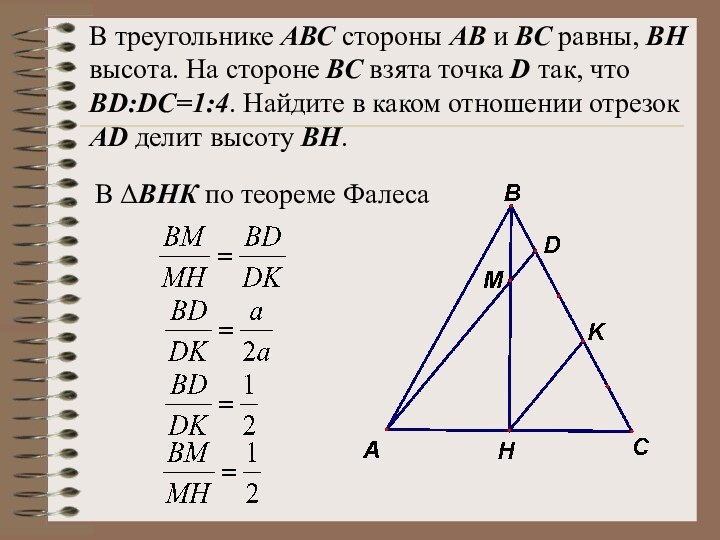
В ВНК по теореме Фалеса
Задача 9
Нужный факт
Определим вид треугольника.
Значит, треугольник тупоугольный.
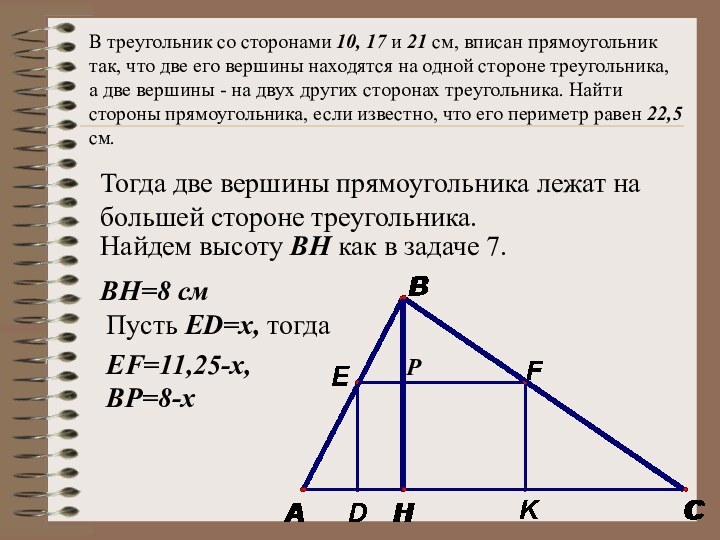
Тогда две вершины прямоугольника лежат на большей стороне треугольника.
Найдем высоту ВН как в задаче 7.
ВН=8 см
Пусть ЕD=х, тогда
EF=11,25-x,
ВР=8-x
P
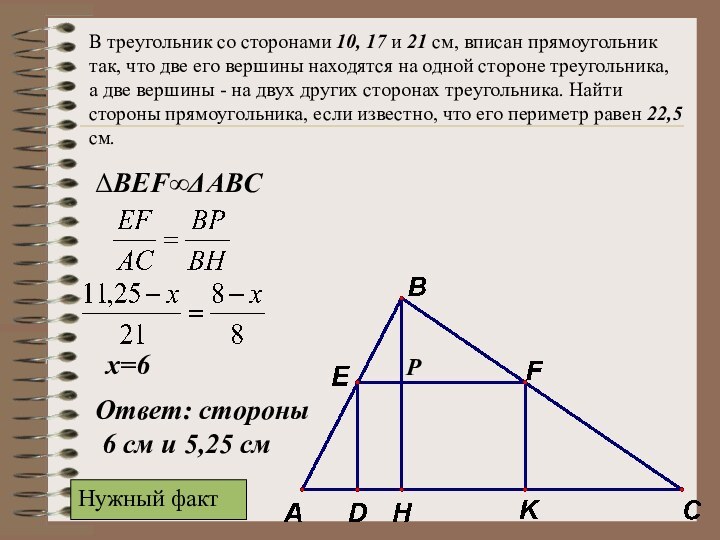
ВEFABC
x=6
P
Нужный факт
Ответ: стороны
6 см и 5,25 см
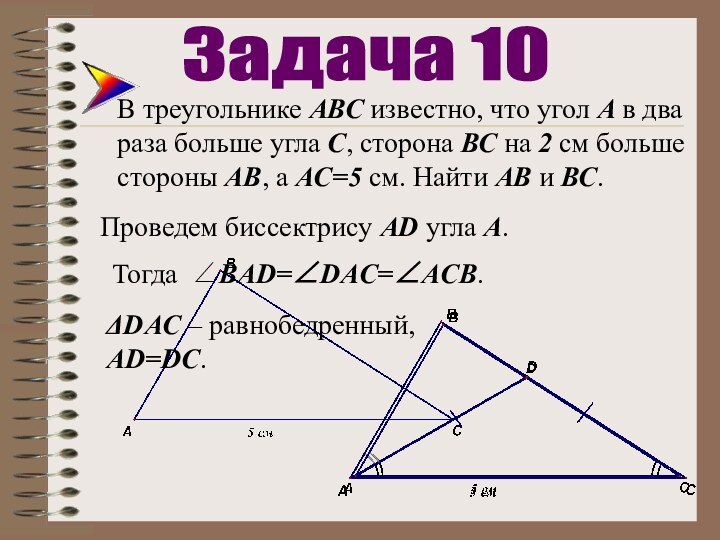
Задача 10
Проведем биссектрису AD угла А.
Тогда ВАD=DAC=АCB.
DAC – равнобедренный,
АD=DC.
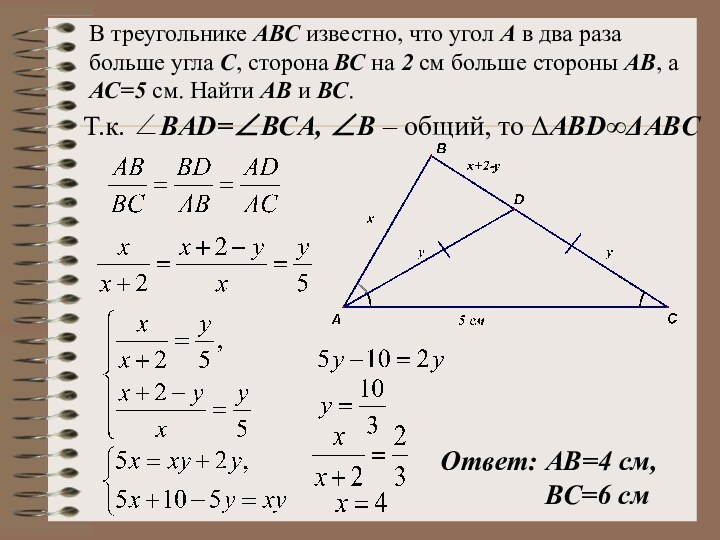
Т.к. ВАD=ВСA, B – общий, то АВDABC
Ответ: АВ=4 см,
ВС=6 см