- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
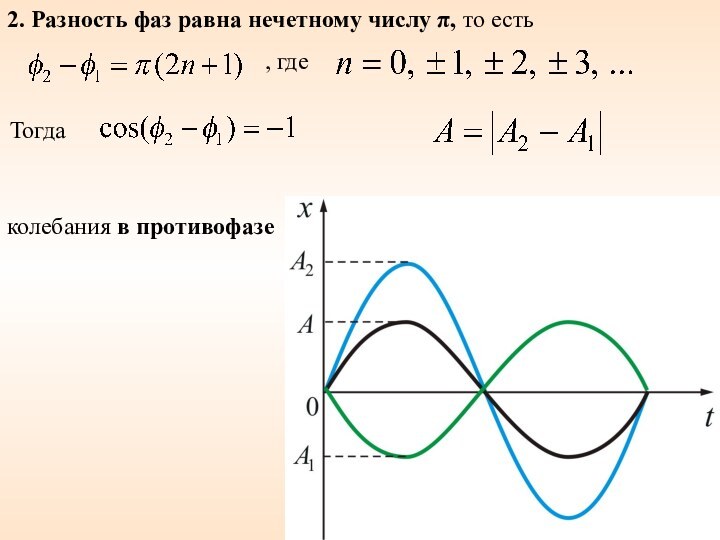
- Экология
- Экономика
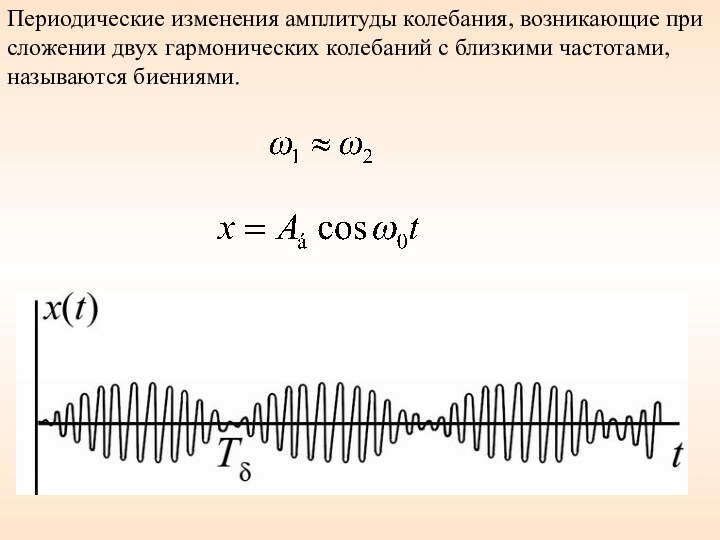
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
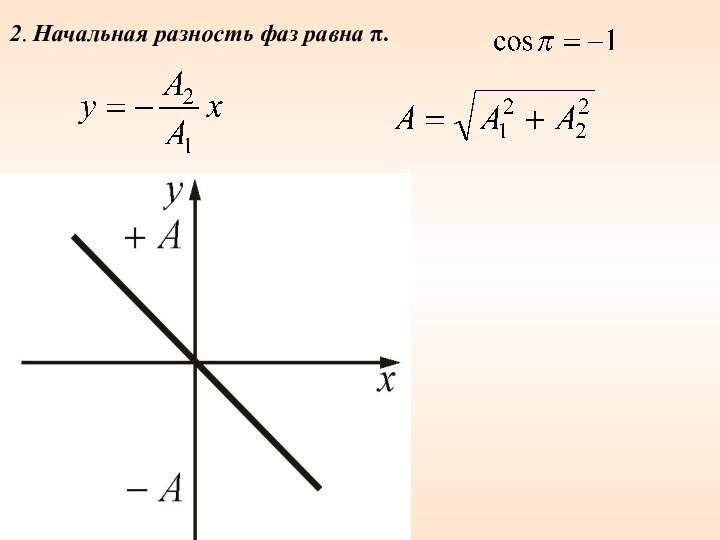
Email: Нажмите что бы посмотреть
Презентация на тему Уравнения колебаний
Содержание
- 2. Примеры колебательных процессов Круговая волна
- 3. Возможные типы колебаний атомов
- 4. 1. Виды и признаки колебанийКолебания делятся на
- 5. Колебательное движение является периодическим.
- 6. x = 0 – положение
- 7. Три признака колебательного движения:повторяемость (периодичность) – движение
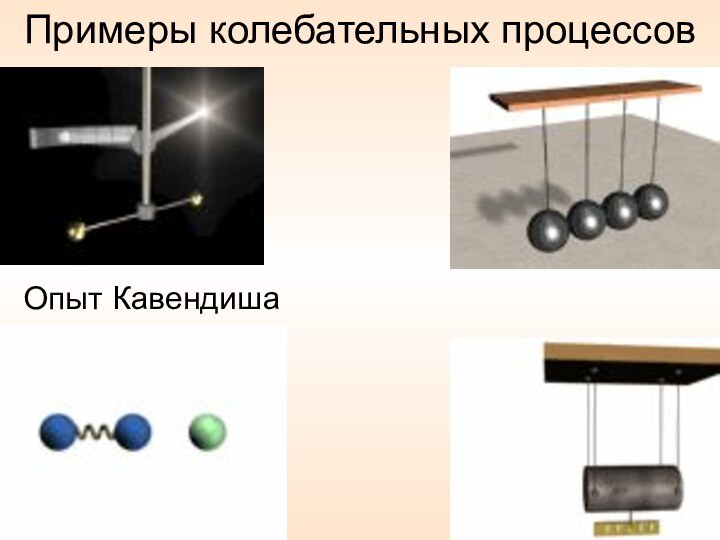
- 8. Примеры колебательных процессовОпыт Кавендиша
- 9. Колебания называются периодическими, если
- 10. Различные периодические процессы (повторяющиеся через равные
- 11. Расстояние груза от положения равновесия до
- 15. Частота колебаний ν определяется, как число полных
- 16. ω – циклическая (круговая) частота
- 17. – амплитуда скорости; – амплитуда ускорения.
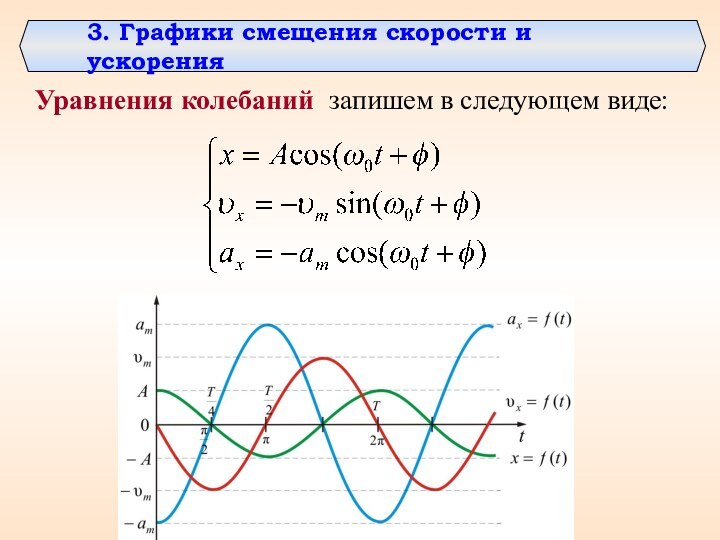
- 18. 3. Графики смещения скорости и ускорения Уравнения колебаний запишем в следующем виде:
- 20. Скорость колебаний тела максимальна и
- 21. Найдем разность фаз φ между фазами смещения
- 22. 4. Основное уравнение динамики гармонических колебаний Исходя
- 23. Получим основное уравнение динамики гармонических колебаний, вызываемых
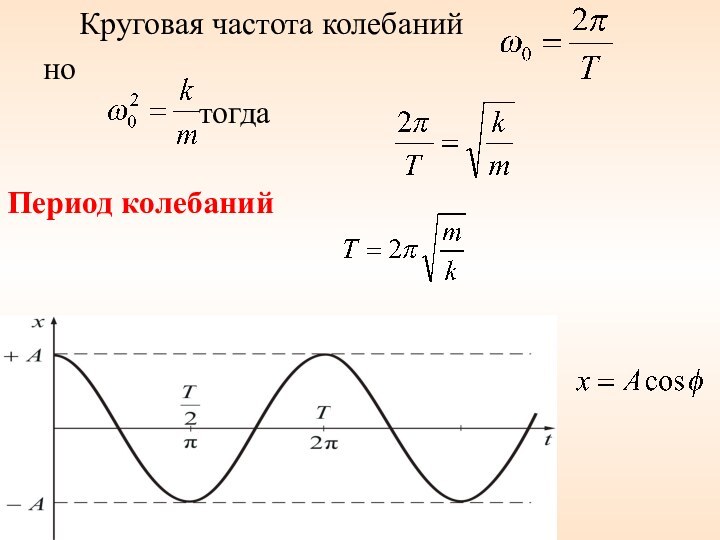
- 24. Круговая частота колебаний
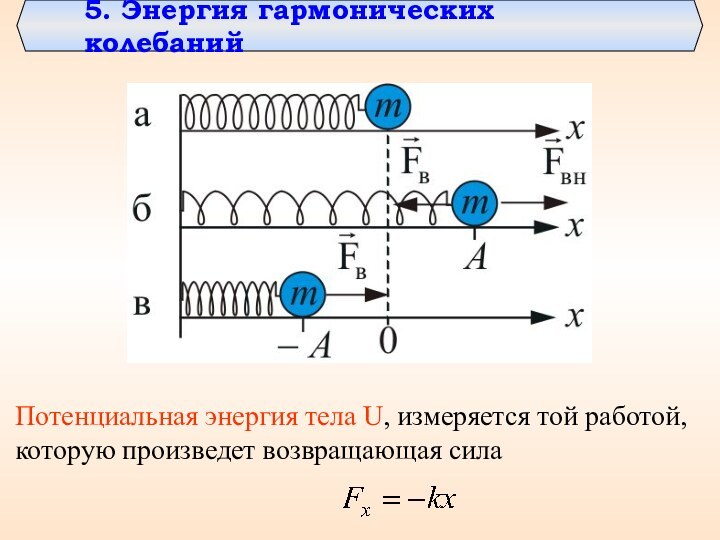
- 25. 5. Энергия гармонических колебанийПотенциальная энергия тела U, измеряется той работой, которую произведет возвращающая сила
- 26. , отсюда Кинетическая энергияПолная энергия:Полная механическая энергия гармонически колеблющегося тела пропорциональна квадрату амплитуды колебания. Потенциальная энергия
- 27. Колебания груза под действием сил тяжестиМаксимум потенциальной энергии, Максимум кинетической энергии
- 28. При колебаниях совершающихся
- 29. 6. Гармонический осциллятор1. Пружинный маятник – это
- 30. или циклическая частота ω
- 31. 2 Математическим маятником – называется идеализированная система,
- 32. Тогда , или Обозначим : - Это
- 33. 3 Физический маятник – это твердое тело,
- 34. - угловое ускорение, тогда
- 35. Все приведенные соотношения для математического и
- 36. 7. Способы представления гармонических колебанийГармонические колебания можно
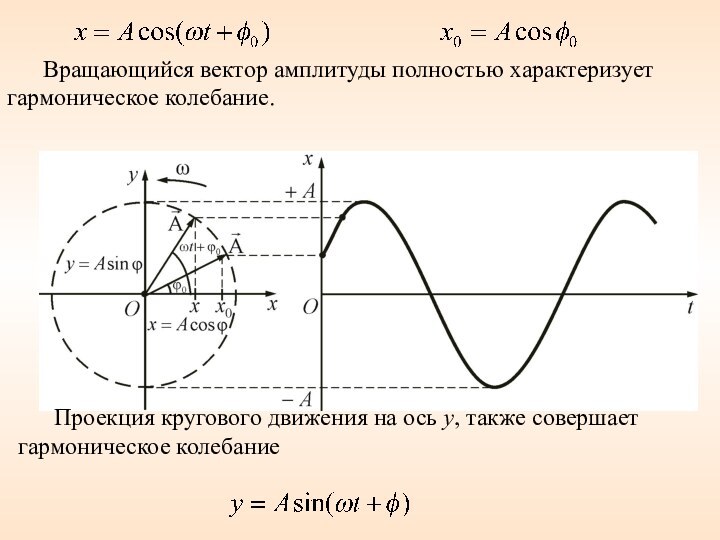
- 37. Геометрический способ, с помощью вектора амплитуды (метод векторных диаграмм).Ox – опорная прямая
- 38. Вращающийся вектор амплитуды полностью
- 39. 8. Сложение гармонических колебаний. БиенияКруговая волна на
- 40. Пусть точка одновременно участвует в двух гармонических
- 41. Ox – опорная прямаяA1 – амплитуда
- 42. По правилу сложения векторов найдем суммарную амплитуду,
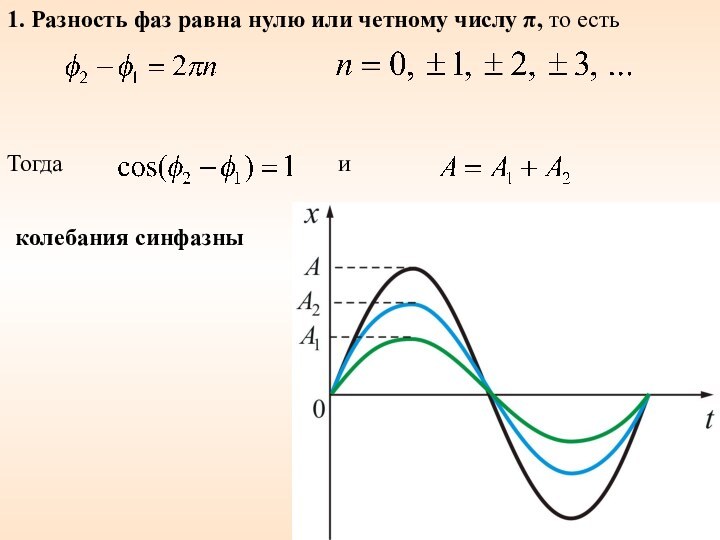
- 43. 1. Разность фаз равна нулю или четному числу π, то есть Тогда и колебания синфазны
- 44. 2. Разность фаз равна нечетному числу π, то есть , где Тогда колебания в противофазе
- 45. 3. Разность фаз изменяется во времени произвольным
- 46. Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биениями.
- 47. Слагаемые ряда Фурье, определяющие
- 48. 9. Сложение взаимно перпендикулярных колебанийВ результате получили уравнение эллипса с произвольно расположенными осями
- 49. 10. Фигуры Лиссажу1. Начальные фазы колебаний одинаковыЭто уравнение прямой, проходящей через начало координат
- 50. 2. Начальная разность фаз равна π.
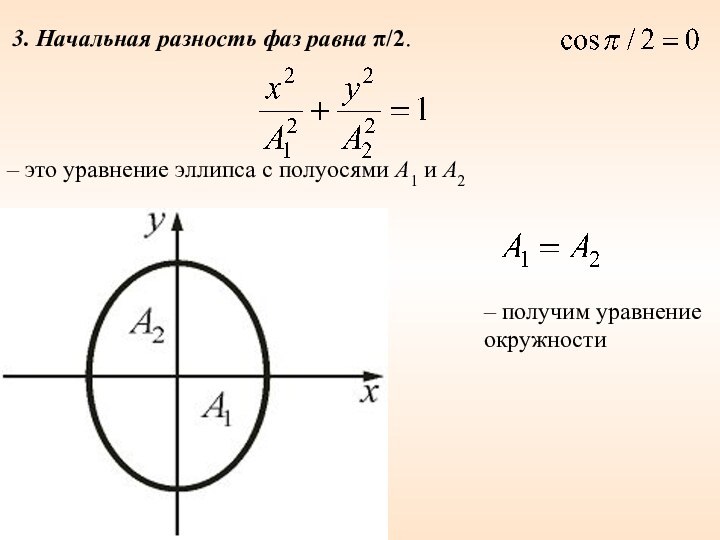
- 51. 3. Начальная разность фаз равна π/2. –
- 52. 4. Все остальные разности фаз
- 53. Фигуры Лиссажу
- 54. 11. Свободные затухающие механические колебания Все
- 55. Второй закон Ньютона для затухающих прямолинейных колебаний
- 56. Найдем частоту колебаний ω. ;;Условный периодРешение уравнения имеет вид
- 57. 12. Коэффициент затухания и логарифмический декремент затуханиягде β – коэффициент затухания
- 58. Логарифмическим декрементом затухания называется
- 59. Когда сопротивление становится равным критическомуто круговая частота
- 60. 13. Вынужденные механические колебания Рассмотрим
- 61. Уравнение установившихся вынужденных колебаний Задача
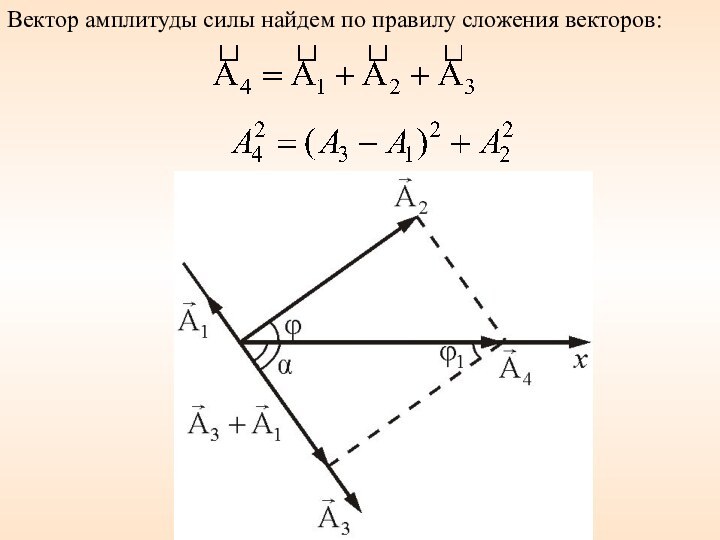
- 62. Вектор амплитуды силы найдем по правилу сложения векторов:
- 63. 1)(частота вынуждающей силы равна нулю) – статическая
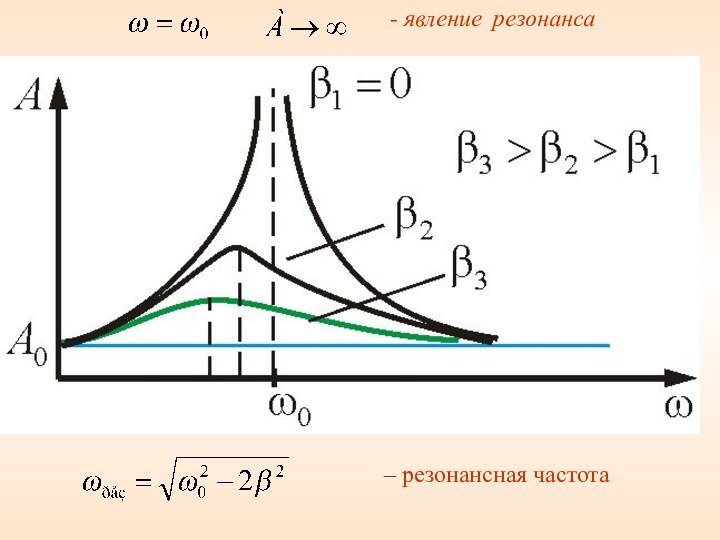
- 64. - явление резонанса – резонансная частота
- 65. – резонансная частота. Явление возрастания амплитуды
- 66. Принцип работы всех автоколебательных систем
- 67. Скачать презентацию
- 68. Похожие презентации








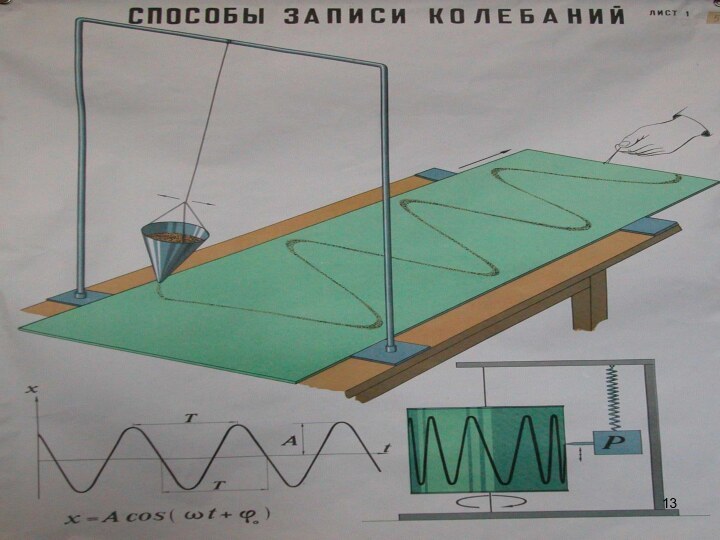
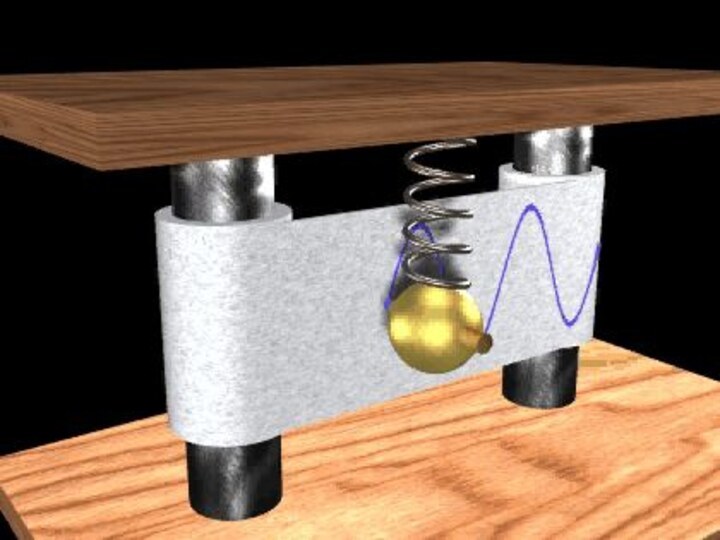




























Слайд 2
Примеры колебательных процессов
Круговая волна на
поверхности жидкости, возбуждаемая точечным источником (гармонически колеблющимся шариком).
Генерация акустической волны громкоговорителем.Слайд 3 Возможные типы колебаний атомов в
кристалле.
Поперечная волна в сетке, состоящей
из шариков, скреплённых пружинками. Колебания масс происходят перпендикулярно направлению распространения волны.Примеры колебательных процессов
Слайд 4
1. Виды и признаки колебаний
Колебания делятся на механические
и электромагнитные (электромеханические комбинации)
Для колебаний характерно превращение одного вида
энергии в другую – кинетической в потенциальную, магнитной в электрическую и т.д.Колебательным движением (или просто колебанием) называются процессы, повторяющиеся во времени.
Слайд 5
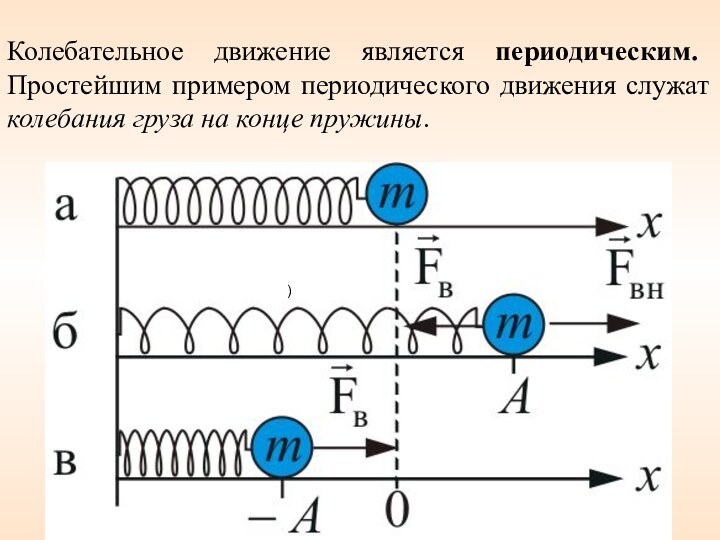
Колебательное движение является периодическим. Простейшим
примером периодического движения служат колебания груза на конце пружины.
)
Слайд 6
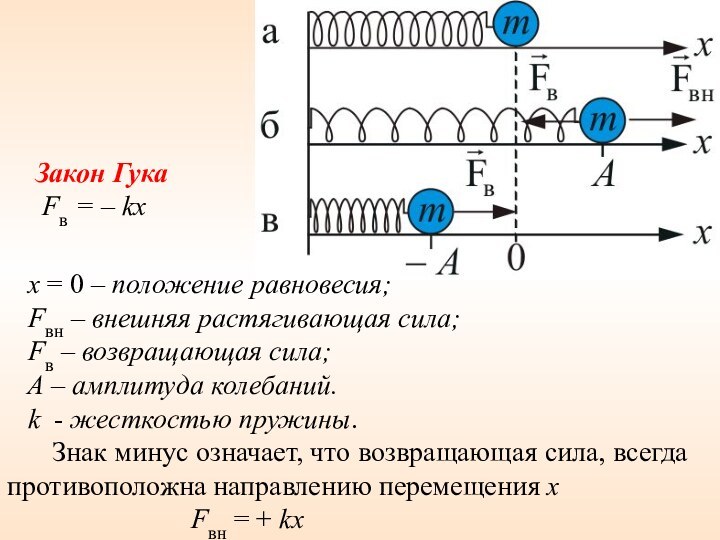
x = 0 – положение равновесия;
Fвн – внешняя растягивающая сила;
Fв
– возвращающая сила; A – амплитуда колебаний.
k - жесткостью пружины.
Знак минус означает, что возвращающая сила, всегда противоположна направлению перемещения x
Fвн = + kx
Закон Гука
Fв = – kx
Слайд 7
Три признака колебательного движения:
повторяемость (периодичность) – движение по
одной и той же траектории туда и обратно;
ограниченность пределами
крайних положений;действие силы, описываемой функцией F = – kx.
Слайд 9 Колебания называются периодическими, если значения
физических величин, изменяющихся в процессе колебаний, повторяются через равные
промежутки времени.Простейшим типом периодических колебаний являются так называемые гармонические колебания.
Любая колебательная система, в которой возвращающая сила прямо пропорциональна смещению, взятому с противоположным знаком (например, F = – kx), совершает гармонические колебания.
Саму такую систему часто называют гармоническим осциллятором.
Слайд 10 Различные периодические процессы (повторяющиеся через равные промежутки
времени) можно представить как наложение гармонических колебаний.
Периодический процесс можно описать уравнением:Колебания называются гармоническими, если зависимость некоторой величины имеет вид
или
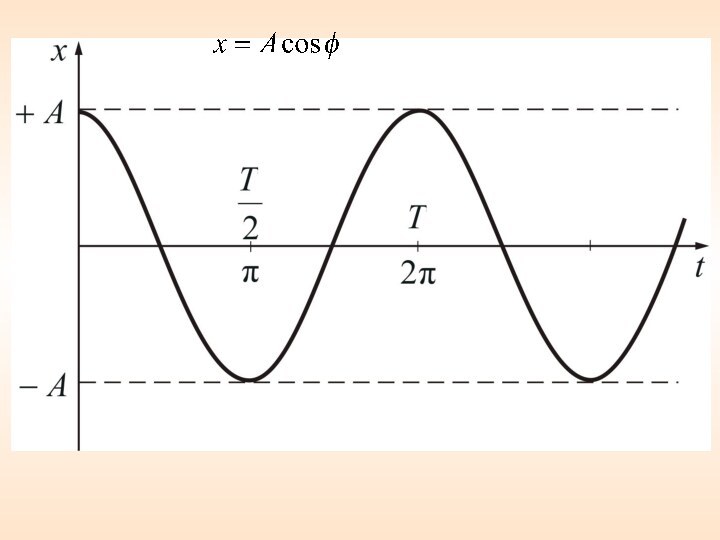
Слайд 11 Расстояние груза от положения равновесия до точки,
в которой находится груз, называют смещением x.
Максимальное смещение
– наибольшее расстояние от положения равновесия – называется амплитудой и обозначается, буквой A. определяет смещение x в данный момент времени t и называется фазой колебания.
называется начальной фазой колебания при t=0
2. Параметры гармонических колебаний
.
Слайд 15 Частота колебаний ν определяется, как число полных колебаний
в 1 секунду. Частоту, измеряют в герцах (Гц):
1
Гц = 1 колебание в секунду. Период колебаний Т – минимальный промежуток времени, по истечении которого повторяются значения всех физических величин, характеризующих колебание
Слайд 16 ω – циклическая (круговая) частота –
число полных колебаний за 2π секунд.
Фаза φ
не влияет на форму кривой х(t), а влияет лишь на ее положение в некоторый произвольный момент времени t. Гармонические колебания являются всегда синусоидальными.
Частота и период гармонических колебаний не зависят от амплитуды.
Слайд 17
– амплитуда скорости;
– амплитуда ускорения.
Смещение описывается уравнением
тогда, по определению:
скорость
ускорение
Слайд 20 Скорость колебаний тела максимальна и равна
амплитуде скорости в момент прохождения через положение равновесия
(x=0).При максимальном смещении ( ) скорость равна нулю.
Ускорение равно нулю при прохождении телом положения равновесия и достигает наибольшего значения, равного амплитуде ускорения при наибольших смещениях.
Слайд 21 Найдем разность фаз φ между фазами смещения х
и скорости υx.
то есть скорость опережает смещение на
π/2.Аналогично можно показать, что ускорение в свою очередь опережает скорость по фазе на π/2:
Тогда ускорение опережает смещение на π, или
то есть, смещение и ускорение находятся в противофазе
Слайд 22
4. Основное уравнение динамики гармонических
колебаний
Исходя из
второго закона,
, можно записатьсила F пропорциональна х и всегда направлена к положению равновесия (поэтому ее и называют возвращающей силой).
Примером сил являются упругие силы. Силы же имеющие иную природу называются квазиупругими. Квазиупругая сила
где k – коэффициент квазиупругой силы.
Слайд 23 Получим основное уравнение динамики гармонических колебаний, вызываемых упругими
силами:
или
; , тогда Решение этого уравнения всегда будет выражение вида
Основное уравнение динамики гармонических колебаний
Слайд 25
5. Энергия гармонических колебаний
Потенциальная энергия тела U, измеряется
той работой, которую произведет возвращающая сила
Слайд 26
, отсюда
Кинетическая энергия
Полная энергия:
Полная механическая энергия гармонически
колеблющегося тела пропорциональна квадрату амплитуды колебания.
Потенциальная энергия
Слайд 27 Колебания груза под действием сил
тяжести
Максимум потенциальной энергии,
Максимум кинетической энергии
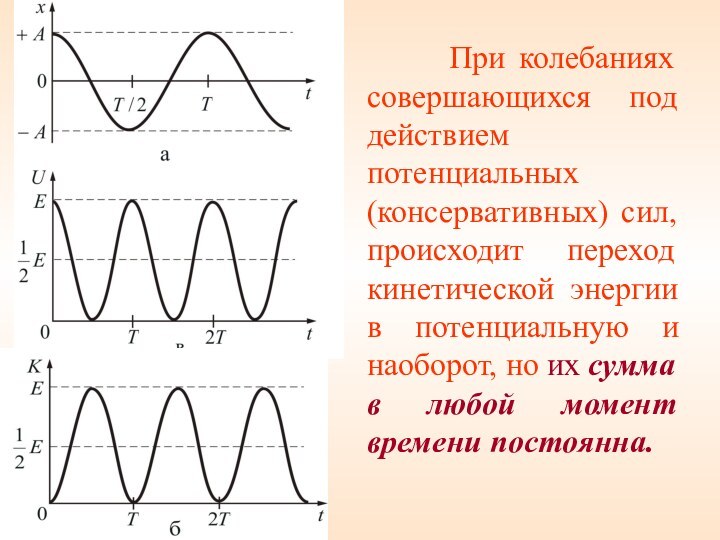
Слайд 28 При колебаниях совершающихся под
действием потенциальных (консервативных) сил, происходит переход кинетической энергии в
потенциальную и наоборот, но их сумма в любой момент времени постоянна.
Слайд 29
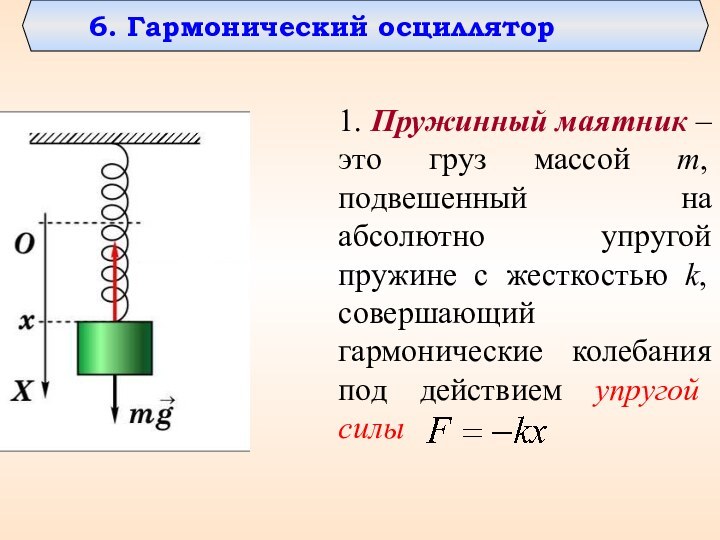
6. Гармонический осциллятор
1. Пружинный маятник – это груз
массой m, подвешенный на абсолютно упругой пружине с жесткостью
k, совершающий гармонические колебания под действием упругой силы
Слайд 30
или
циклическая частота ω
период Т
Из второго закона Ньютона
F = mа; или F = - kxполучим уравнение движения маятника:
Решение этого уравнения – гармонические колебания вида:
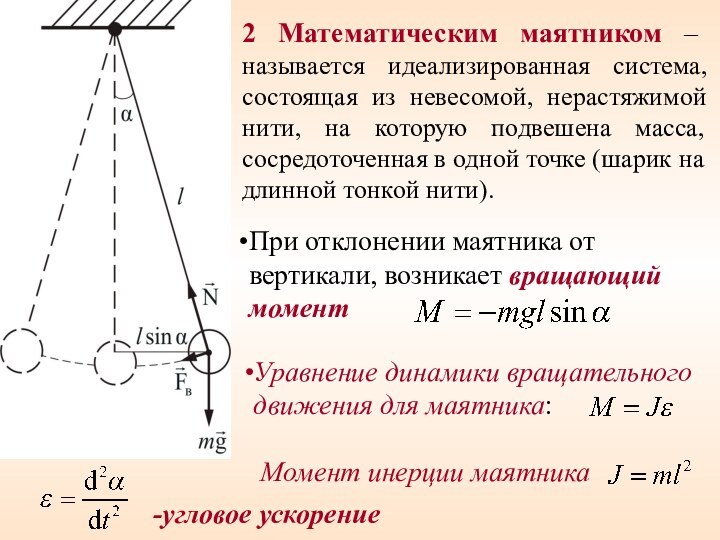
Слайд 31 2 Математическим маятником – называется идеализированная система, состоящая
из невесомой, нерастяжимой нити, на которую подвешена масса, сосредоточенная
в одной точке (шарик на длинной тонкой нити).При отклонении маятника от вертикали, возникает вращающий момент
Уравнение динамики вращательного движения для маятника:
Момент инерции маятника
-угловое ускорение
Слайд 32
Тогда
, или
Обозначим
:
- Это уравнение
динамики гармонических колебаний.
Решение уравнения имеет вид:
Т –
зависит только от длины маятника и ускорения свободного падения. Уравнение движения маятника
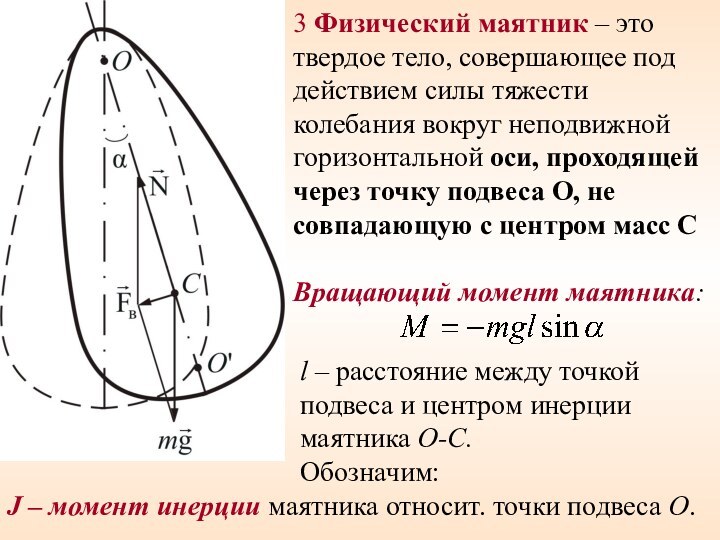
Слайд 33 3 Физический маятник – это твердое тело, совершающее
под действием силы тяжести колебания вокруг неподвижной горизонтальной оси,
проходящей через точку подвеса О, не совпадающую с центром масс СВращающий момент маятника:
l – расстояние между точкой подвеса и центром инерции маятника О-С.
Обозначим:
J – момент инерции маятника относит. точки подвеса O.
Слайд 34
- угловое ускорение, тогда
Уравнение
динамики вращательного движения
– приведенная длина физического
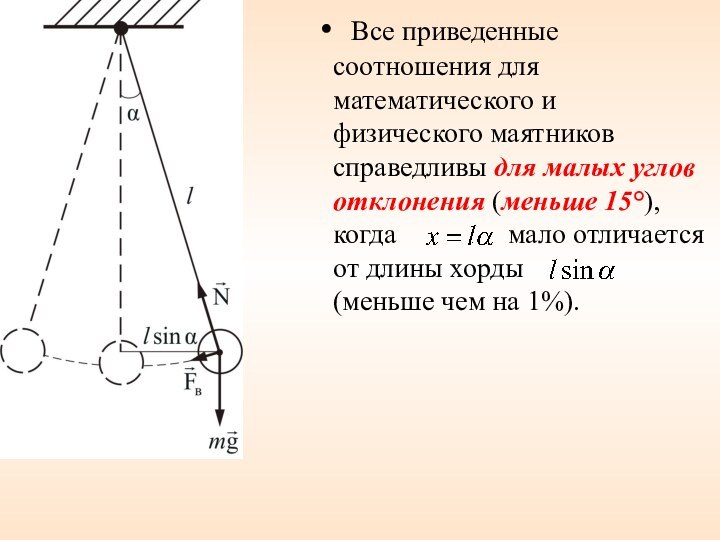
маятника – это длина такого математического маятника, период колебания которого совпадает с периодом колебаний данного физического маятника. Слайд 35 Все приведенные соотношения для математического и физического
маятников справедливы для малых углов отклонения (меньше 15°), когда
мало отличается от длины хорды (меньше чем на 1%).
Слайд 36
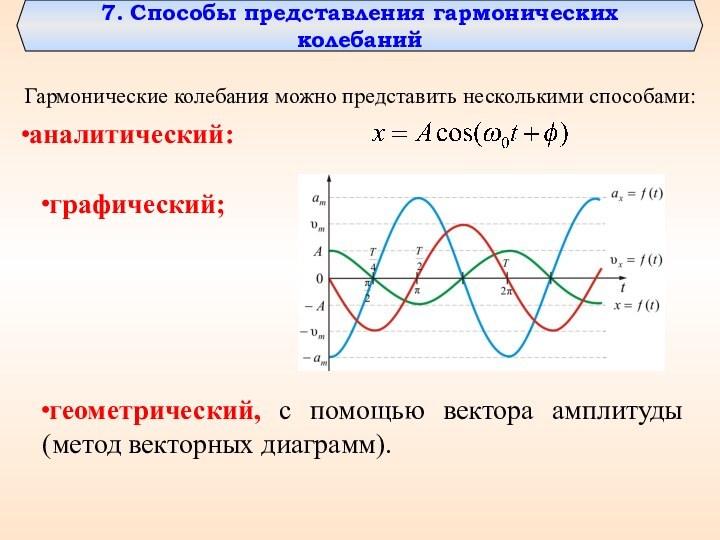
7. Способы представления гармонических колебаний
Гармонические колебания можно представить
несколькими способами:
аналитический:
графический;
геометрический, с помощью вектора амплитуды (метод векторных
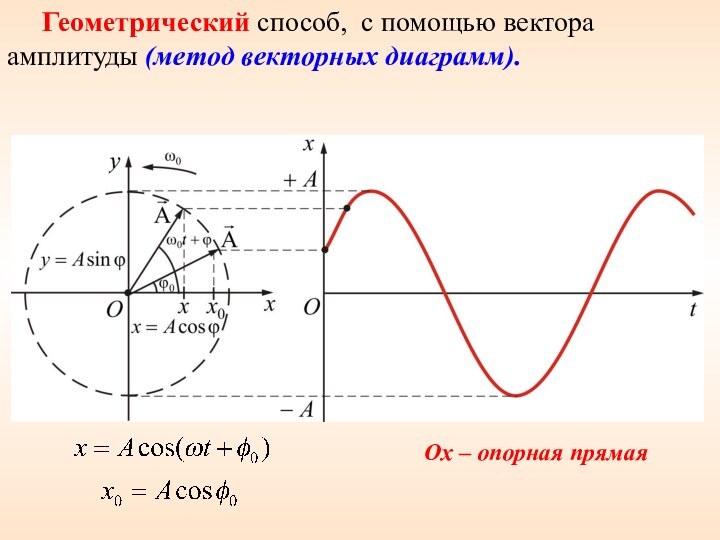
диаграмм).Слайд 37 Геометрический способ, с помощью вектора амплитуды (метод векторных
диаграмм).
Ox – опорная прямая
Слайд 38 Вращающийся вектор амплитуды полностью характеризует
гармоническое колебание.
Проекция кругового движения на
ось у, также совершает гармоническое колебание
Слайд 39
8. Сложение гармонических колебаний. Биения
Круговая волна на поверхности
жидкости, возбуждаемая гармонически колеблющимся шариком.
Интерференция между двумя круговыми
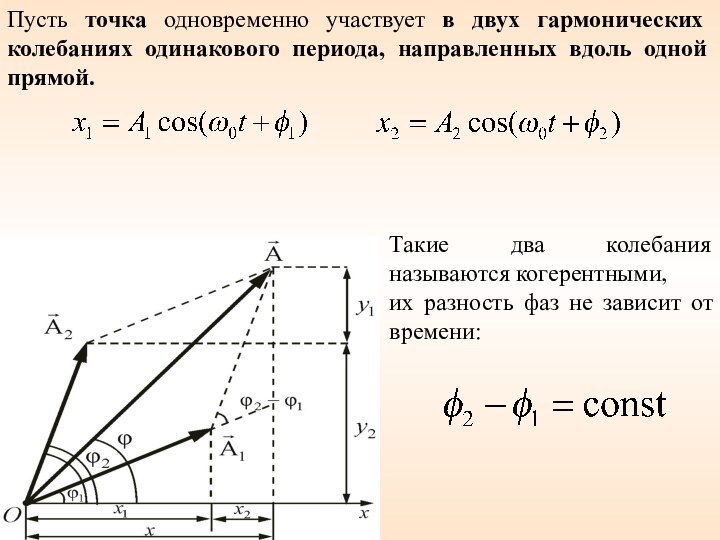
волнами от точечных источников, колеблющихся в фазе друг с другом. На поверхности жидкости образуются узловые линии, в которых колебание максимально или отсутствует. Слайд 40 Пусть точка одновременно участвует в двух гармонических колебаниях
одинакового периода, направленных вдоль одной прямой.
Такие два колебания
называются когерентными, их разность фаз не зависит от времени:
Слайд 41
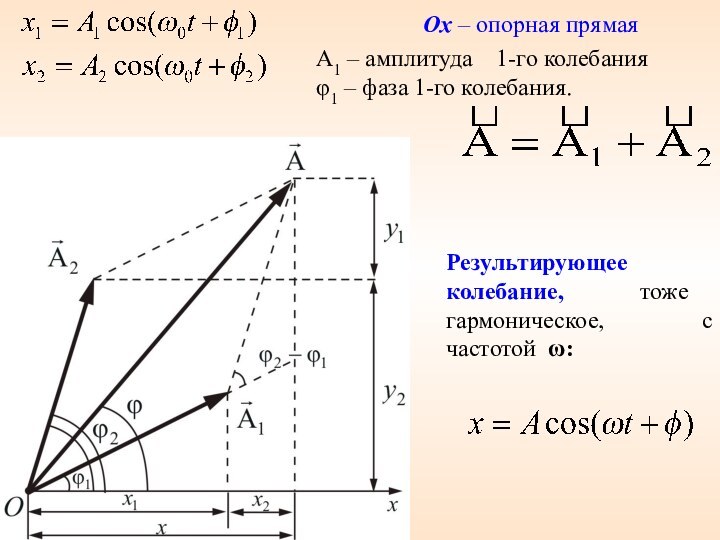
Ox – опорная прямая
A1 – амплитуда 1-го
колебания
φ1 – фаза 1-го колебания.
Результирующее колебание, тоже гармоническое, с
частотой ω:Слайд 42 По правилу сложения векторов найдем суммарную амплитуду, результирующего
колебания:
Начальная фаза определяется из соотношения
Амплитуда А результирующего
колебания зависит от разности начальных фаз Слайд 45 3. Разность фаз изменяется во времени произвольным образом
Это некогерентные колебания
Здесь интересен случай, называемый биениями, когда
частоты близки
Слайд 46 Периодические изменения амплитуды колебания, возникающие при сложении двух
гармонических колебаний с близкими частотами, называются биениями.
Слайд 47 Слагаемые ряда Фурье, определяющие гармонические
колебания с частотами ω, 2ω, 3ω, ..., называются первой
(или основной), второй, третьей и т.д. гармониками сложного периодического колебания.Любые сложные периодические колебания можно представить в виде суперпозиции одновременно совершающихся гармонических колебаний с различными амплитудами, начальными фазами, а также частотами кратными циклической частоте ω:
Слайд 48
9. Сложение взаимно перпендикулярных колебаний
В результате получили уравнение
эллипса с произвольно расположенными осями
Слайд 49
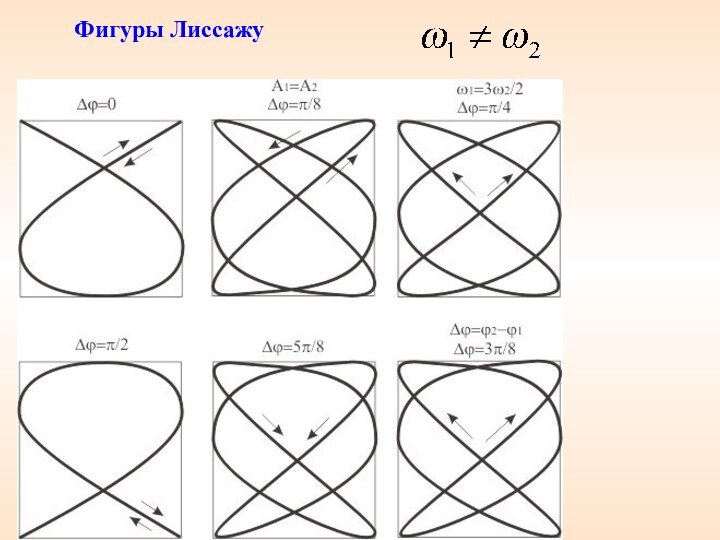
10. Фигуры Лиссажу
1. Начальные фазы колебаний одинаковы
Это уравнение
прямой, проходящей через начало координат
Слайд 51
3. Начальная разность фаз равна π/2.
– получим
уравнение окружности
– это уравнение эллипса с полуосями А1 и
А2
Слайд 52 4. Все остальные разности фаз дают
эллипсы с различным углом наклона относительно осей координат.
Фигуры, получаемые при сложении взаимно перпендикулярных колебаний разных частот, называются фигурами Лиссажу.
Слайд 54
11. Свободные затухающие механические колебания
Все реальные
колебания являются затухающими. Энергия механических колебаний постепенно расходуется на
работу против сил трения и амплитуда колебаний уменьшается.Сила трения (или сопротивления)
где r – коэффициент сопротивления,
Слайд 55 Второй закон Ньютона для затухающих прямолинейных колебаний вдоль
оси x
где kx – возвращающая сила,
– сила трения. Введем обозначения
)
Слайд 57
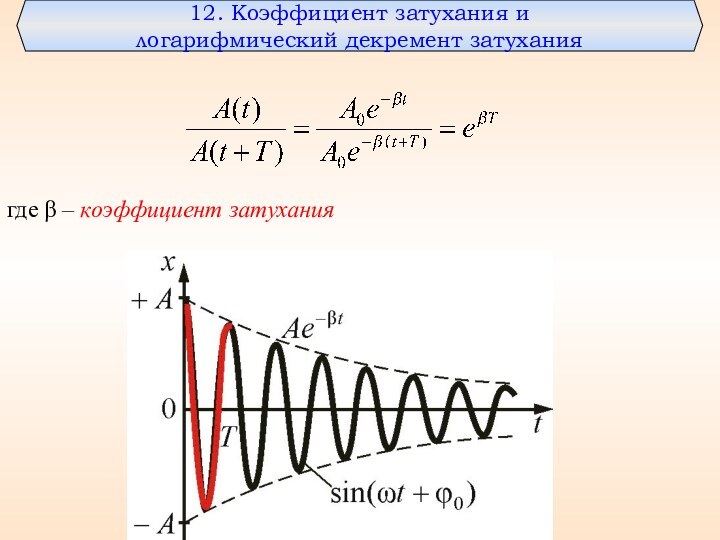
12. Коэффициент затухания и
логарифмический декремент затухания
где β
– коэффициент затухания
Слайд 58 Логарифмическим декрементом затухания называется натуральный
логарифм отношения амплитуд, следующих друг за другом через период
Т. Следовательно, коэффициент затухания β – есть физическая величина, обратная времени, в течение которого амплитуда уменьшается в е раз,
τ – время релаксации.
Слайд 59
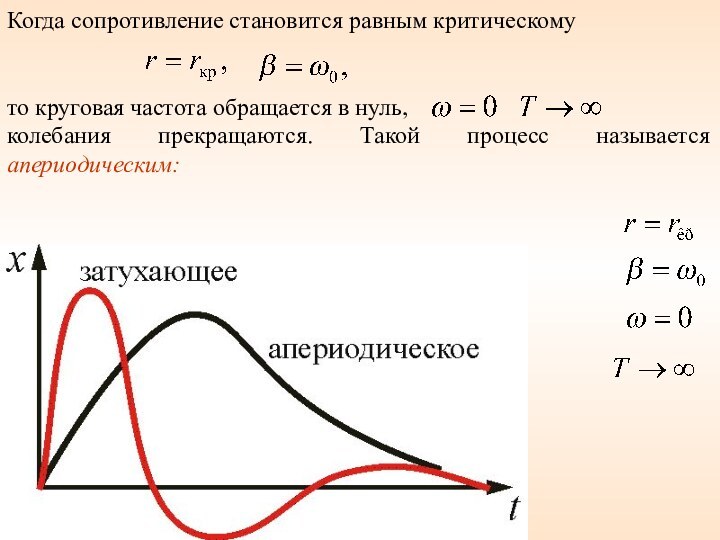
Когда сопротивление становится равным критическому
то круговая частота обращается
в нуль,
колебания прекращаются. Такой процесс называется апериодическим:
Слайд 60
13. Вынужденные механические колебания
Рассмотрим систему,
на которую кроме упругой силы (– kx) и сил
сопротивления (– rυ) действует добавочная периодическая сила F – вынуждающая сила:– основное уравнение колебательного процесса, при вынужденных колебаниях
Слайд 61
Уравнение установившихся вынужденных колебаний
Задача найти
амплитуду А и разность фаз φ между смещением вынужденных
колебаний и вынуждающей силой.– амплитуда ускорения;
– амплитуда скорости;
– амплитуда смещения;
– амплитуда вынуждающей силы
Введем обозначения:
Слайд 63
1)
(частота вынуждающей силы равна нулю)
– статическая амплитуда,
колебания не совершаются.
2)
(затухания нет). С увеличением ω (но при
),
амплитуда растет и при, амплитуда
резко возрастает (
). Это явление называется
– резонанс. При дальнейшем увеличении (
)
амплитуда опять уменьшается.
3) – резонансная частота
Слайд 65
– резонансная частота.
Явление возрастания амплитуды
вынужденных колебаний при приближении частоты вынуждающей силы к называется
резонансом. С увеличением коэффициента затухания β явление резонанса проявляется все слабее и исчезает при
Слайд 66
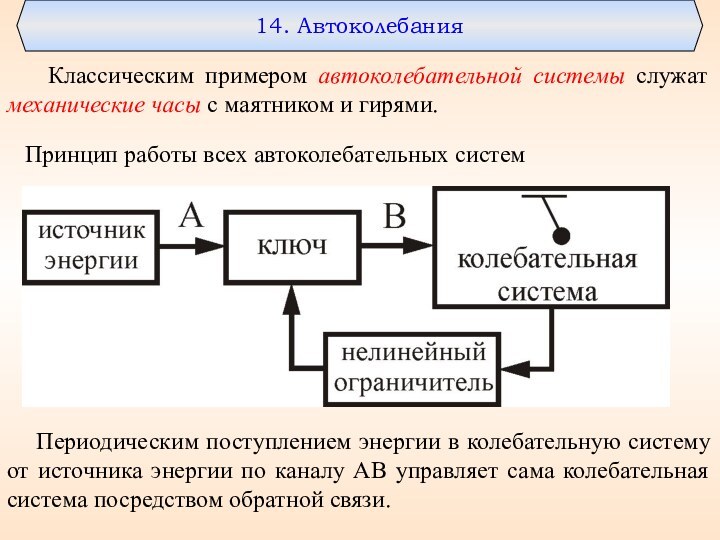
Принцип работы всех автоколебательных систем
Периодическим поступлением энергии в колебательную систему от источника энергии
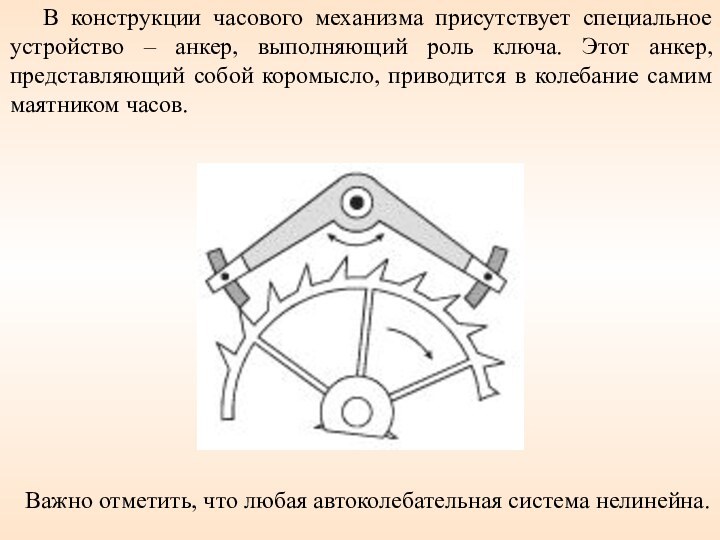
по каналу АВ управляет сама колебательная система посредством обратной связи.14. Автоколебания
Классическим примером автоколебательной системы служат механические часы с маятником и гирями.





























