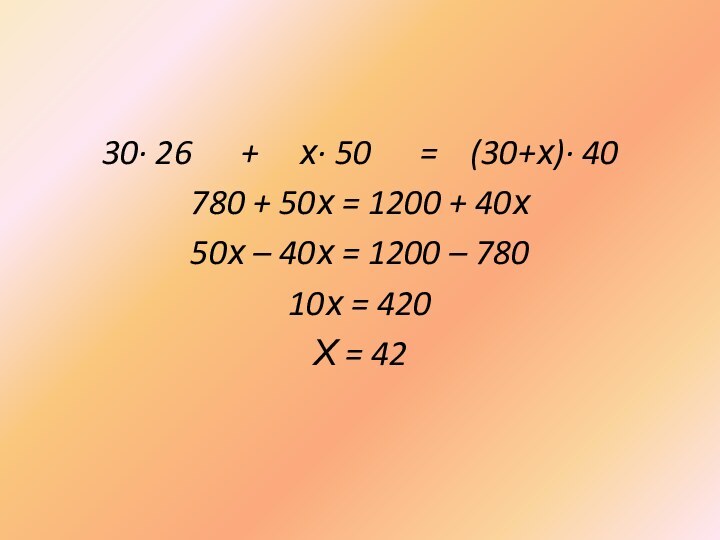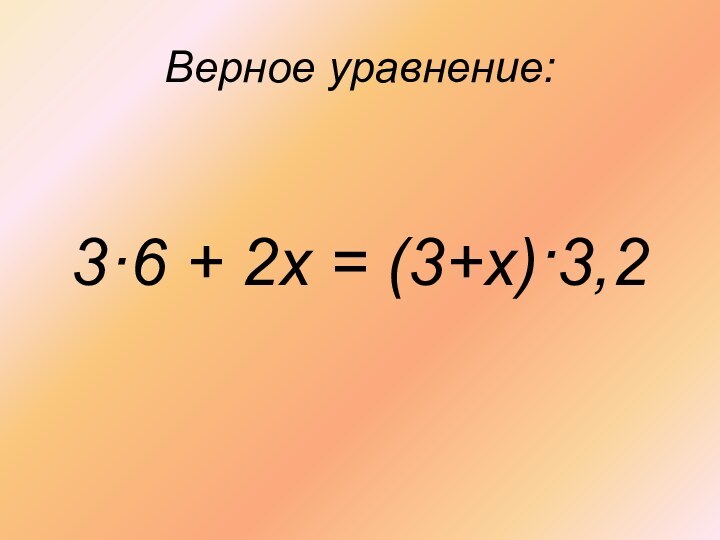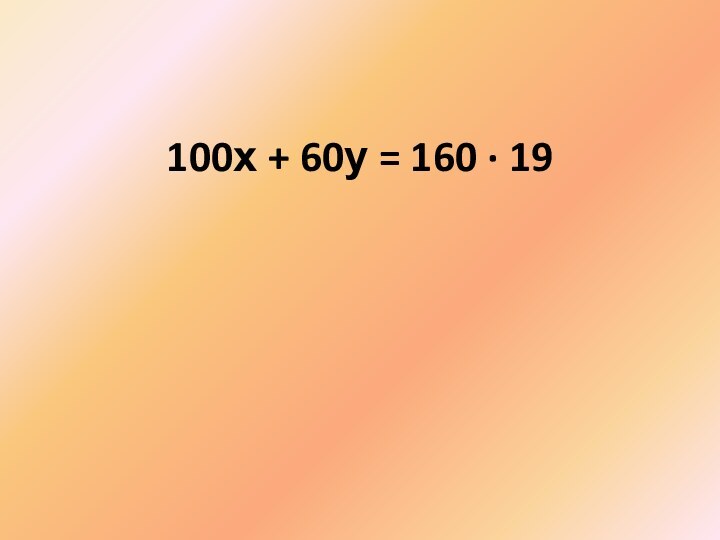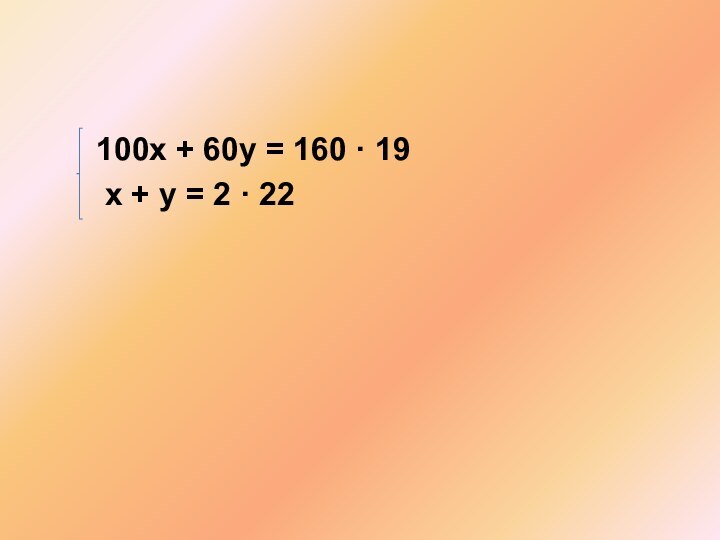Слайд 2
ПОВТОРИМ:
1) Представим в виде дроби проценты:
а) 50% б) 43% в)125% г)
4,2%
50% = 0,5, 43% = 0,43, 125% = 1,25, 4,2% = 0,042
2) Отношение чисел - это частное этих чисел. Найти отношение числа 20 к 80
20 : 80 = 0,25 или ¼.
3) Нахождение дроби от числа: чтобы найти дробь от числа, надо дробь умножить на число. 0,3 от 70 находится так: 0,3 · 70 = 21
3) Решение линейного уравнения:
0,25х + 0,13 (х+5) = 0,2 (2х+5)
Слайд 4
Возьмем 180 граммов воды и добавим в воду
20 граммов соли. Получим раствор соли, его масса равна
180 + 20 = 200 граммов.
Концентрация соли
(процентное содержание соли) - это отношение количества
соли к количеству раствора, записанное в процентах -
(20 : 200) ·100 = 10%
Слайд 5
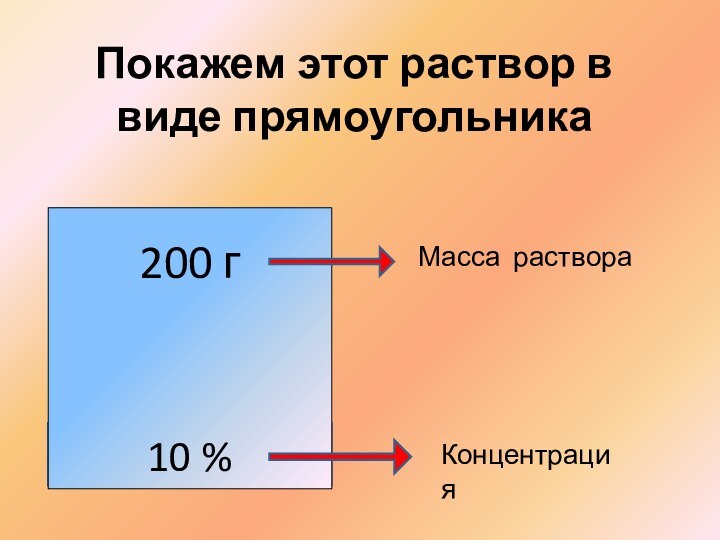
Покажем этот раствор в виде прямоугольника
200 г
10 %
Масса раствора
Концентрация
Слайд 6
Возьмем 15 кг цемента и 45 кг песка,
высыпаем содержимое ведер в ящик и тщательно перемешаем цемент
с песком. Получим смесь цемента с песком, её масса равна 15 кг + 45 кг = 60 кг.
Концентрация цемента (процентное содержание цемента) – это отношение количества цемента к количеству смеси, записанное в процентах –
(15 : 60)·100 = 25%
Слайд 7
Покажем эту смесь в виде прямоугольника
60 кг
25 %
Слайд 8
смешали, перемешали: «+»
отлили: «-»
долили, добавили: «+»
Слайд 9
Закон сохранения объема или массы
Если два сплава (раствора)
соединяют в один «новый» сплав (раствор), то
V = V1 + V2 – сохраняется объем;
m = m1+ m2 – сохраняется масса. Причем сохраняется масса не только раствора, но и чистого вещества.
Слайд 10
Например, смешали раствор воды с песком, в котором
4кг песка и 10кг воды, с другим раствором, в
котором 10кг песка и 20кг воды. Какова масса полученного раствора? (44кг) Какова масса песка в полученном растворе? (14кг)
Слайд 11
Задача №1
Имеется 30кг 26%-го раствора соли. Требуется получить
40%-ый раствор соли. Сколько килограммов 50%-го раствора соли нужно
добавить?
Слайд 12
Задача №1
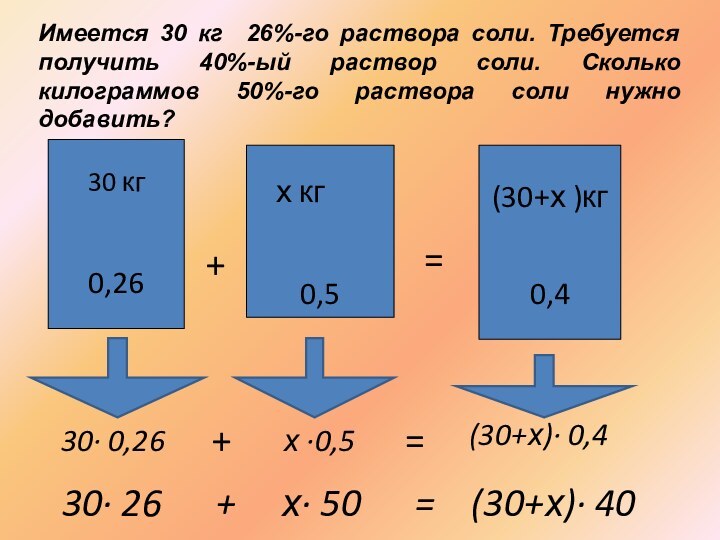
Имеется 30 кг 26%-го раствора соли. Требуется
получить 40%-ый раствор соли. Сколько килограммов 50%-го раствора соли
нужно добавить?
30 кг
26 %
50 %
40 %
Имеется
Нужно добавить
Требуется получить
=
+
х кг
(30+х )кг
30 кг
0,26
0,5
0,4
=
+
х кг
(30+х )кг
30· 0,26
х ·0,5
(30+х)· 0,4
=
+
30· 26 + х· 50 = (30+х)· 40
Имеется 30 кг 26%-го раствора соли. Требуется получить 40%-ый раствор соли. Сколько килограммов 50%-го раствора соли нужно добавить?
Слайд 14
Таким образом, алгоритм составления уравнения следующий:
по вертикали
из каждого прямоугольника находим массу чистого вещества, умножив массу
или объем на концентрацию;
по горизонтали составляем уравнение согласно действиям в схеме.
50 = (30+х)· 40
780 + 50х
= 1200 + 40х
50х – 40х = 1200 – 780
10х = 420
Х = 42
Слайд 16
Задача №2
В бидоне было 3 литра молока
6%-ой жирности. После того как в бидон добавили некоторое
количество молока 2%-ой жирности и тщательно перемешали, получили молоко с жирностью 3,2%. Сколько литров молока 2%-ой жирности было добавлено в бидон?
Слайд 17
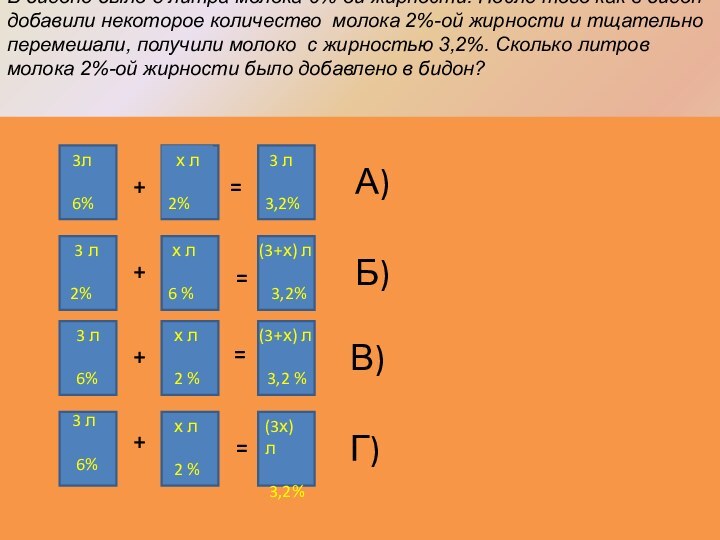
В бидоне было 3 литра молока 6%-ой жирности.
После того как в бидон добавили некоторое количество молока
2%-ой жирности и тщательно перемешали, получили молоко с жирностью 3,2%. Сколько литров молока 2%-ой жирности было добавлено в бидон?
3л
6%
3 л
6%
(3+х) л
3,2%
х л
6 %
3 л
2%
х л
2%
3 л
3,2%
х л
2 %
3 л
6%
(3+х) л
3,2 %
х л
2 %
(3х) л
3,2%
+
=
+
=
+
+
=
=
А)
Г)
В)
Б)
Слайд 18
Верное уравнение:
3·6 + 2х = (3+х)·3,2
Слайд 19
Задача №3
Из чаши, содержащей 300 граммов 6%-го раствора
уксусной кислоты, отлили некоторое количество этого раствора и добавили
такое же количество воды. Определите, сколько граммов воды было добавлено, если известно, что в результате получили 2%-ый раствор уксусной кислоты.
Было
Отлили
Добавили
Получили
Слайд 21
Из чаши, содержащей 300 граммов 6%-го раствора уксусной
кислоты, отлили некоторое количество этого раствора и добавили такое
же количество воды. Определите, сколько граммов воды было добавлено, если известно, что в результате получили 2%-ый раствор уксусной кислоты.
300 г
6%
Было
Отлили
Добавили
Получили
х г
6%
х г
0%
300 г
2%
-
=
+
300 · 6 – 6х + х·0 = 300 · 2
Ответ: 200 г.
21 л
10%
7 л
10%
0%
17,5 л
х%
+
-
=
Слайд 26
Задача №5
Имеется кусок сплава меди с оловом общей
массой 24 кг, содержащий 45% меди. Сколько чистого олова
надо прибавить к этому куску сплава, чтобы полученный новый сплав содержал 40% меди?
Слайд 27
Имеется кусок сплава меди с оловом общей массой
24 кг, содержащий 45% меди. Сколько чистого олова надо
прибавить к этому куску сплава, чтобы полученный новый сплав содержал 40% меди?
24 кг
45%
х кг
0%
24+х
40%
=
+
24 · 45 + х · 0 = 40(24 + х)
х = 3
Слайд 28
Задача №6
К раствору соляной кислоты добавили 100 г
соляной кислоты. В результате получили 600г 18%-го раствора соляной
кислоты. Сколько граммов соляной кислоты содержалось в исходном растворе?
Слайд 29
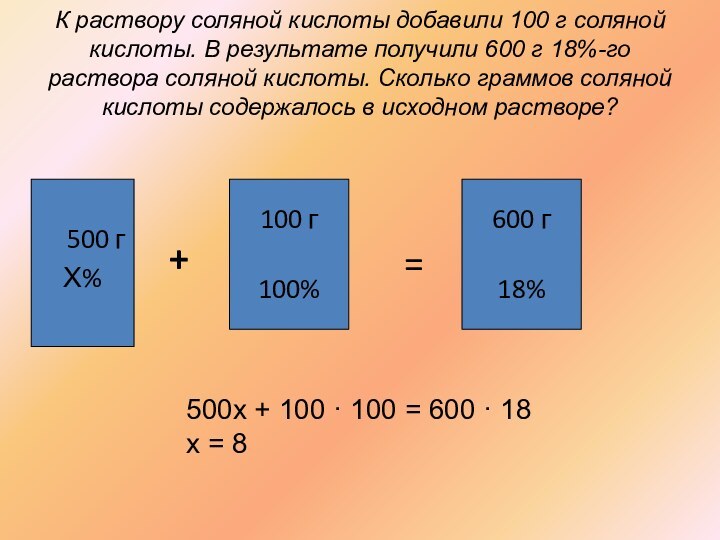
К раствору соляной кислоты добавили 100 г соляной
кислоты. В результате получили 600 г 18%-го раствора соляной
кислоты. Сколько граммов соляной кислоты содержалось в исходном растворе?
500 г
Х%
100 г
100%
600 г
18%
+
=
500х + 100 · 100 = 600 · 18
х = 8
Слайд 30
Задача №7
Сплавили два слитка серебра: 75 г 600-й
пробы и 150 г 864-й пробы. Определить пробу сплава.
Слайд 31
Сплавили два слитка серебра: 75 г 600-й и
150 г 864-й пробы. Определить пробу сплава.
75 г
600
150 г
864
225 г
х
=
+
75·600 + 150 · 864 = 225 · х
х = 776
Слайд 32
Задача №8
Смешали некоторое количество 15%-го раствора некоторого вещества
с таким же количеством 19%-го раствора этого же вещества.
Сколько процентов составляет концентрация получившегося раствора?
Слайд 33
Смешали некоторое количество 15%-го раствора некоторого вещества с
таким же количеством 19%-го раствора этого же вещества. Сколько
процентов составляет концентрация получившегося раствора?
15%
19%
Х%
+
=
Слайд 34
Смешали некоторое количество 15%-го раствора некоторого вещества с
таким же количеством 19%-го раствора этого же вещества. Сколько
процентов составляет концентрация получившегося раствора?
у
15%
у
19%
2у
Х%
+
=
15у + 19у = 2ух
15 + 19 = 2х
х = 17
Слайд 35
Задача №9
Имеется два сосуда. Первый содержит
100 кг, а второй 60 кг раствора кислоты различной
концентрации. Если эти растворы смешать, то получится раствор, содержащий 19% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 22 % кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Слайд 36
Имеется два сосуда. Первый содержит 100 кг, а
второй 60 кг раствора кислоты различной концентрации. Если эти
растворы смешать, то получится раствор, содержащий 19% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 22 % кислоты. Сколько килограммов кислоты содержится в первом сосуде?
100 кг
Х%
60 кг
у%
160 кг
19%
+
=
Слайд 38
Имеется два сосуда. Первый содержит 100 кг, а
второй 60 кг раствора кислоты различной концентрации. Если эти
растворы смешать, то получится раствор, содержащий 19% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 22 % кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Х%
у%
22%
+
=
Слайд 39
Имеется два сосуда. Первый содержит 100 кг, а
второй 60 кг раствора кислоты различной концентрации. Если эти
растворы смешать, то получится раствор, содержащий 19% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 22 % кислоты. Сколько килограммов кислоты содержится в первом сосуде?
р
Х%
р
у%
2р
22%
+
=
Слайд 42
Задача №10
Смешав 30%-ый и 60%-ый растворы кислоты и
добавив 10кг чистой воды, получили 36%-ый раствор кислоты. Если
бы вместо 10 кг воды добавили бы 10 кг 50%-ого раствора той же кислоты, то получили бы 41%-ый раствор кислоты. Сколько килограммов 30%-го раствора использовали для получения смеси?
Слайд 43
Смешав 30%-ый и 60%-ый растворы кислоты и добавив
10 кг чистой воды, получили 36%-ый раствор кислоты. Если
бы вместо 10 кг воды добавили бы 10 кг 50%-ого раствора той же кислоты, то получили бы 41%-ый раствор кислоты. Сколько килограммов 30%-го раствора использовали для получения смеси?
х кг
30%
у кг
60%
10 кг
0%
(х+у+10) кг
36%
+
=
+
30х +60у +10 · 0 = 36(х + у +10)
Слайд 44
Смешав 30%-ый и 60%-ый растворы кислоты и добавив
10 кг чистой воды, получили 36%-ый раствор кислоты. Если
бы вместо 10 кг воды добавили бы 10 кг 50%-ого раствора той же кислоты, то получили бы 41%-ый раствор кислоты. Сколько килограммов 30%-го раствора использовали для получения смеси?
х кг
30%
у кг
60%
10 кг
50%
(х+у+10) кг
41%
+
=
+
30х +60у +10 · 50 = 36(х + у +10)
Слайд 45
30х +60у +10 · 0 =
36(х + у +10)
30х +60у +10 · 50
= 36(х + у +10)
у=30, х=60.
Слайд 46
Задача №11
Влажность свежих грибов 90%, а сухих 15%.
Сколько сухих грибов получится из 1,7 кг свежих?
Слайд 47
Влажность свежих грибов 90%, а сухих 15%. Сколько
сухих грибов получится из 1,7 кг свежих?
свежие сухие
1,7 кг
10%
х кг
85%
=
1,7 · 10 = х ·85,
х =0,2
Слайд 48
Задача №12
Руда содержит 40% примесей, а выплавленный из
нее металл содержит 4% примесей. Сколько тонн руды необходимо
взять, чтобы выплавить из нее 15 тонн металла?
Слайд 49
Руда содержит 40% примесей, а выплавленный из нее
металл содержит 4% примесей. Сколько тонн руды необходимо взять,
чтобы выплавить из нее 15 тонн металла?
руда металл
х т
60%
15т
96%
=
60 · х = 15 · 96,
х =24
Слайд 50
Задача №13
Два сосуда со щелочью разных концентраций содержат
вместе 20 литров раствора. Первый сосуд содержит 4 л
щелочи, а второй – 6 л. Сколько процентов щелочи содержит первый сосуд, если второй содержит щелочи на 40% меньше первого?
Слайд 51
Два сосуда со щелочью разных концентраций содержат вместе
20 литров раствора. Первый сосуд содержит 4 л щелочи,
а второй – 6 л. Сколько процентов щелочи содержит первый сосуд, если второй содержит щелочи на 40% меньше первого?
20л
4 л
6 л