Презентация на тему Урок №3 Энергетический баланс для механической части электропривода

электропривода

1. Установившиеся режимы и устойчивость работы электропривода.

2. Уравнение движения электропривода.
3. Определение времени пуска и торможения электропривода.
4. Решение задач.
5. Домашнее задание.

Для работы двигателя и производственного

механизма в установившемся режиме должно существовать равновесие момента сопротивления механизма и вращательного момента двигателя при определенной скорости, т.е. М = Мс.
Изменение момента сопротивления на валу электродвигателя приводит к изменению скорости вращения двигателя и его момента – привод переходит автоматически в другое устойчивое состояние.Эта особенность присуща только электродвигателям и роль автоматического регулятора выполняет противо ЭДС двигателя. Привод статически устойчив, если в точке установив-
шегося режима выполняется условие
dM / dω - dMc / dω < 0 или β - βс < 0.
При постоянном моменте нагрузки статичес-
кая устойчивость будет определяться только
жесткостью механической характеристики дви-
гателя, т.к. в этом случае dMc / dω = 0,
(см. механическая характеристика ИО).

На приведенном слайде

точка А пересечения характеристик двигателя 1 и исполнительного механизма 2 соответствует установившемуся движению электропривода со скоростью ωуст. Если по какой то причине скорость ЭП повысилась до уровня ω1, то, как видно из характеристик, момент нагрузки Мс1 станет больше момента двигателя М1. Тогда в соответствии с уравнением
±М ± Мс = J•dω / dt в системе «двигатель – исполнительный механизм» будет действовать отрицательный динамический момент. Начнется процесс торможения до скорости ωуст.
Пусть по какой-то причине (кратковременное исчез-
новение напряжения) произошло снижение скорости до
ω2. В этом случае момент двигателя М2 превысит мо-
мент нагрузки Мс2 и положительный динамический мо-
мент начнет увеличивать скорость до ωуст

Если жесткость механической характеристики

двигателя отрицательна, то работа в установившемся режиме будет устойчива, т.к.
dM / dω - dMc / dω = dM / dω < 0,
что имеет место при работе привода в точке 1.
Если нагрузить двигатель и перевести его для работы в точку 2, то
dM / dω - dMc / dω = dM / dω > 0
и работа привода в этой точке станет неустойчивой.
При проектировании электропривода меха-
ническая характеристика производственного
механизма уже задана (известна).
Для устойчивой работы электропривода
остается подобрать механическую характе-
ристику двигателя соответствующей формы.
Это достигается подбором электродвигателя
соответствующего типа.

При переходе электропривода из одного установившегося режима

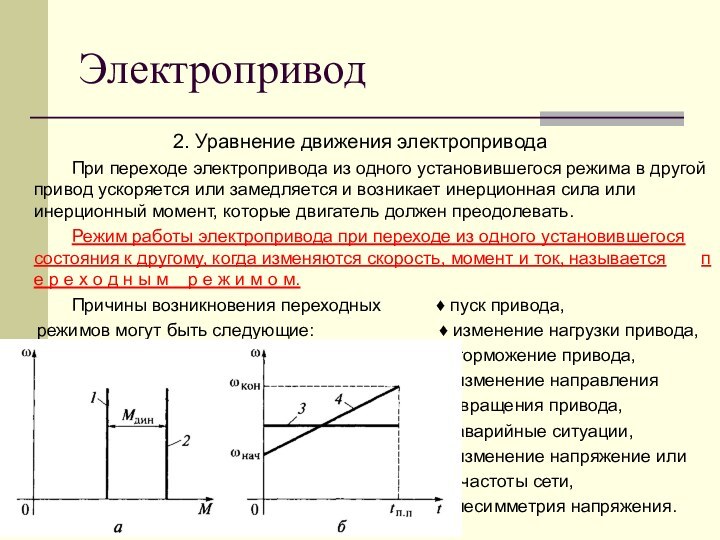
в другой привод ускоряется или замедляется и возникает инерционная сила или инерционный момент, которые двигатель должен преодолевать.
Режим работы электропривода при переходе из одного установившегося состояния к другому, когда изменяются скорость, момент и ток, называется п е р е х о д н ы м р е ж и м о м.
Причины возникновения переходных ♦ пуск привода,
режимов могут быть следующие: ♦ изменение нагрузки привода,
♦ торможение привода,
♦ изменение направления
вращения привода,
♦ аварийные ситуации,
♦ изменение напряжение или
частоты сети,
♦ несимметрия напряжения.

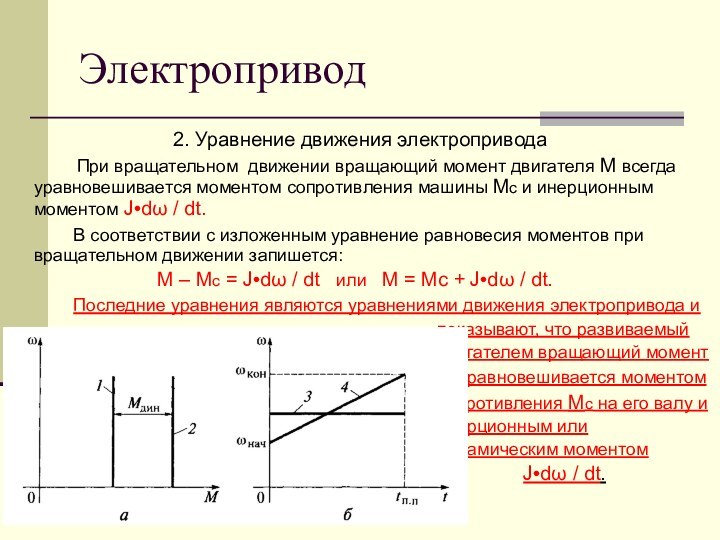
При вращательном движении вращающий момент двигателя М

всегда уравновешивается моментом сопротивления машины Мс и инерционным моментом J•dω / dt.
В соответствии с изложенным уравнение равновесия моментов при вращательном движении запишется:
М – Мс = J•dω / dt или М = Мс + J•dω / dt.
Последние уравнения являются уравнениями движения электропривода и
показывают, что развиваемый
двигателем вращающий момент
М уравновешивается моментом
сопротивления Мс на его валу и
инерционным или
динамическим моментом
J•dω / dt.

Анализ уравнений движения электропривода

М – Мс = J•dω / dt или М = Мс + J•dω / dt
показывает, что:
♦ при М > Мс J•dω / dt > 0, т.е. имеет место ускорение привода,
♦ при М < Мс J•dω / dt < 0, т.е. имеет место замедление привода,
♦ при М = Мс J•dω / dt = 0, в данном случае имеет место
установившийся режим.
Вращающий момент двигателя принимается положительным, если он направлен в сторону движения привода. Если он направлен в сторону обратную движению, то считается отрицательным.
Знак минус перед Мс указывает на тормозящее действие момента сопротивления (усилие резания, потери трения, подъем груза, сжатие пружины и т.д.) при положительном знаке скорости.

При дальнейшем анализе уравнения движения электропривода
М –

Мс = J•dω / dt или М = Мс + J•dω / dt
нужно отметить следующее.
При спуске груза, раскручивании или разжатии пружины перед Мс ставится знак плюс, поскольку в этих случаях момент сопротивления помогает вращению привода.
Инерционный (динамический) момент J•dω / dt (правая часть уравнения) проявляется только во время переходных режимов, когда изменяется скорость.
При ускорении электропривода этот момент направлен против движения, а при торможении он поддерживает движение.
Инерционный момент как по значению, так и по знаку определяется алгебраической суммой момента двигателя и момента сопротивления.
В общем виде уравнение движения электропривода может быть записано
±М ± Мс = J•dω / dt.
Выбор знаков перед значениями моментов зависит от режима работы двигателя и характера моментов сопротивления.

В электроприводе наиболее часто

имеют место случаи, когда моменты двигателя и исполнительного механизма, а также и динамический момент ЭП являются функциями скорости. Такие переходные процессы можно условно разделить на три группы:
♦ с постоянным динамическим моментом,
♦ линейно зависящим от скорости динамическим моментом,
♦ с произвольным динамическим моментом.
Рассмотрим случай с постоянным динамическим моментом. Уравнение движения ЭП М – Мс = J•dω / dt в этом случае решается методом разделения

переменных и решение будет иметь

вид:
ω= (М – Мс)•t / J + C.
Постоянную интегрирования С можно определить из начальных условий переходного процесса.
При t = 0 ω = ωнач , тогда С = ωнач.
Окончательное решение будет иметь вид ω= (М – Мс)•t / J + ωнач.
Полученное выражение показывает, что в рассматриваемом случае скорость ω(t) линейно зависит от времени. При М – Мс > 0 скорость двигателя
увеличивается.
Время переходного процесса, за
которое скорость изменится от
начального значения до конечного
tпп = J•(ωкон - ωнач) / (М – Мс)

Рассчитать и построить зависимость скорости ω(t)

при следующих исходных данных:
Дано: М = 30 Н•м, Мс = 90 Н•м, J = 0,15 кг•м*2, ωнач = 150 рад / с.
Рассчитать время переходного процесса, за которое электропривод остановится.
Р е ш е н и е
1. Выражение для изменения скорости ЭП будет иметь вид
ω= (М – Мс)•t / J + ωнач.
2. Подставив числовые значения в приведенное выражение, получим
ω = (30 – 90)•t / 0,15 + 150 = - 400t + 150

3. Время остановки электропривода
tпп = J•(ωкон -

ωнач) / (М – Мс) = 0,15•(0 – 150) / (30 – 90) = 0,375 с.
4. Так как зависимость скорости от времени линейная, то для построения графика достаточно двух точек