Слайд 2
1.Введение.
Будем рассматривать частицы и γ - кванты
с
энергиями Е >> J =13.5 ×Z эВ. (J –
средний
потенциал ионизации атома; E < 10 МэВ).
Общая картина взаимодействия:
Слайд 3
2. Прохождение тяжелых заряженных частиц через вещество.
Частица, пролетая
сквозь вещество, «растал-кивает» атомные электроны своим кулонов-ским полем. При
этом частица теряет свою энергию – ионизационные потери, а атомы ионизуются или возбуждаются. Эти потери энергии на единицу пути будем характеризо-вать величиной - dE/dx и полным пробегом R частицы в веществе.
Слайд 4
Приближения:
- применимо классическое рассмотрение про-цесса столкновения частицы
с электроном атома – pb>> ħ;
- скорости атомных электронов
до и после столкновения малы по сравнению со скоростью налетающей частицы, или
Ечаст >> (Мчаст/me)Ee
Слайд 5
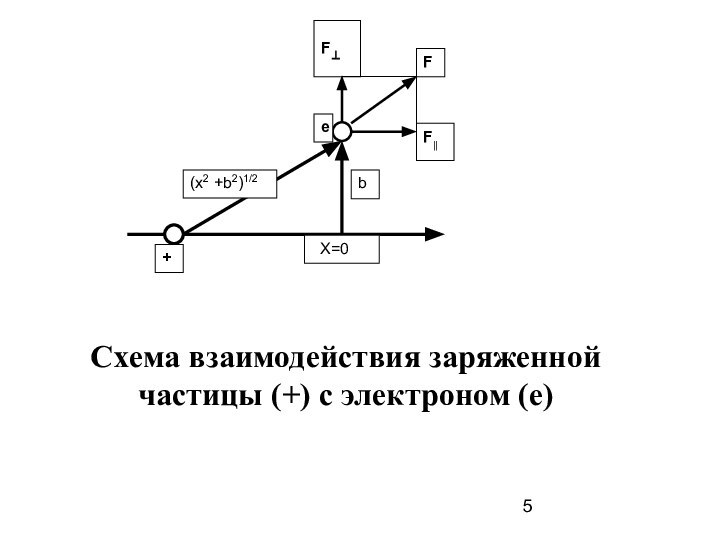
Cхема взаимодействия заряженной
частицы (+) с электроном (е)
Слайд 6
Вычислим потери энергии налетающей час-тицей при столкновении с
одним электроном.
Импульс электрона будет менятся в перпенди-кулярном направлении к
оси (Х):
Пусть взаимодействие эффективно на участке пути равном 2b, которое частица проходит за время Δt = 2b/vч. Кулоновская сила взаимодей-ствия примерно равна:
Слайд 7
Это энергия, которую теряет частица и приоб-ретает электрон
в атоме вещества.
Учтем взаимодействие со всеми электронами на рас-стоянии
b. Для этого запишем объем цилиндрического слоя радиуса b, толщиной db и высотой dx:
V = 2π ∙ b db dx. ∙ Число электронов в объеме V равно
V∙ ne=2π ∙ b∙ne db dx (ne – плотность электронов).
Слайд 8
Тогда общие потери энергии частицей:
Оценка логарифмического множителя приво-дит
к выражению для ионизационных потерь –формула Бора:
Слайд 9
Выражая скорость через энергию и массу частицы:
Выводы из
формулы Бора:
- Число ne пропорционально плотности вещества
ne =
Z ∙ ρ ∙ Na / A. Поэтому -dE/dx ~ ρ, a величина
-dE/d(ρ∙x) примерно одинакова для всех веществ.
- Величину (ρx), имеющую размерность г/см2,
принимают за единицу длины и в этих единицах
рассчитывается толщина защиты от радиации.
Слайд 10
- Зависимость -dE/dx~ 1/v2 свидетельствует, что
чем ниже
скорость частицы, тем выше потери.
Поэтому треки частиц в камере
Вильсона или в
фотоэмульсии резко утолщаются в конце пути.
- При одной и той же энергии при нерелятиви-стских скоростях потери пропорциональны массе частицы. Поэтому треки у тяжелых час-тиц жирнее и короче.
Многократно заряженные частицы сильнее
тормозятся в веществе.
Слайд 11
Формула Бора не применима при очень малых и
очень больших энергиях налетающих частиц.
Пробег R частицы в веществе
зависит от энергии, массы и заряда частицы:
Слайд 12
3. Прохождение легких заряженных частиц
через
вещество.
Механизм ионизационных потерь для электронов в общем такой же,
как и для других заряженных частиц. Отличие в малости массы электрона, что приводит к большому изменению импульса электрона в каждом столкновении, изменения первоначального направле-ния движения. С учетом всех поправок для ионизаци-онных потерь электронов получены выражения:
а –релят.:
Слайд 13
Выводы:
-При одной и той же скорости потери
примерно
одинаковы для однократно заряженных частиц
любых масс для
релятивистских энергий (например: р,е).
Слайд 14
-В нерелятивистском случае потери пропорцио-нальны массе частицы и
для протона они в 2000 раз больше чем для
электрона той же энергии.
В ультрарелятивистском пределе ионизацион-ные потери слабо зависят и от энергий и от масс частиц. Поэтому эти частицы трудно отличить по толщине треков.
Слайд 15
Заряженная частица, движущая с ускорением,
излучает электромагнитные волны.
Поэтому
электроны при столкновениях с атомами (ядра-ми) вещества излучают.
Это излучение назы-вают тормозным. Потери энергии на тормозное излучение называются радиационными. Интенсивность тормозного излучения для час-тицы с ускорением v′ в нерелятивистском нек-вантовом случае определяется соотношением:
Слайд 16
Релятивистский квантовый расчет приводит к следующей формуле для
радиационных потерь:
С увеличением энергии электронов радиационные потери становятся преобладающими
при Екр. Для оценки критической энергии получено соотношение:
Слайд 17
4. Прохождение γ - квантов через вещество.
К γ
- квантам относят электромагнитные вол-ны, длина которых, λγ ,
значительно меньше межатомных расстояний d = 10-8 см: λγ << d.
Энергия γ - квантов может принимать значение
в пределах: 10 кэВ < Еγ< 1000 ГэВ
Поскольку γ - кванты имеют нулевую массу
покоя, то скорость их должна равняться
скорости света.
Слайд 18
Поэтому, при взаимодействии с веществом
γ - кванты
или поглощаются, или рассеивают-ся на большие углы и их
интенсивность понижается: dJ = - μ J0 dx
здесь J, J0 – число частиц, проходящих через 1 см2 в 1 сек. и начальная интенсивность, соответ-ственно; μ - коэффициент поглощения;
μ /ρ - массовый коэффициент поглощения или толщина слоя вещества, измеряется в единицах г / см2.
Слайд 19
Если коэффициент поглощения разделить на
число поглощающих центров,
то получим
полное сечение рассеяния данного процесса:
μi =
niσi , а полный коэффициент поглощения
будет равен: μ=∑ μi.
Поглощение γ - квантов веществом происходит
за счет трех процессов: фотоэффекта, комптон-
эффекта и рождения электронно-позитронных
пар в кулоновском поле ядра.
Фотоэффект.
Фотоэффектом называется процесс поглощения
γ - кванта атомом с испусканием электрона.
Поскольку свободный электрон не может поглотить
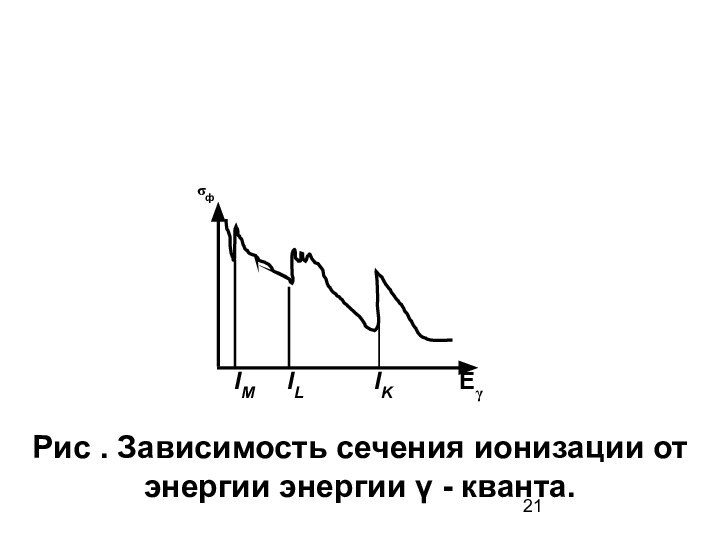
γ - квант (вследствии нарушения законов сохранения энергии и импульса), то вероятность поглощения бу-дет максимальна при Еγ ~ Есв для электронов. Таким образом, на зависимости эффективного сечения иони-зации σФ от Еγ будут наблюдаться резкие пики при Еγ равных потенциалу ионизации оболочек К, L, М и т.д.…
IM IL
IK Eγ
Рис . Зависимость сечения ионизации от энергии энергии γ - кванта.
Слайд 22
Сечение фотоионизации σф ~ Ζ5, т.е. силь-но зависит
от атомного номера вещества; растет при переходе к тяжелым
элементам; является преобладающим механизмом поглощения при низких энергиях γ-квантов: σф ≈ 6*10-16 см2 при Еγ = 1 КэВ;
σф ≈ 6*10-25 см2 при Еγ = 0.1 МэВ.
Слайд 23
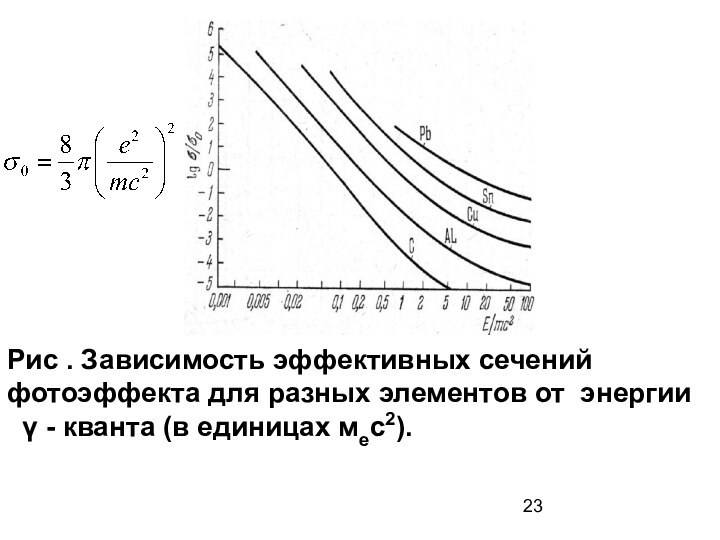
Рис . Зависимость эффективных сечений
фотоэффекта для разных
элементов от энергии
γ - кванта (в единицах мес2).
Комптон – эффект.
С увеличением
энергии γ -кванта электроны в атоме можно считать свободными и взаимодей-ствие принимает характер рассеяния. При этом наблюдается рассеянное излучение с большей длиной волны. Изменение длины волны γ - кванта равно:
Δλ = h /mec(1 - cosӨ) = Λk(1 - cosӨ),
где Θ- угол рассеяния, Λk – Комптоновская длина волны электрона:
Λk= h /mec = 2.42 ∙ 10 -10 см (0.024Å)
Слайд 25
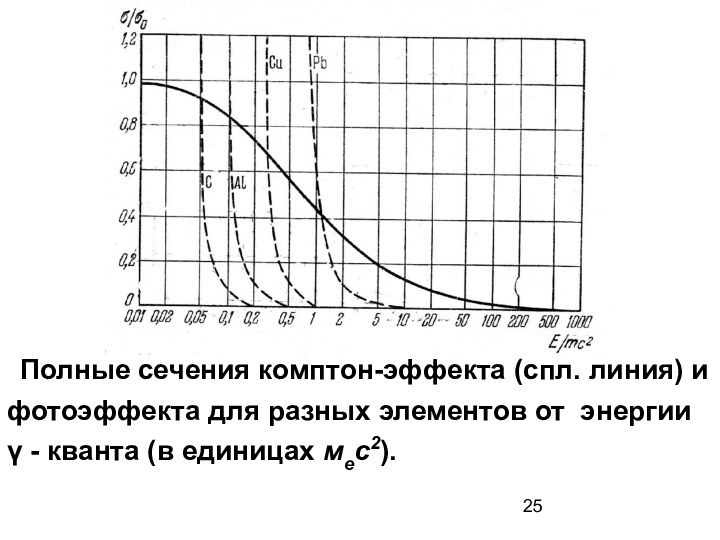
Полные сечения комптон-эффекта (спл. линия) и фотоэффекта
для разных элементов от энергии γ - кванта
(в единицах мес2).
Слайд 26
В поле ядра возможен процесс образования электрон-позитронных пар.
При высоких Еγ пороговая энергия образования равна
При образовании
электрон-позитронных пар в кулоновском поле электрона пороговая энергия γ - кванта повышается до:
Слайд 27
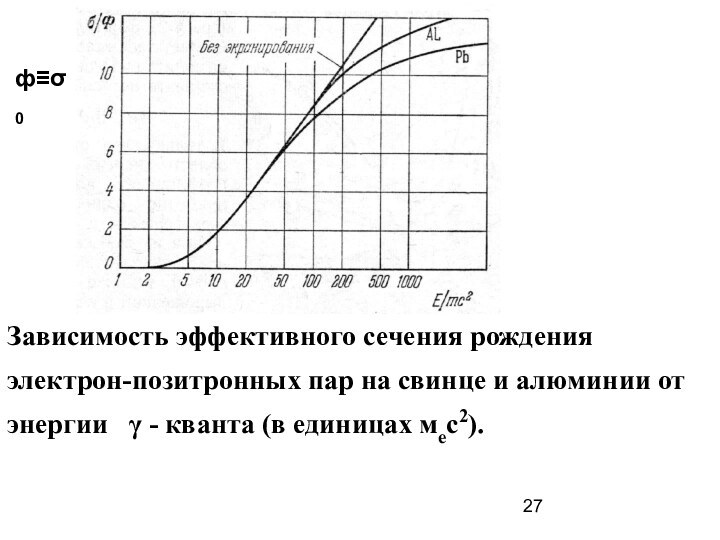
Зависимость эффективного сечения рождения электрон-позитронных пар на свинце
и алюминии от энергии γ - кванта (в
единицах мес2).
ф≡σ0
Слайд 28
В итоге, для γ - квантов, необходимо учитывать
все три процесса взаимодействия со средой: фотоэффект, эффект Комтона
и процесс образования электрон-позитронных пар:
Слайд 29
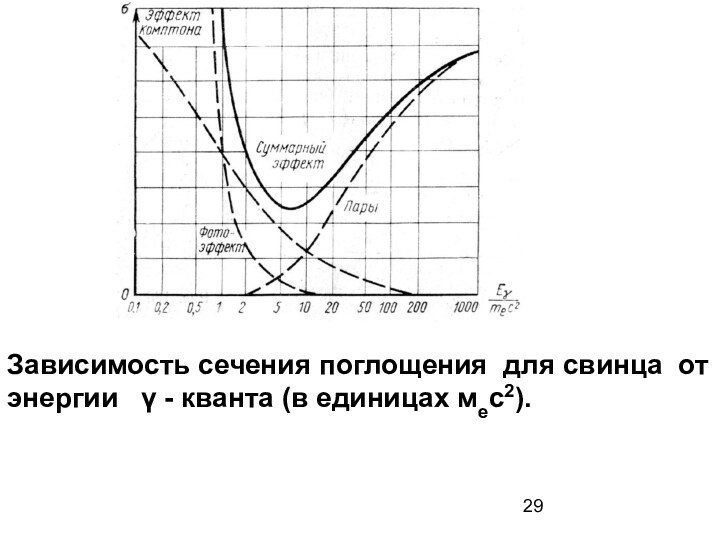
Зависимость сечения поглощения для свинца от энергии
γ - кванта (в единицах мес2).
Слайд 30
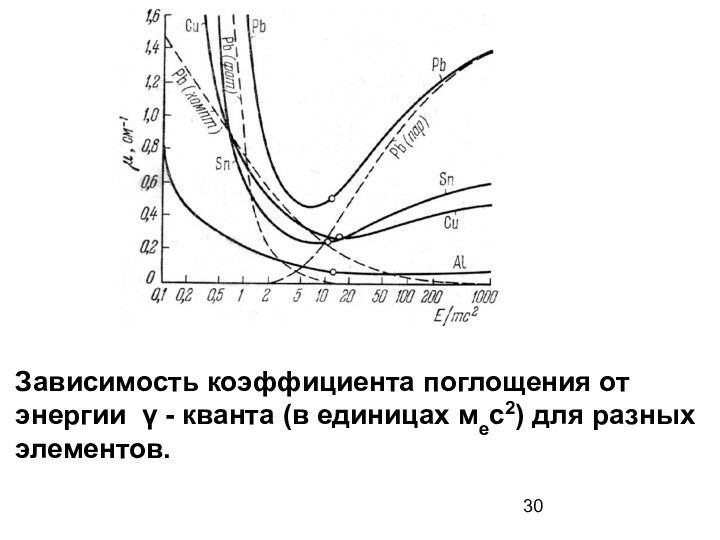
Зависимость коэффициента поглощения от энергии γ - кванта
(в единицах мес2) для разных элементов.
Слайд 31
5. Другие механизмы взаимодействия
излучения с
веществом.
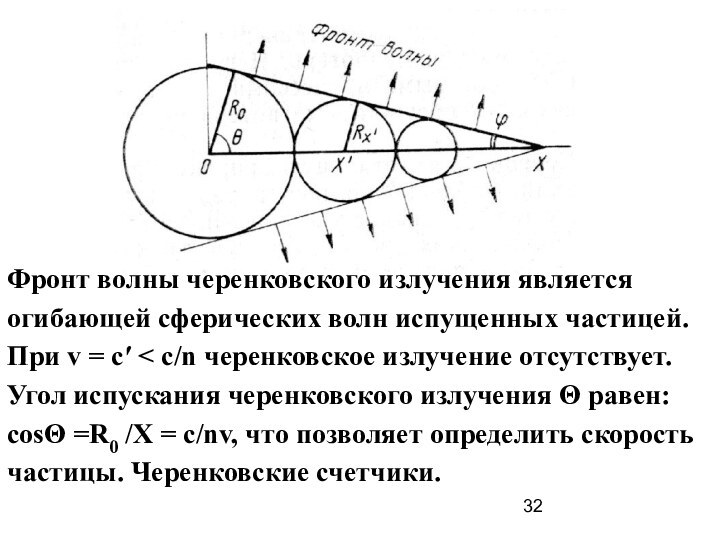
Эффект Черенкова. 1958 г. – Нобелевская пре-мия, П. Черенков,
И. Франк, И. Тамм.
Скорость света в среде определяется формулой: ν = с′ = с/n. Так как n >1, то частица может дви-гаться быстрее скорости света в среде. Такая сверхсветовая частица, если она заряжена, бу-дет излучать свет даже при неускоренном дви-жении.