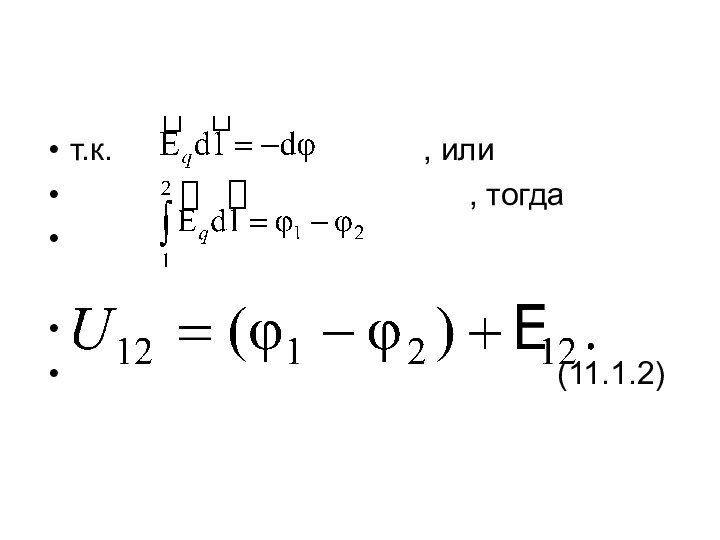Слайд 2
11.1. Закон Ома для неоднородного участка цепи
Один из основных законов электродинамики был открыт в 1822
г. немецким учителем физики Георгом Омом.
Он установил, что сила тока в проводнике пропорциональна разности потенциалов:
Слайд 3
Георг Симон Ом (1787 – 1854) – немецкий
физик.
В 1826 г. Ом открыл свой основной закон
электрической цепи. Этот закон не сразу нашел признание в науке, а лишь после того, как Э. X. Ленц, Б. С. Якоби, К. Гаусс, Г. Кирхгоф и другие ученые положили его в основу своих исследований.
Именем Ома была названа единица электрического сопротивления (Ом).
Ом вел также исследования в области акустики, оптики и кристаллооптики.
Слайд 4
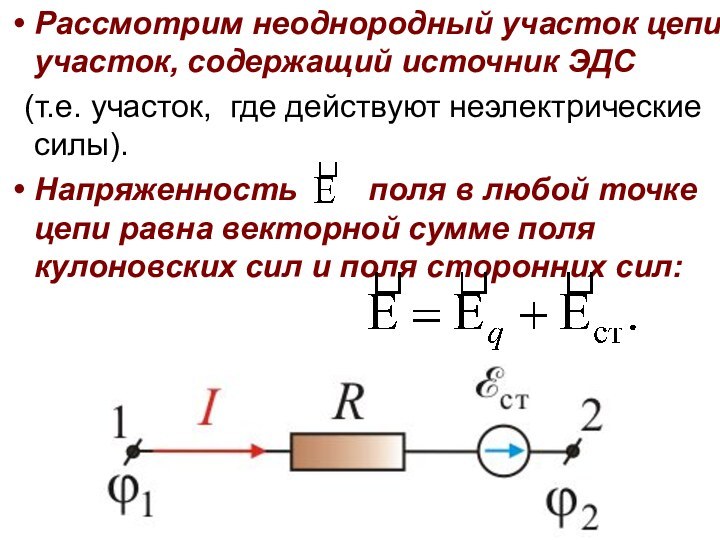
Рассмотрим неоднородный участок цепи, участок, содержащий источник ЭДС
(т.е. участок, где действуют неэлектрические силы).
Напряженность
поля в любой точке цепи равна векторной сумме поля кулоновских сил и поля сторонних сил:
Слайд 5
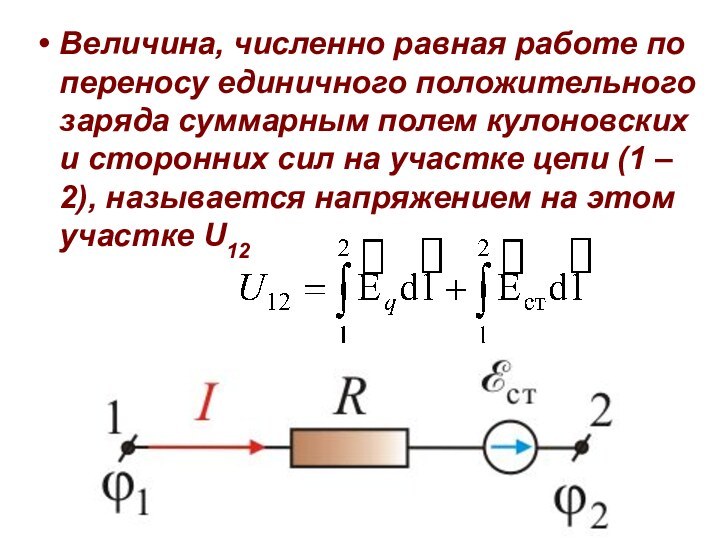
Величина, численно равная работе по переносу единичного положительного
заряда суммарным полем кулоновских и сторонних сил на участке
цепи (1 – 2), называется напряжением на этом участке U12
Слайд 7
Напряжение на концах участка цепи совпадает с разностью
потенциалов только в случае, если на этом участке нет
ЭДС, т.е. на однородном участке цепи.
Запишем обобщенный закон Ома для участка цепи содержащей источник ЭДС:
(11.1.3)
Слайд 8
Обобщенный закон Ома выражает закон сохранения энергии применительно
к участку цепи постоянного тока.
Он в равной мере
справедлив как для пассивных участков (не содержащих ЭДС), так и для активных.
Слайд 9
В электротехнике часто используют термин падение напряжения –
изменение напряжения вследствие переноса заряда через сопротивление
Слайд 10
В замкнутой цепи:
;
или где ; r – внутреннее сопротивление активного участка цепи
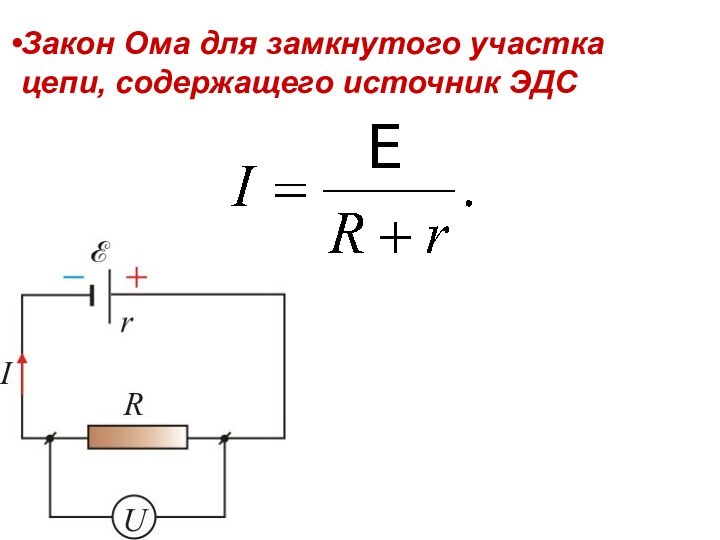
Тогда закон Ома для замкнутого участка цепи, содержащего источник ЭДС запишется в виде
(11.1.1)
Слайд 11
Закон Ома для замкнутого участка цепи, содержащего источник
ЭДС
Слайд 12
11.2. Закон Ома в дифференциальной форме
Закон Ома в
интегральной форме для однородного участка цепи (не содержащего ЭДС)
(11.2.1)
Для однородного линейного проводника выразим R через ρ:
(11.2.2)
ρ – удельное объемное сопротивление; [ρ] = [Ом·м].
Слайд 13
Найдем связь между и
в бесконечно малом объеме проводника – закон Ома в
дифференциальной форме.
Слайд 14
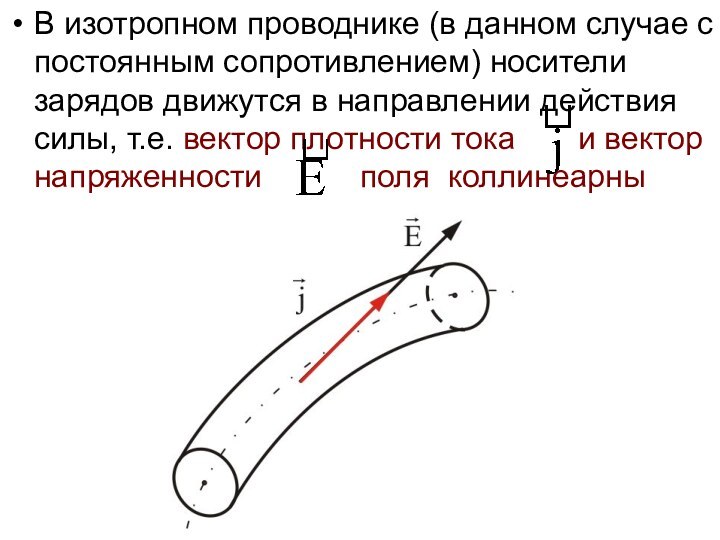
В изотропном проводнике (в данном случае с постоянным
сопротивлением) носители зарядов движутся в направлении действия силы, т.е.
вектор плотности тока и вектор напряженности поля коллинеарны
Слайд 15
Исходя из закона Ома (11.2.1), имеем:
А мы знаем,
что
. Отсюда
можно записать
(11.2.3)
это запись закона Ома в дифференциальной форме.
Здесь – удельная электропроводность.
Слайд 16
Плотность тока можно выразить через заряд электрона е,
количество зарядов n и дрейфовую скорость :
Обозначим
, тогда ;
(11.2.4)
Слайд 17
Теперь, если удельную электропроводность σ выразить через е,
n и b:
то вновь получим выражение закона Ома в дифференциальной форме:
Слайд 18
11.3. Работа и мощность тока. Закон Джоуля –
Ленца
Рассмотрим произвольный участок цепи, к концам которого приложено напряжение
U. За время dt через каждое сечение проводника проходит заряд
При этом силы электрического поля, действующего на данном участке, совершают работу:
Общая работа:
Слайд 19
Разделив работу на время, получим выражение для мощности:
(11.3.1)
Полезно вспомнить и другие формулы для мощности и работы:
(11.3.2)
(11.3.3)
В 1841 г. манчестерский пивовар Джеймс Джоуль и в 1843 г. петербургский академик Эмилий Ленц установили закон теплового действия электрического тока.
Слайд 20
Джоуль Джеймс Пресскотт (1818 – 1889) – английский
физик, один из первооткрывателей закона сохранения энергии. Первые уроки
по физике ему давал Дж. Дальтон, под влиянием которого Джоуль начал свои эксперименты. Работы посвящены электромагнетизму, кинетической теории газов.
Ленц Эмилий Христианович (1804 – 1865) – русский физик. Основные работы в области электромагнетизма. В 1833 г. установил правило определения электродвижущей силы индукции (закон Ленца), а в 1842 г. (независимо от Дж. Джоуля) – закон теплового действия электрического тока (закон Джоуля-Ленца). Открыл обратимость электрических машин. Изучал зависимость сопротивление металлов от температуры. Работы относятся также к геофизике.
Слайд 21
При протекании тока, в проводнике выделяется количество теплоты:
(11.3.4)
Если ток изменяется со временем:
Это закон Джоуля – Ленца в интегральной форме.
Слайд 22
Отсюда видно, что нагревание происходит за счет работы,
совершаемой силами поля над зарядом.
Соотношение (11.3.4) имеет интегральный характер
и относится ко всему проводнику с сопротивлением R, по которому течет ток I.
Получим закон Джоуля-Ленца в локальной - дифференциальной форме, характеризуя тепловыделение в произвольной точке.
Слайд 23
Тепловая мощность тока в элементе проводника Δl, сечением
ΔS, объемом
равна:
Удельная мощность тока
Слайд 24
Согласно закону Ома в дифференциальной форме
, получим
закон Джоуля - Ленца в дифференциальной форме, характеризующий плотность выделенной энергии.
Так как выделенная теплота равна работе сил электрического поля
то мы можем записать для мощности тока:
(11.3.2)
Слайд 25
Мощность, выделенная в единице объема проводника .
Приведенные формулы
справедливы для однородного участка цепи и для неоднородного.
Слайд 26
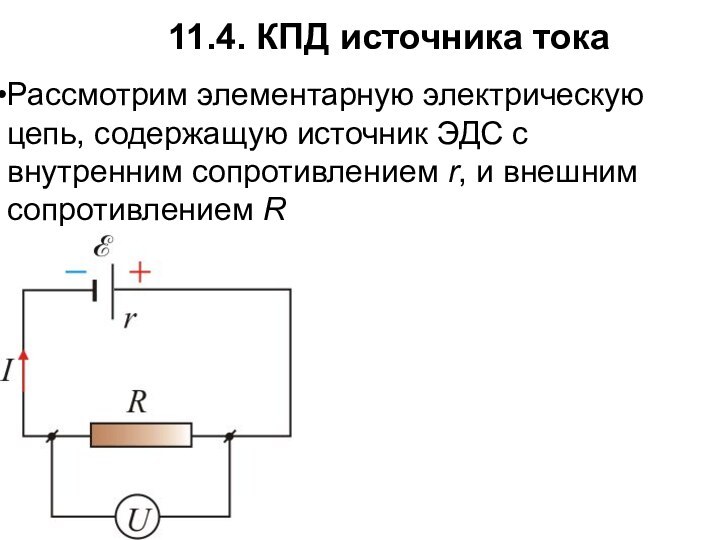
11.4. КПД источника тока
Рассмотрим элементарную электрическую цепь, содержащую
источник ЭДС с внутренним сопротивлением r, и внешним сопротивлением
R
Слайд 27
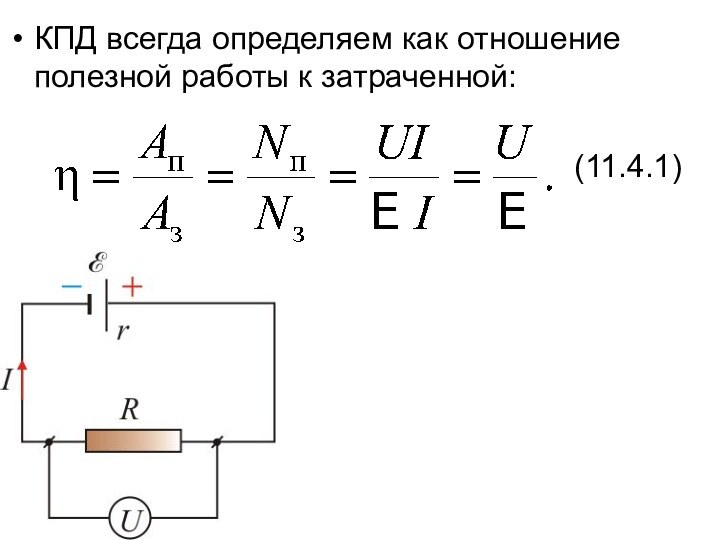
КПД всегда определяем как отношение полезной работы к
затраченной:
(11.4.1)
Слайд 28
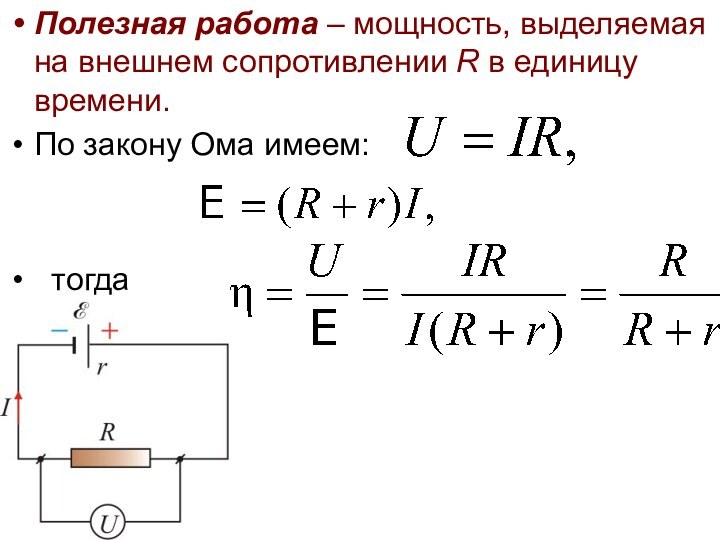
Полезная работа – мощность, выделяемая на внешнем сопротивлении
R в единицу времени.
По закону Ома имеем:
тогда
Слайд 29
Таким образом, имеем, что при
но при этом
ток в цепи мал и полезная мощность мала.
Вот парадокс – мы всегда стремимся к повышенному КПД, а в данном случае нам это не приносит пользы.
Найдем условия, при которых полезная мощность будет максимальна.
Для этого нужно, чтобы
Слайд 31
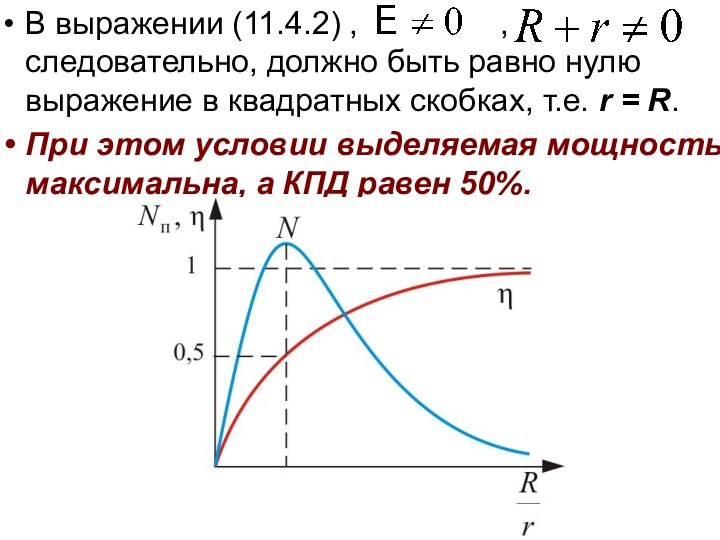
В выражении (11.4.2) ,
, следовательно, должно быть равно нулю
выражение в квадратных скобках, т.е. r = R.
При этом условии выделяемая мощность максимальна, а КПД равен 50%.
Слайд 32
11.5. Правила Кирхгофа для разветвленных цепей
Расчет разветвленных цепей
с помощью закона Ома довольно сложен.
Эта задача решается
более просто с помощью двух правил немецкого физика Г. Кирхгофа (1424 – 1443).
Слайд 33
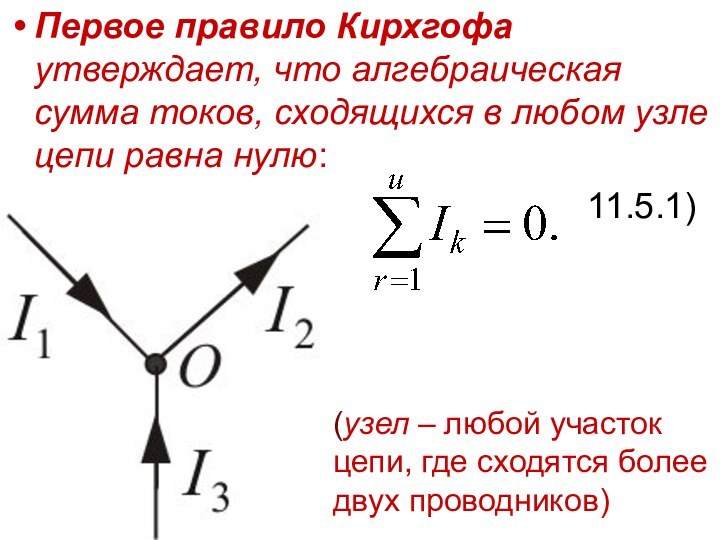
Первое правило Кирхгофа утверждает, что алгебраическая сумма токов,
сходящихся в любом узле цепи равна нулю:
11.5.1)
(узел – любой участок цепи, где сходятся более двух проводников)
Слайд 34
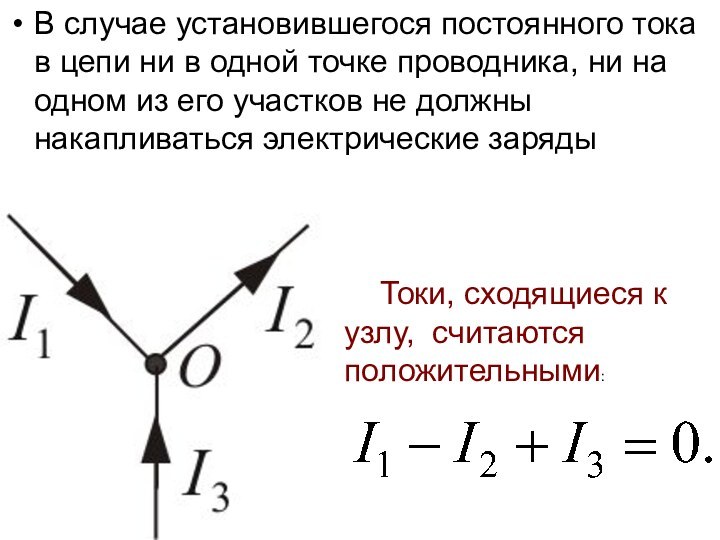
В случае установившегося постоянного тока в цепи ни
в одной точке проводника, ни на одном из его
участков не должны накапливаться электрические заряды
Токи, сходящиеся к узлу, считаются положительными:
Слайд 35
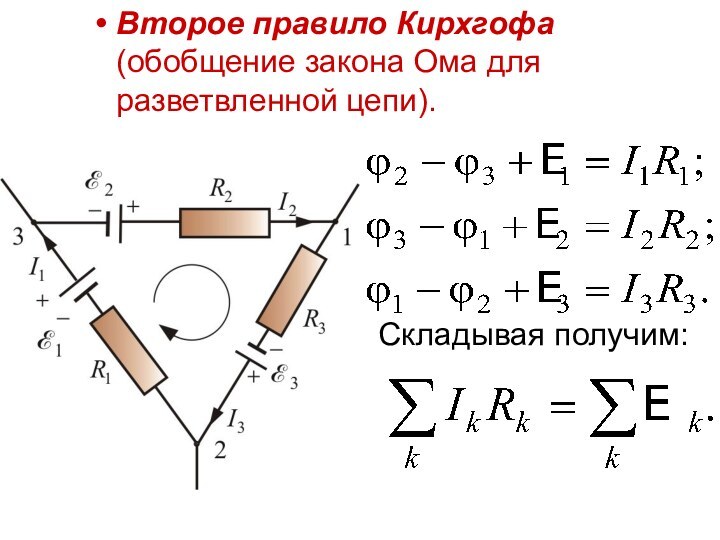
Второе правило Кирхгофа (обобщение закона Ома для разветвленной
цепи).
Складывая получим:
Слайд 36
В любом замкнутом контуре электрической цепи алгебраическая сумма
произведения тока на сопротивление равна алгебраической сумме ЭДС, действующих
в этом же контуре.
Обход контуров осуществляется по часовой стрелке, если направление обхода совпадает с направлением тока, то ток берется со знаком «плюс».