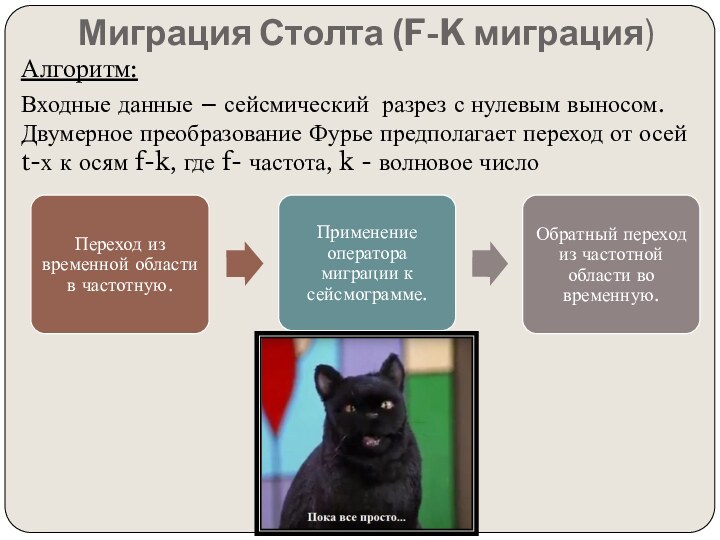
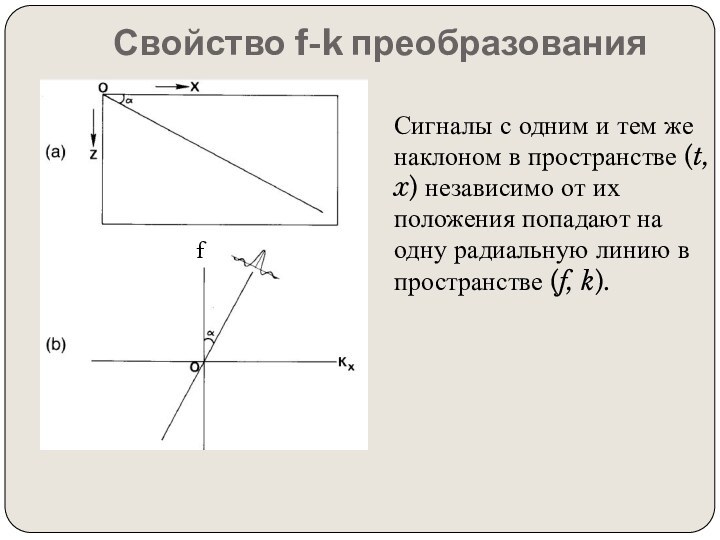
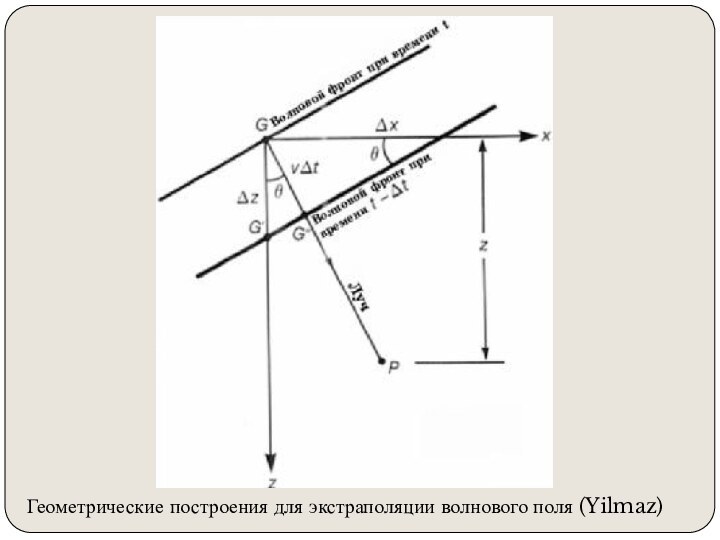
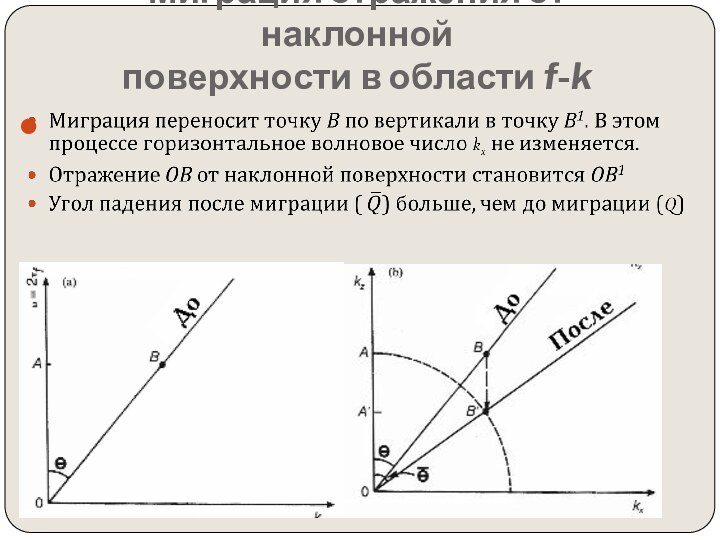
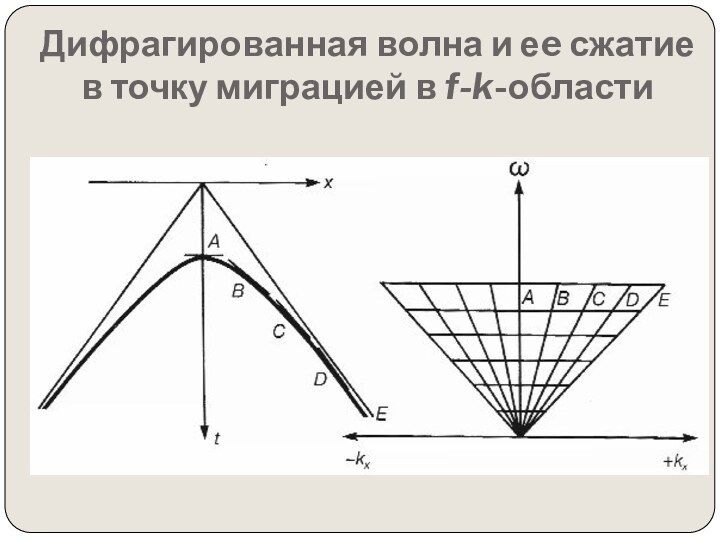
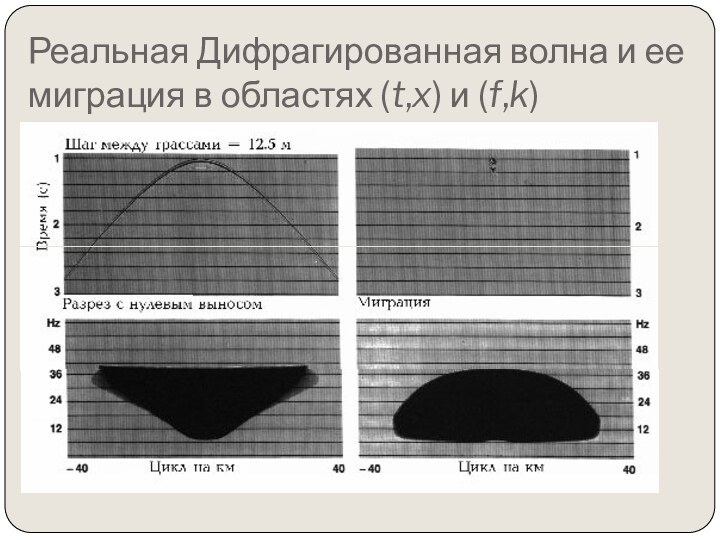
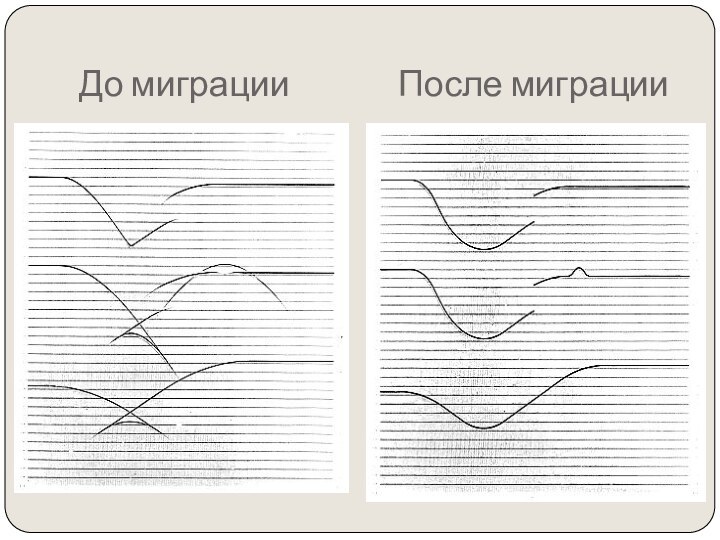
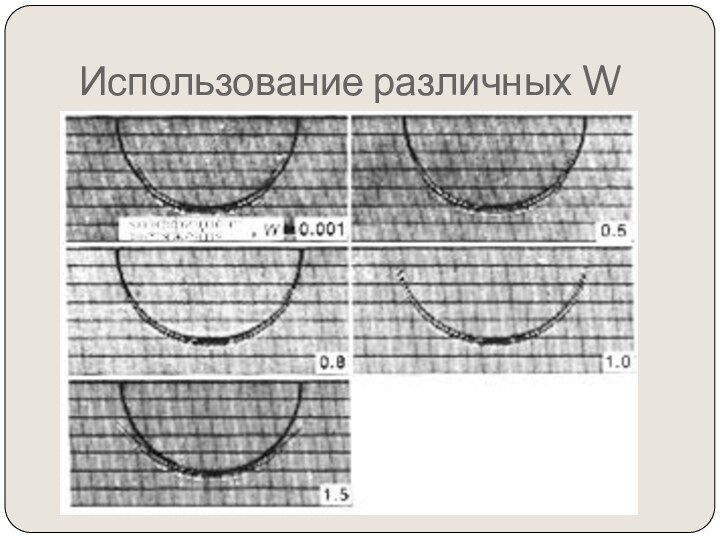
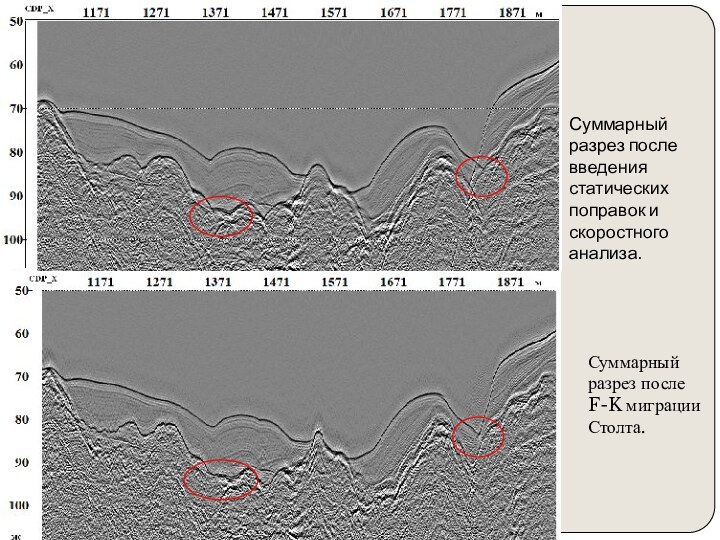
том, чтобы итоговый мигрированнный сейсмический разрез выглядел так же,
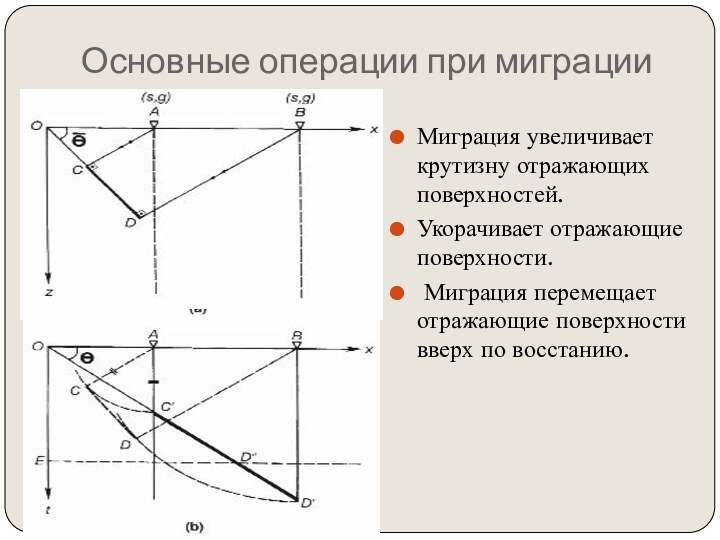
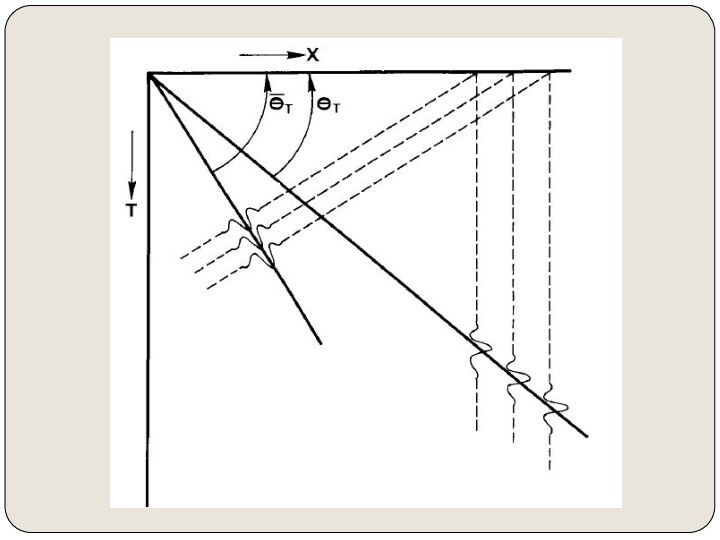
как геологический разрез по профилю сьемки.Миграция перемещает наклонные отражающие поверхности в их истинные положения в разрезе и сжимает дифрагированные волны, тем самым подчеркивая элементы разреза (разломы, внедрения и т.д.)
(Yilmaz, seismic data processing)