Слайд 2
1. Прямая геодезическая угловая засечка (ПГУЗ)
ПГУЗ применяется для
определения координат дополнительной точки на основании двух исходных пунктов
с известными координатами. Для обеспечения надежного контроля измерений и повышения точности определения положения искомого пункта на практике, как правило, применяют многократные прямые засечки не менее чем с трех исходных пунктов.
Вычисление координат определяемой точки в зависимости от условий наблюдений может быть выполнено по формулам Юнга либо по формулам Гаусса.
Слайд 3
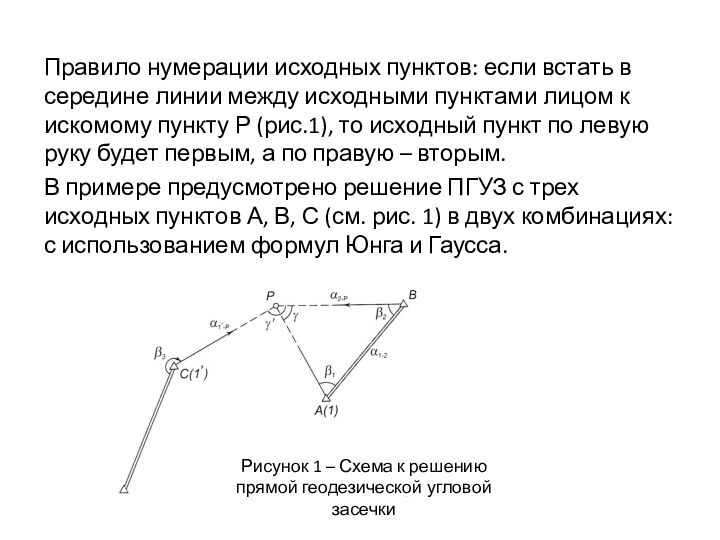
Правило нумерации исходных пунктов: если встать в середине
линии между исходными пунктами лицом к искомому пункту Р
(рис.1), то исходный пункт по левую руку будет первым, а по правую – вторым.
В примере предусмотрено решение ПГУЗ с трех исходных пунктов А, В, С (см. рис. 1) в двух комбинациях: с использованием формул Юнга и Гаусса.
Рисунок 1 – Схема к решению
прямой геодезической угловой засечки
Слайд 4
1 вариант: Решение ПГУЗ по измеренным углам –
если между двумя исходными пунктами А и В имеется
взаимная видимость, то решение задачи выполняют по формулам Юнга:
(1)
Слайд 5
2 вариант. Решение ПГУЗ по дирекционным углам направлений
– если между исходным пунктами А и С (рис.1)
отсутствует взаимная видимость, то для решения используются формулы Гаусса.
либо
(2)
(3)
Слайд 6
Оценка точности прямой геодезической засечки. Среднюю квадратическую погрешность
положения искомого пункта Р, определенного по двум исходным пунктам,
находят по формуле:
где
средняя квадратическая погрешность измерения угла;
γ – угол при определяемой точке Р; ρ = 206265ʹʹ; d1 и d2 – расстояния от исходных пунктов до точки Р.
Расхождения в значениях абсцисс и ординат определяемого пункта Р, полученные из решения по двум комбинациям, должны удовлетворять условию:
r ≤ 3M
(4)
(5)
Слайд 7
Формулы Юнга и Гаусса для решения ПГУЗ находят
широкое применение при решении как отдельных треугольников, так и
различных систем цепей треугольников, геодезических четырехугольников, центральных систем и т.п.
Недостатком пользования этими формулами является то, что они не дают возможности определять расстояние между пунктами; значения последних при оценке точности приходится определять решением обратной геодезической задачи.
Слайд 8
2. Обратная геодезическая угловая засечка (ОГУЗ) (задача Потенота)
Сущность
ОГУЗ состоит в определении координат дополнительной точки Р путем
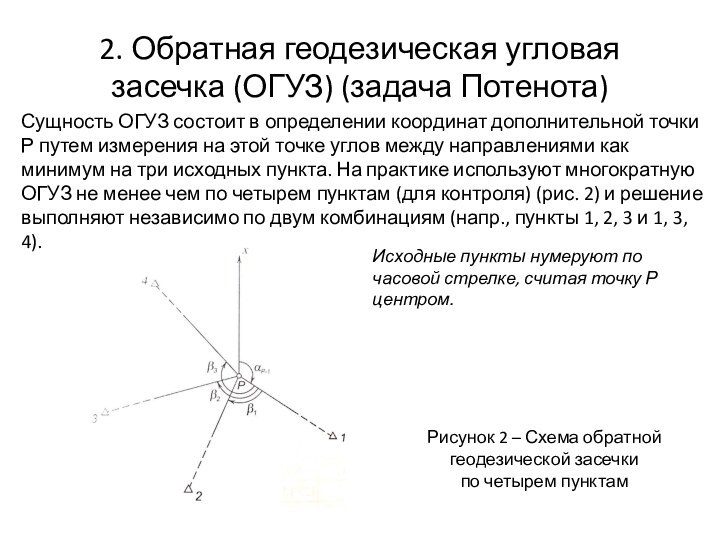
измерения на этой точке углов между направлениями как минимум на три исходных пункта. На практике используют многократную ОГУЗ не менее чем по четырем пунктам (для контроля) (рис. 2) и решение выполняют независимо по двум комбинациям (напр., пункты 1, 2, 3 и 1, 3, 4).
Рисунок 2 – Схема обратной геодезической засечки
по четырем пунктам
Исходные пункты нумеруют по часовой стрелке, считая точку Р центром.
Слайд 9
Решение задачи выполняют способом Деламбра в следующей последовательности:
1.
Вычисляют дирекционный угол направления с исходного пункта 1 на
определяемую точку Р по формуле:
2. Определяют дирекционные углы направлений с других исходных пунктов (2, 3, 4):
α2-Р = α1-Р + β1; α3-Р = α1-Р + β2; α4-Р = α1-Р + β3.
3. Используя формулы Гаусса (2) или (3), вычисляют координаты точки Р в двух комбинациях.
(6)
Слайд 10
Оценка точности ОГУЗ. СКП определения положения точки Р
находят по формуле:
где
средняя квадратическая погрешность измерения угла;
ρ
= 206265ʹʹ. Остальные буквенные обозначения угловых и линейных величин приведены на схеме рис. 3 (в скобках – обозначения величин для II комбинации пунктов 2, 3, 4).
(7)
Рисунок 3 – Схема к оценке точности обратной геодезической угловой засечки
Слайд 11
Общая СКП определения положения пункта Р:
(8)
Расхождения в значениях
координат определяемого пункта Р, полученные из решения по двум
комбинациям, должны удовлетворять условию (5).
Слайд 12
3. Комбинированная геодезическая засечка (КГЗ)
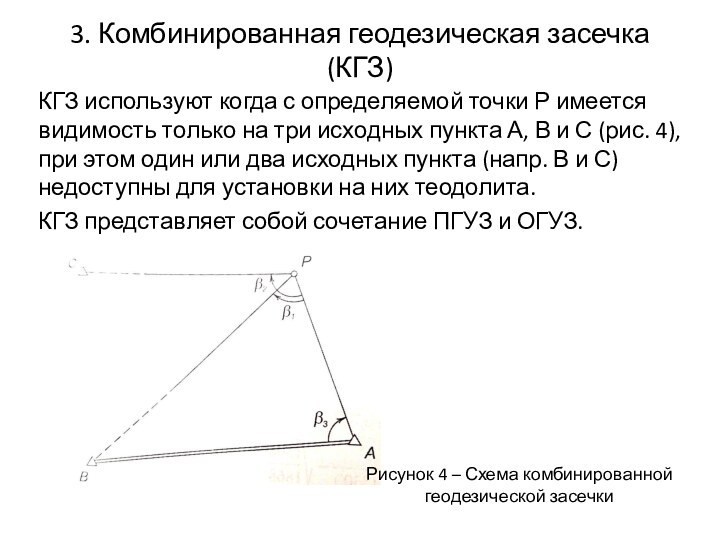
КГЗ используют когда с
определяемой точки Р имеется видимость только на три исходных
пункта А, В и С (рис. 4), при этом один или два исходных пункта (напр. В и С) недоступны для установки на них теодолита.
КГЗ представляет собой сочетание ПГУЗ и ОГУЗ.
Рисунок 4 – Схема комбинированной геодезической засечки
Слайд 13
Порядок решения:
По измеренным углам β1, β2 и координатам
исходных пунктов А, В и С решением ОГУЗ находят
координаты точки Р.
По координатам исходных пунктов А и В решением обратной геодезической задачи определяют дирекционный угол стороны АВ.
По дирекционному углу αАВ и измеренным углам β1, β2, β3 вычисляют дирекционные углы направлений с исходных пунктов на точку Р – αАР, αВР, αСР.
Решением ПГУЗ по формулам Гаусса находят координаты точки Р.
Слайд 14
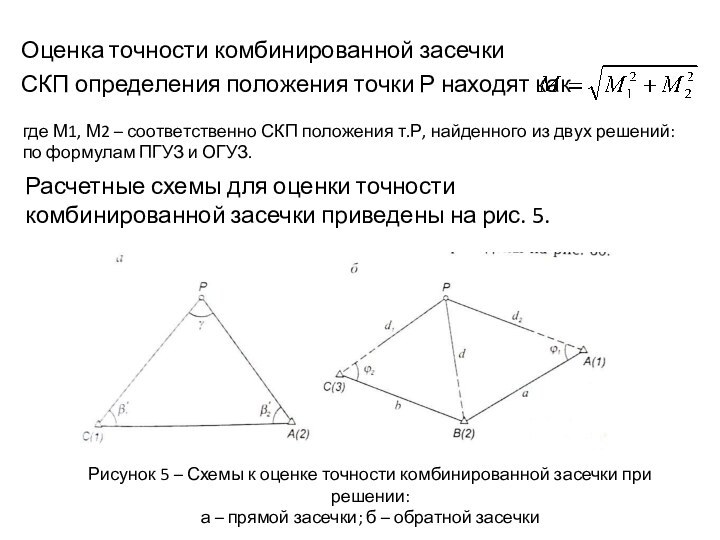
Расчетные схемы для оценки точности комбинированной засечки приведены
на рис. 5.
где М1, М2 – соответственно СКП положения
т.Р, найденного из двух решений: по формулам ПГУЗ и ОГУЗ.
Оценка точности комбинированной засечки
СКП определения положения точки Р находят как
Рисунок 5 – Схемы к оценке точности комбинированной засечки при решении:
а – прямой засечки; б – обратной засечки
Слайд 15
Для прямой засечки с исходных пунктов С и
А (см. рис. 5а):
Для обратной засечки на исходные пункты
А. В, С (см. рис. 5б):
Расхождение между координатами точки Р, найденными из двух решений должно удовлетворять условию:
Слайд 16
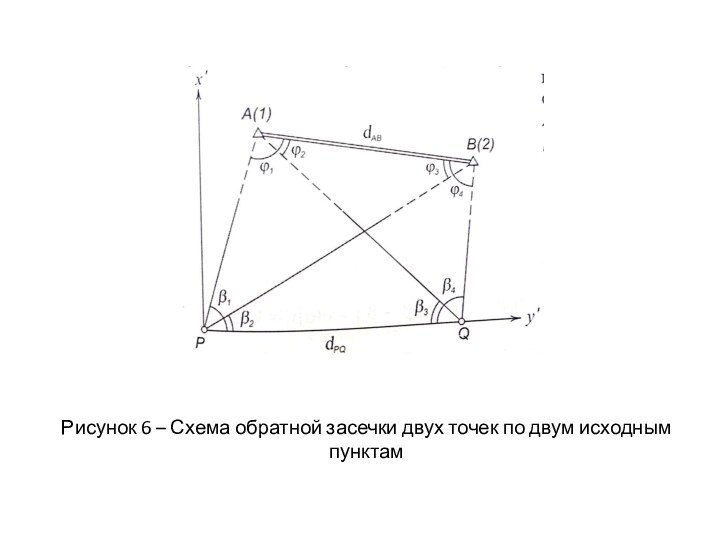
4. Определение обратной засечкой двух точек по двум
исходным пунктам (задача Ганзена)
Данный способ позволяет определить положение двух
дополнительных точек Р и Q при наличии видимости с каждой из них на два исходных пункта А и В и взаимной видимости между ними (рис. 6).
Такая задача возникает при сгущении городских спутниковых сетей, когда невозможно установить спутниковый приемник на центрах пунктов, закрепленных стенными знаками, либо при наличии вблизи пунктов экранирующих препятствий и отражающих поверхностей. В таких случаях спутниковый приемник устанавливают над вспомогательным рабочим центром.
На определяемых точках Р и Q измеряют углы β1, β2, β3 и β4, образованные направлениями на исходные пункты А и В и соответственно на точки Q и Р (см. рис. 6).
Слайд 17
Рисунок 6 – Схема обратной засечки двух точек
по двум исходным пунктам
Слайд 18
Порядок решения
1. Для определения вспомогательных углов ϕ1, ϕ2,
ϕ3, и ϕ4 вводят условную систему координат (см. рис.6):
т.Р принимают за начало условных координат хʹ, уʹ, направление PQ – за положительное направление оси ординат; длину стороны PQ условно принимают равной 1000,00м. Тогда условные координаты точек P и Q будут:
хʹР = 0; уʹР = 0; хʹQ = 0; уʹQ = 1000,00м.
2. Из треугольников PAQ и PBQ по формулам Юнга находят условные координаты точек А и В.
3. Решением обратной геодезической задачи по исходным координатам пунктов А и В определяют условный дирекционный угол.
4. Вычисляют дирекционные углы направлений с исходных пунктов на определяемые точки, учитывая, что условный дирекционный угол направления PQ равен 90°.
Слайд 19
5. Используя полученные условные дир. углы, вычисляют вспомогательные
углы ϕ1, ϕ2, ϕ3, и ϕ4.
6. Из треугольников АВР
и АВQ, используя вспомогательные углы ϕ1, ϕ2, ϕ3, и ϕ4 , по формулам Юнга вычисляют координаты определяемых точек Р и Q.
Контролем правильности измерений и вычислений является сравнение длины стороны РQ, вычисленной по координатам с непосредственно измеренной длиной.
Слайд 20
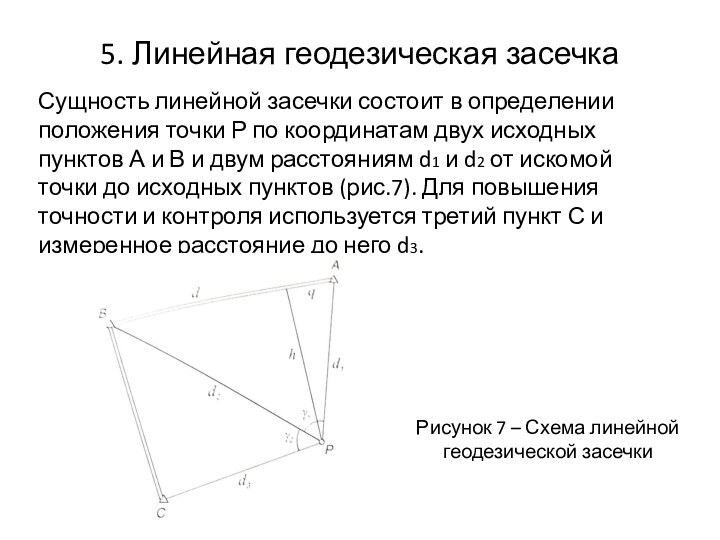
5. Линейная геодезическая засечка
Сущность линейной засечки состоит в
определении положения точки Р по координатам двух исходных пунктов
А и В и двум расстояниям d1 и d2 от искомой точки до исходных пунктов (рис.7). Для повышения точности и контроля используется третий пункт С и измеренное расстояние до него d3.
Рисунок 7 – Схема линейной геодезической засечки
Слайд 21
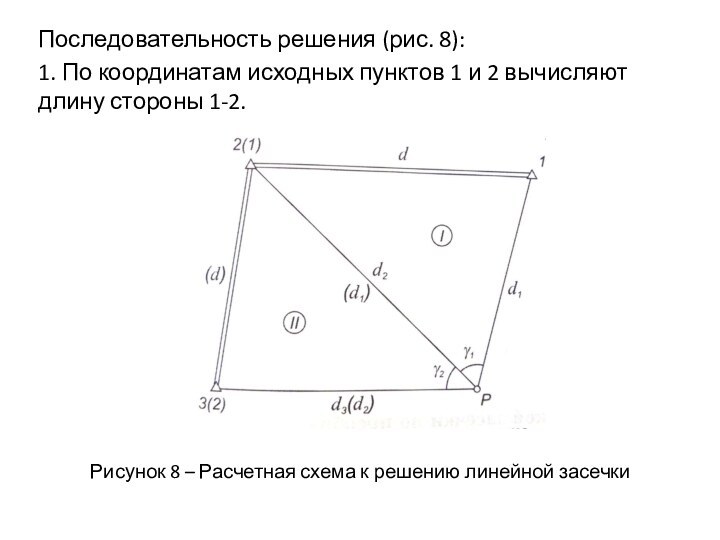
Последовательность решения (рис. 8):
1. По координатам исходных пунктов
1 и 2 вычисляют длину стороны 1-2.
Рисунок 8 –
Расчетная схема к решению линейной засечки
Слайд 22
2. По длинам сторон рассчитывают вспомогательные величины:
В последнем
выражении знак «+» или «-» выбирают соответственно направлению следования
вершин 1, Р, 2 (по ходу или против хода часовой стрелки).
3. Вычисляют приращения координат:
Δх = qʹ(х2 – х1) + hʹ(y2 – y1),
Δy = qʹ(y2 – y1) – hʹ(х2 – х1),
и координаты искомого пункта Р:
хР = х1 + Δх,
уР = у1 + Δу.
Слайд 23
Контроль можно выполнить двумя способами:
Путем сравнения длины стороны
3-Р, вычисленной по координатам, с измеренной длиной d3;
Сравнением значений
координат точки Р, полученных из решения двух треугольников (в двух комбинациях).
Слайд 24
Оценка точности линейной геодезической засечки
СКП положения искомого пункта
Р находят по формулам:
Слайд 25
6. Лучевой (полярный) метод
Лучевой метод, разработанный профю Ю.Г.
Батраковым, основан на использовании электромагнитных дальномеров (эл. тахеометров). Его
удобно применять в открытой холмистой местности при ограниченном числе пунктов опорной геодезической сети, когда непосредственно с центра пункта имеется видимость по многим направлениям.
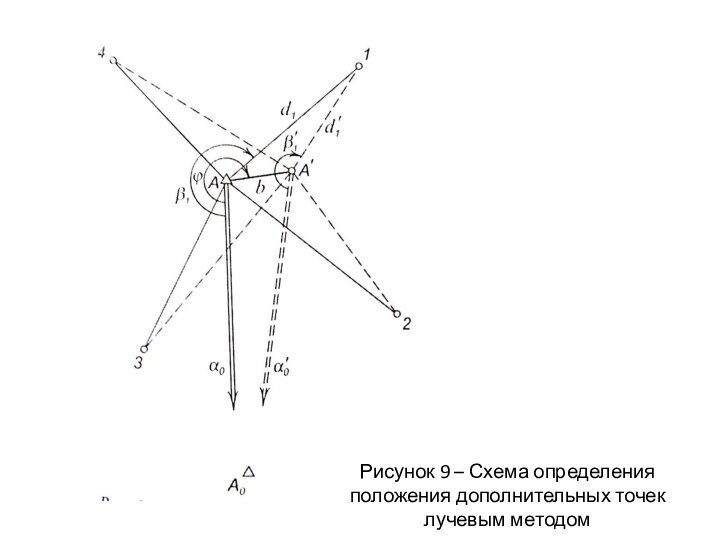
Сущность метода заключается (рис. 9) в определении положения точек полярным методом с двух пунктов: основного А и дополнительного Аʹ.
Слайд 26
Рисунок 9 – Схема определения положения дополнительных точек
лучевым методом
Слайд 27
Решение задачи складывается из двух этапов:
Определение координат дополнительного
пункта Аʹ и дирекционных углов исходных направлений (см. рис.
9).
По полярным координатам d, β дважды (относительно пунктов А и Аʹ) вычисляют координаты искомых точек 1, 2, 3, 4.