Презентация на тему по информатике Рекурсия

является суммой двух предыдущих. Это числа Фибоначчи. Формальное их

определение таково:
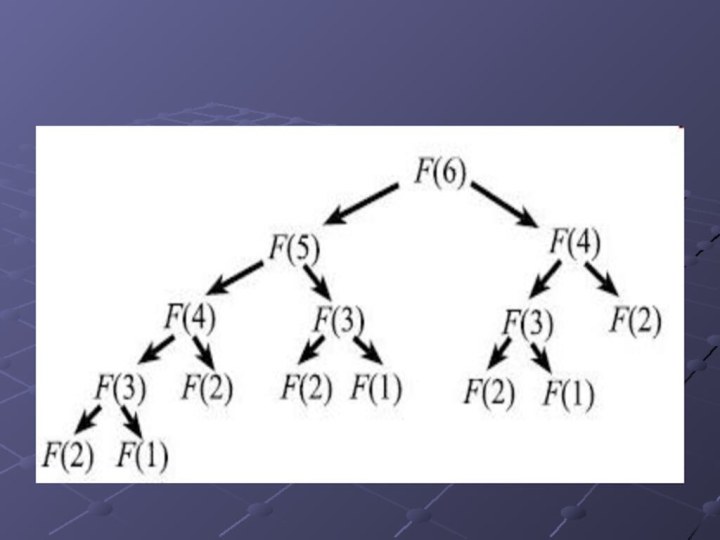
F(1) = 1, F(2) = 1, F(n) = F(n − 2) + F(n − 1), если n > 2.

Функция F(n) задана рекурсивно, то есть «через себя». База — значения функции F на аргументах 1 и 2, а шаг —
формула F(n) = F(n − 2) + F(n − 1).

Современные языки программирования дают возможность программировать рекурсивные определения без особых усилий, но в таких определениях таятся опасности.

рассмотреть вычисление F(n) при больших n, то повторных вычислений

будет очень много. Это и есть основной недостаток рекурсии — повторные вычисления одних и тех же значений. Кроме того, с рекурсивными функциями связана одна серьезная ошибка: дерево рекурсивных вызовов может оказаться бесконечным и компьютер «зависнет». Важно, чтобы процесс сведения задачи к более простым когда-нибудь заканчивался.

Есть способ решить проблему повторных вычислений. Он очевиден — нужно запоминать найденные значения, чтобы не вычислять их каждый раз заново. Конечно, для этого придётся активно использовать память.

тремя «строчками»:
создать глобальный массив FD, состоящий из нулей;
после вычисления

числа Фибоначчи F(n) поместить его значение в FD[n];
в начале рекурсивной процедуры сделать проверку на то, что FD[n] = 0 и, если , то вернуть FD[n] в качестве результата, а иначе приступить к рекурсивному вычислению F(n).

Такая рекурсия с запоминанием называется динамическим программированием сверху.

Для чисел Фибоначчи есть простой «человеческий алгоритм», не использующий рекурсивные вызовы и запоминание всех вычисленных значений. Достаточно помнить два последних числа Фибоначчи, чтобы вычислить следующее. Затем предпредыдущее можно «забыть» и перейти к вычислению следующего:
a = b = 1;
если n > 2, то сделать n − 2 раз: c = a + b; a = b; b = c;
вернуть ответ b;

Этот алгоритм линейный по n, то есть для вычисления n-го числа Фибоначчи требуется n шагов. Но здесь есть важная тонкость: число знаков в числе Фибоначчи растёт с n, соответственно, время выполнения операции сложения c = a + b тоже увеличивается.

примерно линейно (в любой системе счисления). Это следует из

явной формулы:

точности (на компьютерах с 32-битной архитектурой это означает «меньше

232»), сложение выполняется за фиксированное число тактов. Но, начиная с F(48), уже нельзя использовать элементарные 32-битные целочисленные типы и нужно использовать 64-битные или писать «свою» длинную арифметику, то есть представлять числа в виде массивов цифр в некоторой системе счисления (обычно используют систему с основанием 10000) и писать процедуры сложения таких чисел «столбиком». Например, число десятичных знаков в 1000-м числе Фибоначчи равно 209, и для сложения F(1001) = F(1000) + F(999) «столбиком» в десятичной системе счисления потребуется примерно 209 элементарных операций. Определение сложности задачи вычисления F(n) при больших n довольно трудная задача.

рекурсивные алгоритмы — игру «Ханойские башни», придуманную ещё в

1883 году Эдуардом Люка. Есть три стержня и 64 кольца́, нанизанных на них. В начале все ко́льца находятся на первом стержне, причём все ко́льца разного диаметра, и меньшие ко́льца лежат на бо́льших. За ход разрешается взять верхнее кольцо с любого стержня и положить на другой стержень сверху, при этом запрещается класть большее кольцо на меньшее. Цель игры состоит в том, чтобы переместить всю пирамиду с первого стержня на второй.


Заметим, что для того, чтобы переместить пирамиду, нам надо будет переместить и самое нижнее большое кольцо. Для этого нам нужно будет, чтобы все остальные ко́льца были на третьем штыре. Значит, чтобы переместить N колец, нам сначала нужно переместить столбик из верхних N − 1 колец на третий стержень, затем переместить самое большое кольцо с первого на второй и, наконец, переместить столбик из N − 1 колец с третьего стержня на второй.

Move(n:integer; x,y,z:char);
{x-первая башня; y-вторая башня; z-третья башня}
Begin
if n>=1

then begin
Move(n-1,x,z,y) {шаг 1}
write(x,’->’,z,’ ‘); {шаг 2}
inc(i);
if i mod 8 =0 then writeln;
move(n-1,y,x,z);
end;

Тело рекурсивной подпрограммы

Фибоначчи, конечно же, достаточно примитивен и очень распространен, но

почему-то такие ошибки встречаются сплошь и рядом. Очень просто заставить рекурсию десять раз вычислять одно и то же...

Тем не менее, бывают случаи, когда переход к рекурсии от хорошего итеративного алгоритма будет давать преимущества, несмотря на то, что реализованы одинаково. Это алгоритмы, в которых используется стек.

Вообще говоря, стек и рекурсия взаимозаменяемы. То есть, все что можно сделать при помощи рекурсии, можно заменить на "условно бесконечный" цикл с использованием стека и наоборот. Это очень часто используется тогда, когда размер системного стека (того, в который помещается адрес возврата и где выделяется память под локальные переменные) сильно ограничен какими-то аппаратными особенностями; в таких случаях реализуют стек самостоятельно и имитируют вызов подпрограммы путем работы с этим "доморощенным" стеком.

Тем не менее, аппаратный стек несколько быстрее, чем стек, реализованный самостоятельно. Поэтому в некоторых случаях, когда используется стек (например, для вычисления значения выражения, для перевода выражения из инфиксной в постфиксную форму и т.д.) небольших размеров, имеет смысл использовать рекурсию для того, что бы воспользоваться аппаратными возможностями по его организации.

Особенно стоит отметить, что при использовании рекурсивных подпрограмм важен вопрос о выделении памяти под локальные переменные. Все дело в том, что когда разворачивается рекурсивный вызов, на каждый конкретный вход в подпрограмму будет израсходована память под все локальные переменные. Это значит, что их использование должно быть сведено к минимуму, иначе память может закончиться раньше, чем вычислится значение выражения.