Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Статистические данные. Метод наименьших квадратов

Содержание

2. Статистика — наука о сборе, измерении и
3. Виды статистики:СоциальнаяЭкономическаяМедицинская и другие
4. Рассмотрим пример из медицинской статистики:
5. Специалисты по медицинской статистике проводят сбор данных.
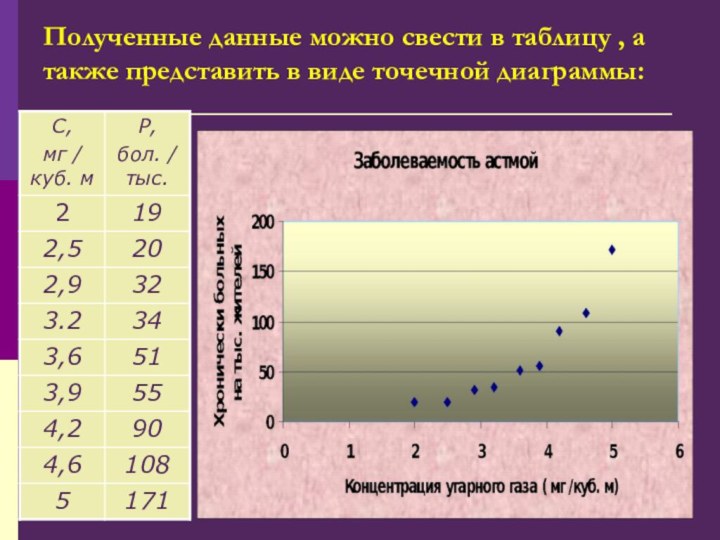
6. Полученные данные можно свести в таблицу , а также представить в виде точечной диаграммы:
7. Как построить математическую модель полученных данных?
8. Основные требования к искомой функции:Она должна быть
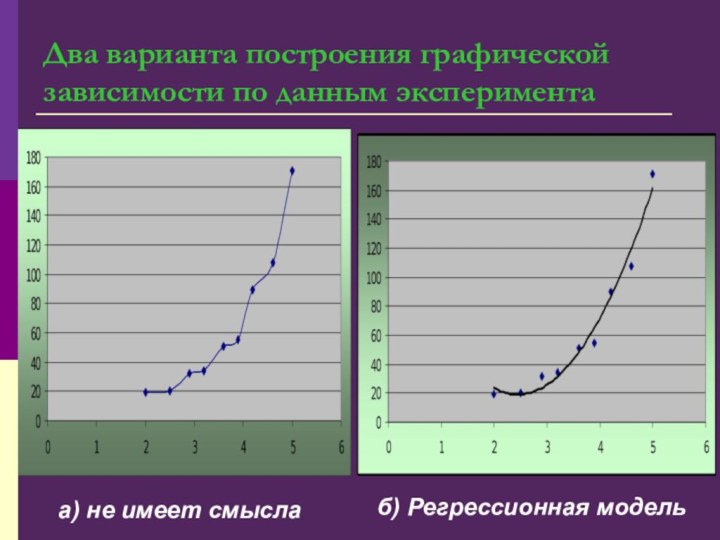
9. Два варианта построения графической зависимости по данным эксперимента а) не имеет смыслаб) Регрессионная модель
10. Регрессионная модель — это функция, описывающая
11. Этапы получения регрессионной модели:подбор вида функции;вычисление параметров функции.
12. Наиболее часто выбор производится среди функций:y =
13. Как подобрать параметры функции? Метод наименьших
14. R2 – коэффициент детерминированностиХарактеристикой построенной модели является
15. Тренд: это график регрессионной модели. Trend (англ.) – общее направление, тенденция.
19. Скачать презентацию
20. Похожие презентации

Статистика — наука о сборе, измерении и анализе массовых количественных данных. Статистические данные носят приближённый, усреднённый характер, получаются путём многократных измерений.

Главная
Информатика
Презентация Статистические данные. Метод наименьших квадратов

Статистические данные Метод наименьших квадратов11 класс

Статистика — наука о сборе, измерении и анализе массовых количественных данных.

Виды статистики:СоциальнаяЭкономическаяМедицинская и другие

Рассмотрим пример из медицинской статистики: Определить зависимость бронхиально-лёгочных заболеваний

Специалисты по медицинской статистике проводят сбор данных. Они собирают сведения из

Полученные данные можно свести в таблицу , а также представить в виде точечной диаграммы:

Как построить математическую модель полученных данных? Нужно получить формулу, отражающую зависимость

Основные требования к искомой функции:Она должна быть достаточно простой для использования её

Два варианта построения графической зависимости по данным эксперимента а) не имеет смыслаб) Регрессионная модель

Регрессионная модель — это функция, описывающая зависимость между количественными характеристиками сложных

Этапы получения регрессионной модели:подбор вида функции;вычисление параметров функции.

Наиболее часто выбор производится среди функций:y = ax + b — линейная

Как подобрать параметры функции? Метод наименьших квадратов (МНК) используется для вычисления

R2 – коэффициент детерминированностиХарактеристикой построенной модели является параметр R2 – коэффициент детерминированности.

Тренд: это график регрессионной модели. Trend (англ.) – общее направление, тенденция.

Презентация Статистические данные. Метод наименьших квадратов

Алгоритм построения регрессионной модели по МНК с построением тренда.Ввести табличные

Слайды презентации

Слайд 2 Статистика — наука о сборе, измерении и анализе

массовых количественных данных.
Статистические данные носят приближённый,

усреднённый характер, получаются путём многократных измерений.

Слайд 3 Виды статистики:
Социальная
Экономическая
Медицинская
и другие

Слайд 4 Рассмотрим пример из медицинской статистики:

Рассмотрим пример из медицинской статистики: Определить зависимость бронхиально-лёгочных заболеваний от

Определить зависимость бронхиально-лёгочных заболеваний от содержания угарного газа (оксида

углерода) в воздухе.

Слайд 5 Специалисты по медицинской статистике проводят сбор данных.

Они собирают сведения из разных городов о средней концентрации

угарного газа в атмосфере и о заболеваемости астмой — число хронически больных на 1000 жителей.

Слайд 6 Полученные данные можно свести в таблицу , а

также представить в виде точечной диаграммы:

Слайд 7 Как построить математическую модель полученных данных?
Нужно

получить формулу, отражающую зависимость числа хронически больных Р от

концентрации угарного газа С.

То есть — функцию зависимости Р от С: Р( С ).

Слайд 8 Основные требования к искомой функции:
Она должна быть достаточно

Основные требования к искомой функции:Она должна быть достаточно простой для использования

простой для использования её в дальнейших вычислениях;
График этой функции

должен проходить вблизи экспериментальных точек так, чтобы отклонения от этих точек были минимальны и равномерны.

Слайд 9 Два варианта построения графической зависимости по данным эксперимента

а) не имеет смысла
б) Регрессионная модель

Слайд 10 Регрессионная модель —
это функция, описывающая зависимость

между количественными характеристиками сложных систем.

Вид регрессионной

функции
определяется путём подбора по экспериментальным данным.

Слайд 11 Этапы получения регрессионной модели:
подбор вида функции;
вычисление параметров функции.

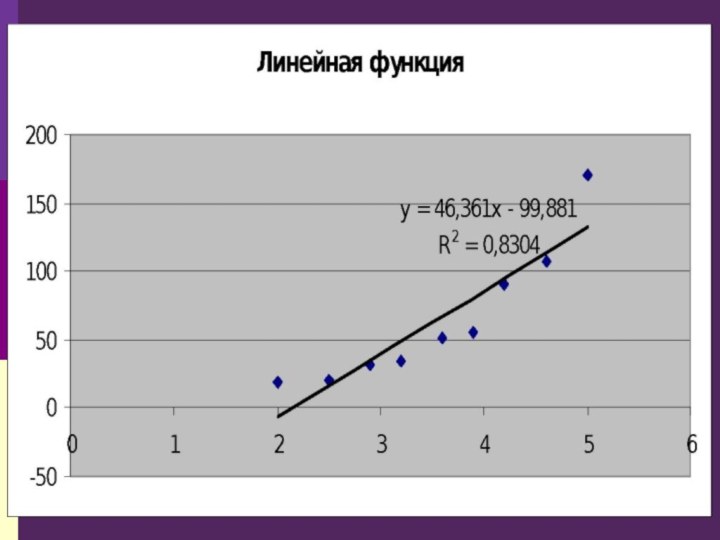
Слайд 12 Наиболее часто выбор производится среди функций:
y = ax

Наиболее часто выбор производится среди функций:y = ax + b —

+ b — линейная функция;
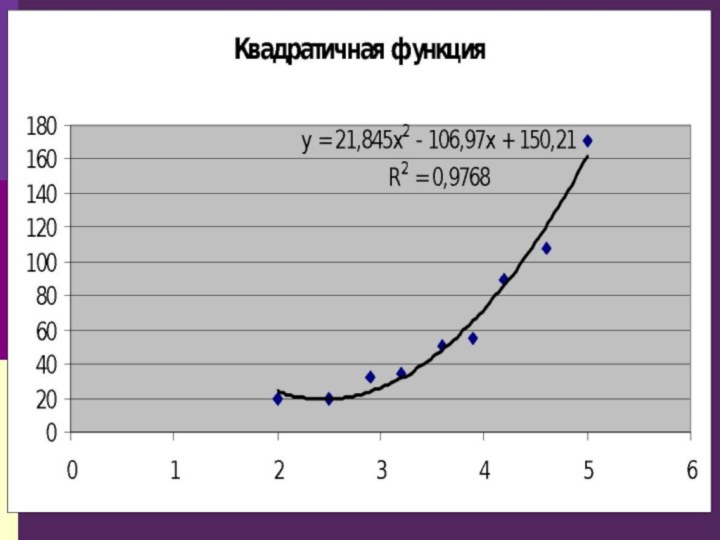
y = ax2 + bx

+ c — квадратичная функция (или полином второй степени);
y = aln(x)+ b — логарифмическая функция;
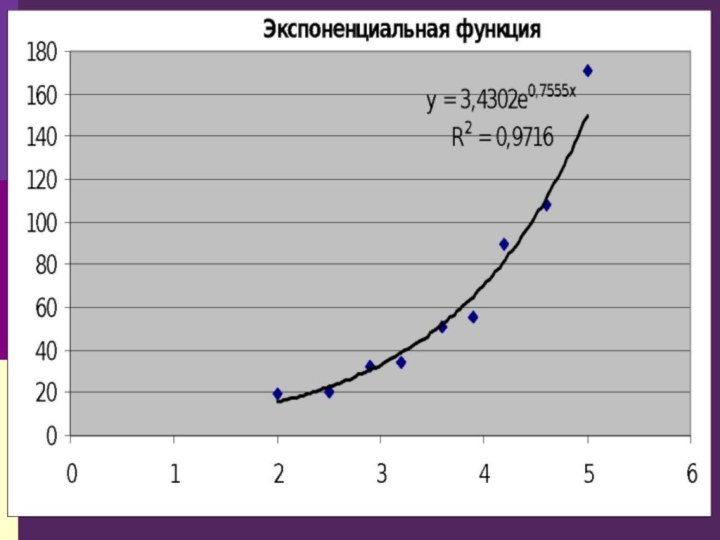
y = aebx — экспоненциальная функция;
y = axb— степенная функция.
Где x – аргумент, y – значение функции, a, b, c – параметры функции.