Презентация на тему Системы счисления. Перевод чисел из одной системы счисления в другую при помощи Калькулятора

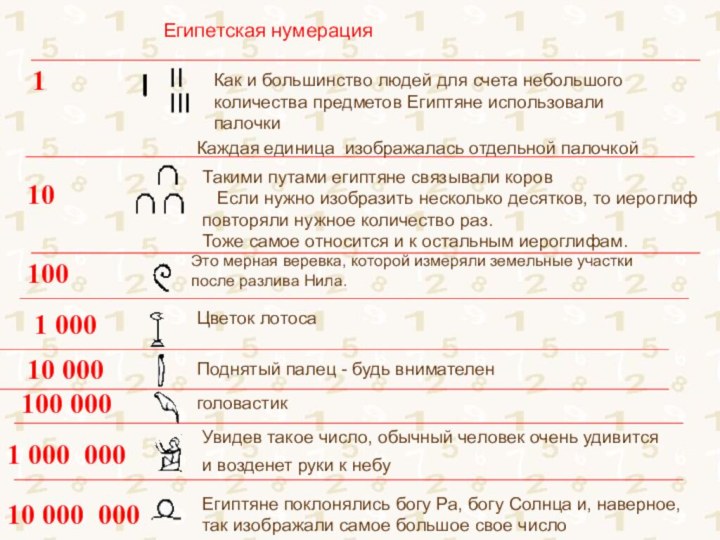
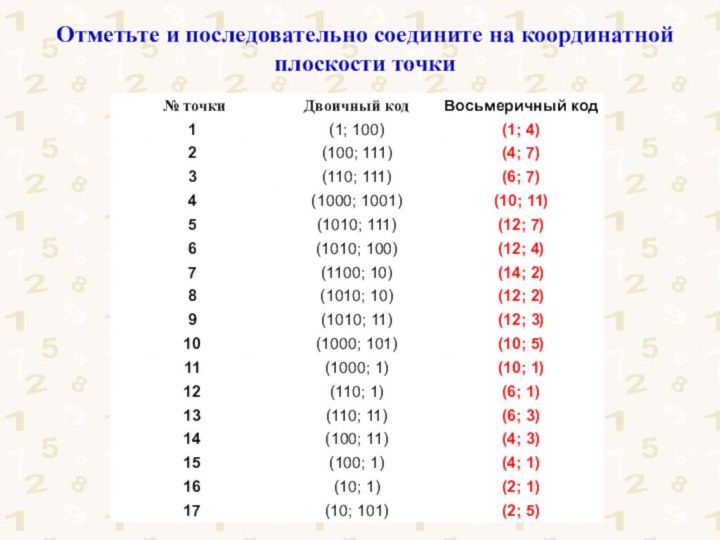
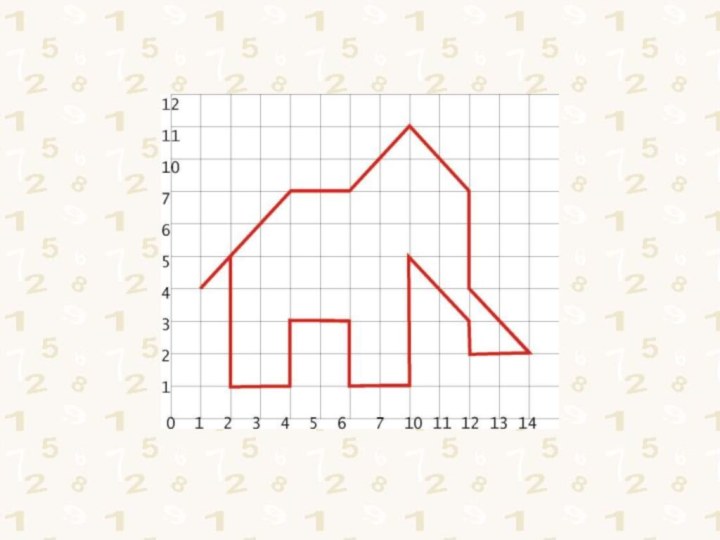
сородичей о количестве обнаруженных им предметов.
Сначала люди просто

Первыми понятиями математики были "меньше", "больше" и "столько же". Если одно племя меняло пойманных рыб на сделанные людьми другого племени каменные ножи, не нужно было считать, сколько принесли рыб и сколько ножей. Достаточно было положить рядом с каждой рыбой по ножу, чтобы обмен между племенами состоялся.

человека
С их помощью можно было считать до 5, а

общеупотребительной - десятичная.

могли пользоваться для счета пальцами как рук, так и

До сих пор существуют в Полинезии племена, которые для счета используют с 20-ую систему счисления

машине» рук и ног добавляли механические приспособления.
Способов счета

Например, перуанцы употребляли для запоминания чисел разноцветные шнуры с завязанными на них узлами.

т.д.

времена, как только люди научились считать. Количество предметов изображалось

=

Люди рисовали палочки на стенах и делали зарубки на костях животных или ветках деревьев

относящихся к периоду палеолита (10 - 11 тыс. лет

Египтяне придумали эту систему около 5 000 лет тому назад.

Египетская нумерация

предметов Египтяне использовали палочки
Каждая единица изображалась отдельной палочкой

Такими

1

10

Это мерная веревка, которой измеряли земельные участки после разлива Нила.

100

1 000

Цветок лотоса

Египетская нумерация

головастик

100 000

1 000 000

10 000 000

Египтяне поклонялись богу Ра, богу Солнца и, наверное, так изображали самое большое свое число

Увидев такое число, обычный человек очень удивится и возденет руки к небу

10 000

Поднятый палец - будь внимателен

выглядеть
1
2
4
5
3
8
6

запись чисел нового типа, так называемая алфавитная нумерация.
Алфавитная

В этой системе записи числа обозначались при помощи букв алфавита., над которыми ставились черточки: первые девять букв обозначали числа от 1 до 9, следующие девять - числа 10, 20, 30, ..., 90, и следующие девять - числа 100, 200, ..., 900.
Таким образом, можно было обозначать любое число до 999.

кириллическая нумерация

значки, которые дорисовывались к букве.
Алфавитная нумерация

числа на циферблате часов, и т. д. Возникла эта нумерация

Это нумерация, известная нам и в настоящее время. С нею мы достаточно часто сталкиваемся в повседневной жизни.

т. е. пять минус один,
восемь — VIII (пять

Правила записи чисел
Числа записывались слева направо, от больших к меньшим.
Если цифра с меньшим значением записывалась перед цифрой с большим значением, то происходило ее вычитание.
Нельзя было писать четыре одинаковые цифры подряд.

в их первоначальном варианте было придано значение в строгом

Арабская нумерация

Это, самая распространенная на сегодняшний день нумерация, которой мы пользуемся в настоящее время.
В России арабская нумерация стала использоваться
при Петре I (до конца XVII века сохранилась славянская нумерация)

чисел с помощью набора символов, называемых цифрами.
Количество цифр

Алфавит системы счисления - это совокупность цифр и букв, с помощью которых записываются числа.

цифре соответствует величина, не зависящая от её места в

Системы счисления, в которых вклад каждой цифры в величину числа зависит от её положения (позиции) в последовательности цифр, изображающей число

Древнегреческая, кириллическая, римская

Десятичная, двоичная и т.д.

записи чисел, в которых вклад каждой цифры в величину

Позиционные системы счисления результат длительного исторического развития непозиционных систем счисления

В римской записи числа важно не собственное положение цифры, а где она стоит относительно другой цифры:
записи XII и IX. Здесь в обоих случаях цифра "I" стоит на 2-ом месте справа, но в одном случае ее нужно прибавлять к 10, а в другом вычитать!

вводить новые цифры (буквы);
Трудно записывать большие числа;
Нельзя записывать дробные

для записи чисел;
Простота выполнения арифметических операций.

кодируются на машинном языке, в виде двоичного кода:

знаков одной знаковой системы в знаки или группы знаков

информации в виде 0 и 1

Двоичная система счисления является

чтобы понять, как самая разнообразная информация представлена в компьютере,

последовательности битов можно представить самую разную информацию. Такое представление

двоичной?
Компьютеры используют двоичную систему потому, что она имеет ряд

в другую позиционную систему, его последовательно делят на основание

последовательно делят на два и каждый раз записывают остаток:
12310=11110112

2 Выберите в меню Вид-Инженерный
3 Настройте НУЖНУЮ систему счисления
Автоматизированный

- восьмеричная
Bin (Binary) – двоичная

101011001
Перейдите в режим десятичной системы кнопкой Dec.
В окне ввода

Пример

отметьте 22 клеточки
По оси У отметьте 22 клеточки
Переведите координаты

Практическое задание

У вас получится картинка
А вот какая вам предстоит узнать!

Пример системы координат с готовым рисунком

координатной плоскости получилась звезда!

и У давайте напишем числа в восьмеричной системе счисления,

Практическое задание

Переведите координаты из двоичной системы в восьмеричную и запишите их
Отметьте все координаты точками и соедините точки последовательно
У вас получится картинка

Пример системы координат с готовым рисунком

7
Двоичная
2
Шестнадцатеричная
0;1;2;3;4;5;6;7;8;9;
A;B;C;D;E;F