Презентация на тему Анализ управляемой марковской системы массового обслуживания с неоднородными требованиями

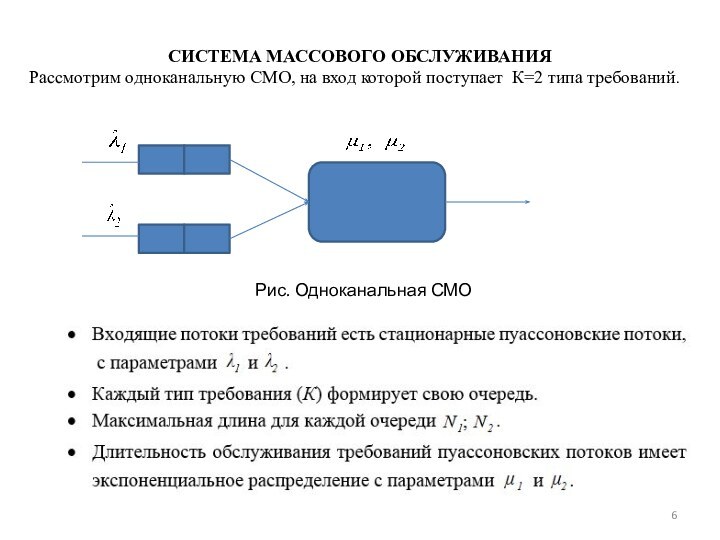
исследования: поиск оптимальной стратегии управления приоритетами в одноканальной система

массового обслуживания.
Цель исследования: построить оптимальную стратегию выбора динамического приоритета.


изучить математический аппарат, позволяющий провести анализ и обоснование оптимальной стратегии управления в СМО;
проанализировать факторы и построить математическую модель функционирования системы массового обслуживания с несколькими потоками неоднородных требований;
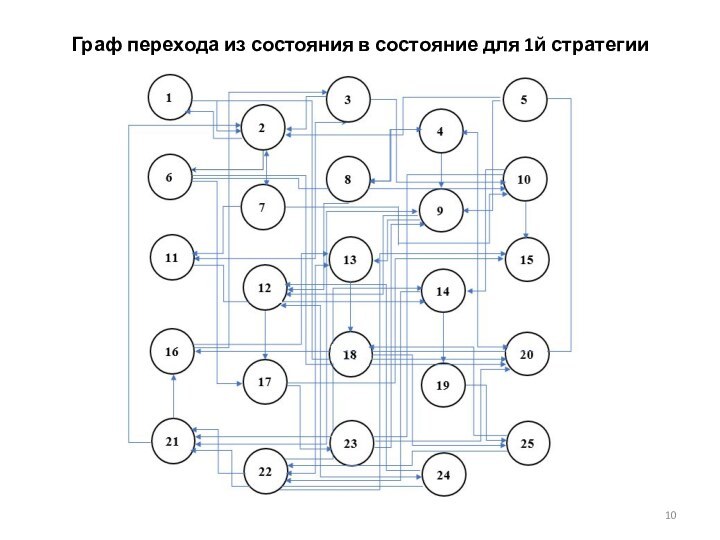
исследовать управляемую марковскую систему массового обслуживания с приоритетами;
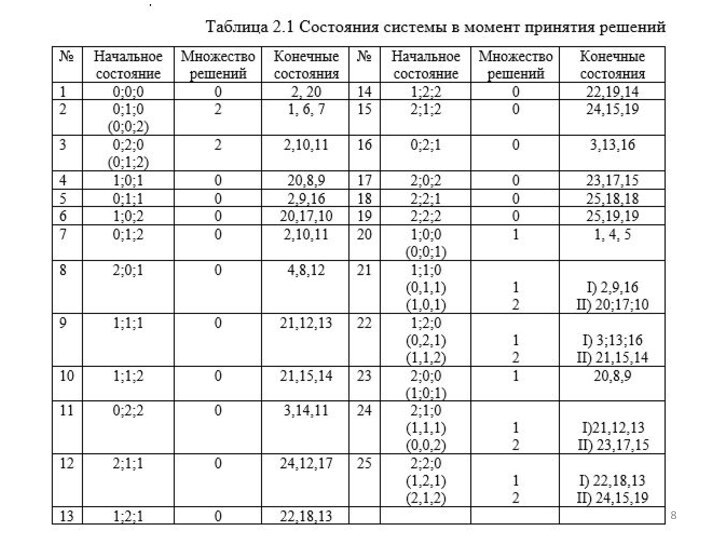
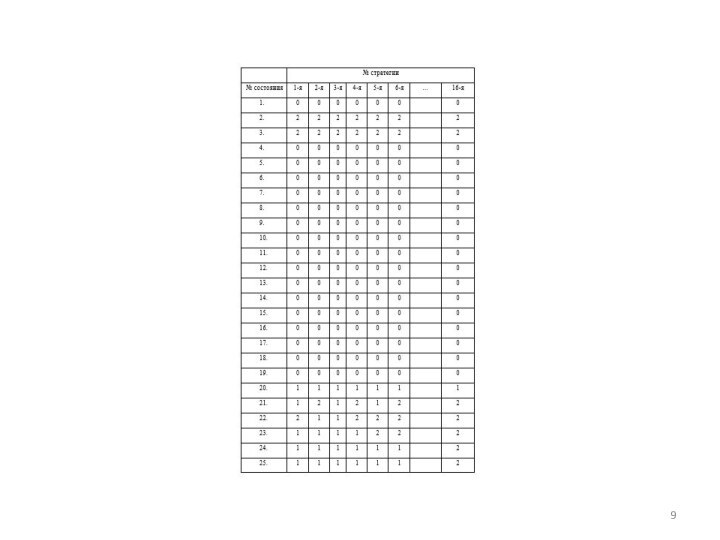
построить алгоритм определения оптимальной стратегии управления
реализовать вычислительный эксперимент;
проанализировать полученный результат.

Задачи исследования:

Объект. Предмет. Цель.

с конечным множеством состояний Е


Траектории этих компонент, есть ступенчатые

функции и точки разрывов совпадают.
Моменты изменения состояний (скачки) являются Марковскими моментами.
Время непрерывного пребывания в фиксированном состоянии для Марковского процесса имеет экспоненциальное распределение.
Время непрерывного пребывания для полумарковского процесса имеет произвольное распределение.
Случайный процесс задается характеристиками:
Полумарковское ядро - вероятность того, что первая компонента перейдет в состояние j, за время меньшее чем t при условии, что в данный момент состояние i и принято решение u.
Набор вероятностных мер , определенных на сигма алгебрах подмножеств множеств (стратегия управления).

математическими ожиданиями накопленного эффекта

на периоде между соседними моментами изменения состояний полумарковского процесса при условии, что процесс пребывает в состоянии i, переходит в состояние j, длительность периода равна t и на этом периоде было принято решение u.
S(t) – математическое ожидание накопленного эффекта за время t.

- средний удельный доход при длительном функционировании системы,

где


математическое ожидание накопленного эффекта за полное время пребывания в состоянии i.

- стационарные вероятности

состояний вложенной цепи Маркова.







Тогда задача состоит в поиске максимума и распределении на котором достигается максимум

,
причем экстремум можно искать по множеству вырожденных распределений

поступает К=2 типа требований.
Рис. Одноканальная СМО

описание системы
Марковские моменты прихода и ухода требований из системы.

Первая компонента случайного Марковского процесса определяется равенством:

- количество занятых мест в первой очереди;
- количество занятых мест во второй очереди;

если обслуживается требование из первой очереди
если обслуживается требование из второй очереди
если канал свободен

стратегии

число обслуживающих приборов
Число мест для ожидания
Стоимостные характеристики:

доход (прибыль) соответствующий выбранной стратегии.
Рис. 1 График зависимости прибыли

от стратегии

Первая часть вычислительной реализации заключается в следующем: изменяя описанные выше стратегии (16 вырожденных стратегий) для заданных исходных числовых параметров, определить математическое ожидание удельного дохода.
Результаты вычислений приведены на Рис. 1

принятии (первой стратегии (рис. 1)) решений:
в состоянии 21 принимается

решение первым взять на обслуживание требование 1-го типа;
в состоянии 22 принимается решение первым взять на обслуживание требование 2-го типа;
в состоянии 24 принимается решение первым взять на обслуживание требование 1-го типа;
в состоянии 25 принимается решение первым взять на обслуживание требование 1-го типа;
а в остальных стратегиях с вероятностью единица принимается единственное решение.

Вторая часть вычислительного эксперимента заключается в варьировании числовых исходных данных и определении оптимального дохода (при выборе оптимальной стратегии).
При фиксировании исходных показателей, кроме дохода за обслуженное требование первого типа, и увеличивая его от 9 до 500.

обслуживание I-го типа требования.
Ось x – дохода за обслуживание

I-го типа требований.
Ось y – оптимальный S доход (прибыль), соответствующий выбранным значениям параметров.

вычислительного эксперимента получили, что оптимальная стратегия одна и та

же, а при изменении одного из числовых параметров, оптимальных доход – есть линейная функция этого параметра, что соответствует теоретическим рассуждениям.