практических умений и навыков.
Формы работы на уроке: самостоятельная,
парная и индивидуальная работа. Методы: словесный (рассказ), наглядный, диалогический.
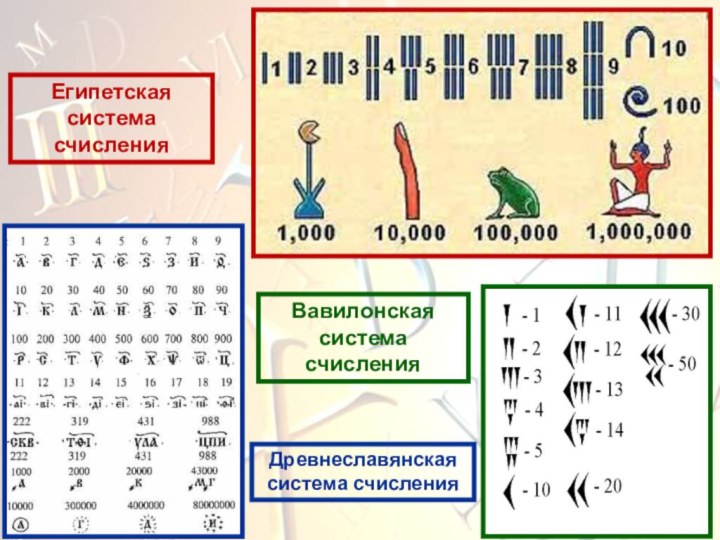
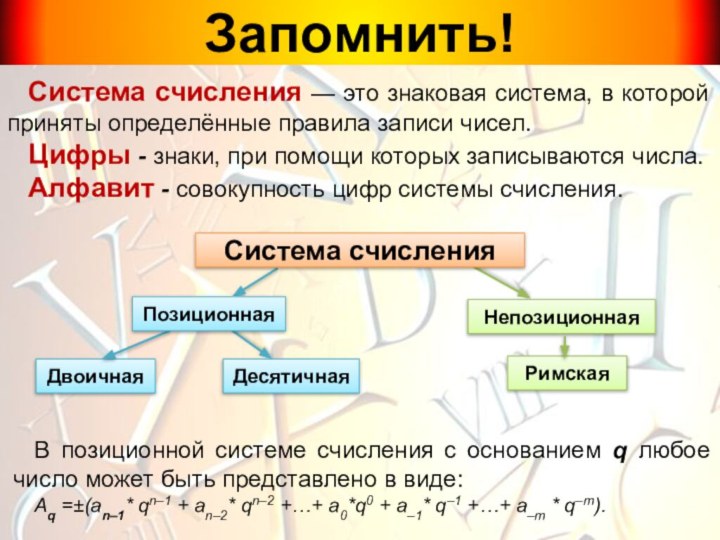
Основные понятия: системы счисления, позиционная, непозиционная, разряд, свернутая, развернутая формы записи числа.






































![Презентация по информатике Представление числовой информации с помощью систем счисления, 10 класс Список источников содержания и иллюстрацийhttp://school-collection.edu.ru/catalog/res/402b749c-240b-4e16-9e4d-bea3fc4fa8fa/?from=a30a9550-6a62-11da-8cd6-0800200c9a66&interface=catalog&class=51&subject=19&rub_guid[]=a30a9550-6a62-11da-8cd6-0800200c9a66 – История развития систем счисленияhttp://school-collection.edu.ru/catalog/res/a96df437-5ae3-4cab-8c5f-8d4cd78c5775/?from=a30a9550-6a62-11da-8cd6-0800200c9a66&interface=catalog&class=51&subject=19&rub_guid[]=a30a9550-6a62-11da-8cd6-0800200c9a66 –http://www.wikiznanie.ru/ Развернутая форма записи числаhttp://go.mail.ru/http://go.mail.ru/ https://ru.wikipedia.orghttp://inf1.info/scalenotation](/img/tmb/7/616980/4938ac0fcde05d5cae6e21358cb19a23-720x.jpg)





























