- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Анализ программы с подпрограммами
Содержание
- 2. Анализ программы с подпрограммамиЧто нужно знать.Примеры заданий:Пример 1Пример 2Пример 3Задания для тренировки.
- 3. Нужно знать, что:Функция – это вспомогательный алгоритм,
- 4. function F(x: integer):integer; begin
- 5. function F(x: integer):integer; begin
- 6. Если параметров несколько, для каждого из
- 7. Следующая программа ищет наименьшее значение функции
- 8. Цикл для поиска наибольшего значения выглядит
- 9. Если функция представляет собой квадратный трехчлен
- 10. Определите, какое число будет напечатано в результате
- 11. Определите, какое число будет напечатано в результате
- 12. Определите, какое число будет напечатано в результате
- 13. Определите, какое число будет напечатано в результате
- 14. Определите, какое число будет напечатано в результате
- 15. Определите, какое число будет напечатано в результате
- 16. Определите, какое число будет напечатано в результате
- 17. F:=4*(t-1)*(t-3) По таблице находим, что минимальное значение –4 достигается при t=2 Таким образом, ответ: 2.Пример 1.
- 18. Рассмотрим решение 2 (математический анализ):
- 19. Определите, какое число будет напечатано в результате
- 20. Определите, какое число будет напечатано в результате
- 21. График этой функции – парабола, оси которой
- 22. Определите, какое число будет напечатано в результате
- 23. График этой функции – парабола, оси которой
- 24. Определите, какое число будет напечатано в результате
- 25. Определите, какое число будет напечатано в результате
- 26. График этой функции – парабола, ветви которой
- 27. Пример 3.Определите, какое число будет напечатано в
- 28. Пример 3.Определите, какое число будет напечатано в
- 29. Пример 3.Определите, какое число будет напечатано в
- 30. График этой функции – парабола, оси
- 31. -200Пример 2.При t=-20 получаем F(-20)=4*(-21)*(-23)=1932При t=0 получаем
- 32. Задачи для тренировки: Источники заданий: Демонстрационные варианты ЕГЭ 2012-2013 гг.Тренировочные работы МИОО.Разработки К. Полякова
- 33. Определите, какое число будет напечатано в результате
- 34. Определите, какое число будет напечатано в результате
- 35. Определите, какое число будет напечатано в результате
- 36. Определите, какое число будет напечатано в результате
- 37. Определите, какое число будет напечатано в результате
- 38. Определите, какое число будет напечатано в результате
- 39. Определите, какое число будет напечатано в результате
- 40. Определите, какое число будет напечатано в результате
- 41. Определите, какое число будет напечатано в результате
- 42. Определите, какое число будет напечатано в результате
- 43. Определите, какое число будет напечатано в результате
- 44. Определите, какое число будет напечатано в результате
- 45. Определите, какое число будет напечатано в результате
- 46. Определите, какое число будет напечатано в результате
- 47. Определите, какое число будет напечатано в результате
- 48. Определите, какое число будет напечатано в результате
- 49. Определите, какое число будет напечатано в результате
- 50. Определите, какое число будет напечатано в результате
- 51. Определите, какое число будет напечатано в результате
- 52. Определите, какое число будет напечатано в результате
- 53. Определите, какое число будет напечатано в результате
- 54. Определите, какое число будет напечатано в результате
- 55. Определите, какое число будет напечатано в результате
- 56. Определите, какое число будет напечатано в результате
- 57. Определите, какое число будет напечатано в результате
- 58. Определите, какое число будет напечатано в результате
- 59. Скачать презентацию
- 60. Похожие презентации






![Анализ программы с подпрограммами Следующая программа ищет наименьшее значение функции F(x) на отрезке [a,b], просматривая](/img/tmb/7/631635/e66d9adb0ff9330ae2a1103c6e871b4b-720x.jpg)


















































Слайд 3
Нужно знать, что:
Функция – это вспомогательный алгоритм, который
возвращает некоторое значение –результат.
В Паскале функция располагается выше основной
программы и оформляется следующим образом (вместо многоточия могут быть любые операторы):function F(x: integer):integer;
begin
...
F:= <результат функции>
end;
Слайд 4
function F(x: integer):integer;
begin
...
F:=
end;
В заголовке функции записывают имя функции, в скобках – список параметров, далее через двоеточие – тип возвращаемого значения; в приведенном примере функция F принимает один целый параметр, к которому внутри функции нужно обращаться по имени x, и возвращает целое число.
Слайд 5
function F(x: integer):integer;
begin
...
F:=
end;
Результат функции записывается в специальную переменную, имя которой совпадает с именем функции; объявлять эту переменную не нужно.Слайд 6 Если параметров несколько, для каждого из них
указывают тип:
function F(x: integer; y: integer):integer;
Если несколько соседних
параметров имеют одинаковый тип, можно их объединить в список:function F(x, y: integer):integer;
Слайд 7 Следующая программа ищет наименьшее значение функции F(x)
на отрезке [a,b], просматривая значения от a до b
с шагом 1:M:=a; R:=F(a);
for t:=a to b do
if F(t) < R then
begin
R:=F(t); M:=t;
end;
Слайд 8 Цикл для поиска наибольшего значения выглядит точно
так же, только знак < нужно заменить на знак
>:M:=a; R:=F(a);
for t:=a to b do
if F(t) > R then
begin
R:=F(t); M:=t;
end;
Слайд 9 Если функция представляет собой квадратный трехчлен вида
, то абсцисса, соответствующая точке минимума, вычисляется по формуле
Если квадратный трехчлен задан в виде
то абсцисса, соответствующая точке минимума, вычисляется по формуле
,
Слайд 10 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:=4*(x-1)*(x-3);
end;
BEGIN
a:=-20; b:=20;
M:=a; R:=F(a);for t:=a to b do
begin
if (F(t)
M:=t;
R:=F(t);
end;
end;
write(M);
END.
Решение 1 (ручная прокрутка):
Пример 1.
Слайд 11 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:=4*(x-1)*(x-3);
end;
BEGIN
a:=-20; b:=20;
M:=a; R:=F(a);for t:=a to b do
begin
if (F(t)
M:=t;
R:=F(t);
end;
end;
write(M);
END.
Решение 1 (ручная прокрутка):
Заметим, что в программе есть цикл, в котором переменная t принимает последовательно все целые значения в интервале
от a до b.
Пример 1.
Слайд 12 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:=4*(x-1)*(x-3);
end;
BEGIN
a:=-20; b:=20;
M:=a; R:=F(a);for t:=a to b do
begin
if (F(t)
M:=t;
R:=F(t);
end;
end;
write(M);
END.
Решение 1 (ручная прокрутка):
До начала цикла в переменную M записывается значение a, а в переменную R – значение функции в точке a.
Пример 1.
Слайд 13 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:=4*(x-1)*(x-3);
end;
BEGIN
a:=-20; b:=20;
M:=a; R:=F(a);for t:=a to b do
begin
if (F(t)
M:=t;
R:=F(t);
end;
end;
write(M);
END.
Решение 1 (ручная прокрутка):
Внутри цикла есть условный оператор, в котором вычисляется значение функции F(t) и сравнивается со значением переменной R.
Пример 1.
Слайд 14 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:=4*(x-1)*(x-3);
end;
BEGIN
a:=-20; b:=20;
M:=a; R:=F(a);for t:=a to b do
begin
if (F(t)
M:=t;
R:=F(t);
end;
end;
write(M);
END.
Решение 1 (ручная прокрутка):
Если новое значение функции меньше, чем значение R, в R записывается значение функции в точке t, а в переменной M запоминается само значение t (аргумент функции, соответствующий значению в R)
Пример 1.
Слайд 15 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:=4*(x-1)*(x-3);
end;
BEGIN
a:=-20; b:=20;
M:=a; R:=F(a);for t:=a to b do
begin
if (F(t)
M:=t;
R:=F(t);
end;
end;
write(M);
END.
Решение 1 (ручная прокрутка):
Следовательно, цикл ищет минимум функции F(t) на интервале от a до b, и после выполнения цикла в переменной M оказывается значение аргумента t, при котором функция достигает минимума на заданном интервале
(здесь это интервал [-20, 20])
Пример 1.
Слайд 16 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:=4*(x-1)*(x-3);
end;
BEGIN
a:=-20; b:=20;
M:=a; R:=F(a);for t:=a to b do
begin
if (F(t)
M:=t;
R:=F(t);
end;
end;
write(M);
END.
Решение 1 (ручная прокрутка):
Функция F вычисляет значение
F:=4*(x-1)*(x-3)
Перебираем все значения t от a до b, и для каждого вычисляем соответствующее значение функции:
Пример 1.
Слайд 17
F:=4*(t-1)*(t-3)
По таблице находим, что минимальное значение –4
достигается при t=2
Таким образом, ответ: 2.
Пример 1.
Слайд 19 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:=4*(x-1)*(x-3);
end;
BEGIN
a:=-20; b:=20;
M:=a; R:=F(a);for t:=a to b do
begin
if (F(t)
M:=t;
R:=F(t);
end;
end;
write(M);
END.
Повторяя рассуждения из предыдущего способа решения, находим, что программа ищет значение t, при котором функция F(t) принимает минимальное значение на интервале от a до b.
Запишем функцию в виде квадратного трёхчлена:
Решение 2
(математический анализ):
Пример 1.
Слайд 20 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:=4*(x-1)*(x-3);
end;
BEGIN
a:=-20; b:=20;
M:=a; R:=F(a);for t:=a to b do
begin
if (F(t)
M:=t;
R:=F(t);
end;
end;
write(M);
END.
Повторяя рассуждения из предыдущего способа решения, находим, что программа ищет значение t, при котором функция F(t) принимает минимальное значение на интервале от a до b.
Запишем функцию в виде квадратного трёхчлена:
Решение 2
(математический анализ):
Пример 1.
Слайд 21 График этой функции – парабола, оси которой направлены
вверх, поэтому функция имеет минимум.
Найдем абсциссу точки минимума,
которая совпадает с абсциссой точки минимума функции: Таким образом, ответ: 2.
Пример 1.
-20
20
Слайд 22 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:=4*(x-1)*(x-3);
end;
BEGIN
a:=-20; b:=20;
M:=a; R:=F(a);for t:=a to b do
begin
if (F(t)
M:=t;
R:=F(t);
end;
end;
write(M);
END.
Повторяя рассуждения из предыдущего способа решения, находим, что программа ищет значение t, при котором функция F(t) принимает минимальное значение на интервале от a до b.
Заданная функция
имеет корни в точках
Решение 3
(свойства параболы):
Пример 1.
Слайд 23
График этой функции – парабола, оси которой направлены
вверх, поэтому функция имеет минимум.
Парабола симметрична относительно вертикальной
прямой, проходящей через вершину, поэтому абсцисса вершины – это среднее арифметическое корней:Таким образом, ответ: 2.
Пример 1.
1
3
Слайд 24 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R : integer;
Function F(x:integer): integer;
begin
F:=x*x
+ 4*x + 8;end;
BEGIN
a:=-10; b:=10;
M:=a; R:=F(a);
for t:=a to b do
begin
if (F(t)> R) then
begin
M:=t;
R:=F(t);
end;
end;
write(R);
END.
Решение:
Рассуждая так же, как и в предыдущем примере, можно показать, что программа ищет наибольшее значение функции F(t) на интервале от a до b
Пример 2.
Слайд 25 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R : integer;
Function F(x:integer): integer;
begin
F:=x*x
+ 4*x + 8;end;
BEGIN
a:=-10; b:=10;
M:=a; R:=F(a);
for t:=a to b do
begin
if (F(t)> R) then
begin
M:=t;
R:=F(t);
end;
end;
write(R);
END.
Решение:
Заметим, что выводится не абсцисса, а именно это найденное наибольшее значение функции!!!
Пример 2.
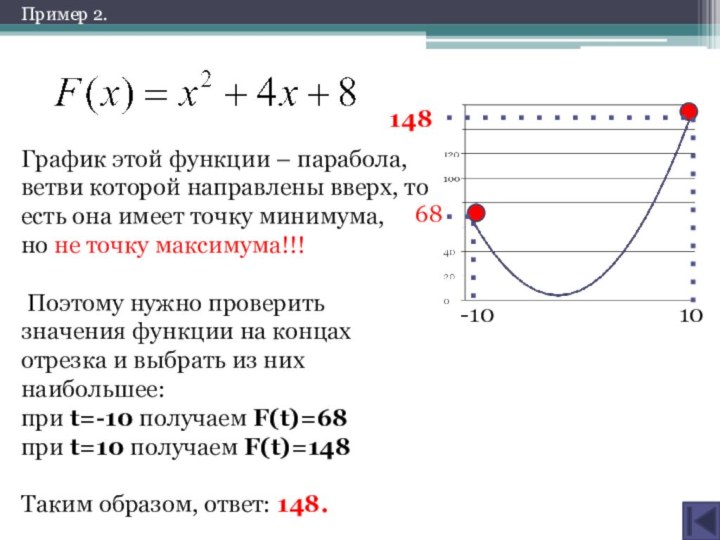
Слайд 26
График этой функции – парабола, ветви которой направлены
вверх, то есть она имеет точку минимума,
но не
точку максимума!!!Поэтому нужно проверить
значения функции на концах отрезка и выбрать из них наибольшее:
при t=-10 получаем F(t)=68
при t=10 получаем F(t)=148
Таким образом, ответ: 148.
-10
10
Пример 2.
148
68
Слайд 27
Пример 3.
Определите, какое число будет напечатано в результате
выполнения следующего алгоритма:
Var a,b,t,M,R : integer;
Function F(x:integer): integer;
begin
F:=4*(x-1)*(x-3);end;
BEGIN
a:=-20; b:=0;
M:=a; R:=F(a);
for t:=a to b do
begin
if (F(t)
M:=t;
R:=F(t);
end;
end;
write(M);
END.
Слайд 28
Пример 3.
Определите, какое число будет напечатано в результате
выполнения следующего алгоритма:
Var a,b,t,M,R : integer;
Function F(x:integer): integer;
begin
F:=4*(x-1)*(x-3);end;
BEGIN
a:=-20; b:=0;
M:=a; R:=F(a);
for t:=a to b do
begin
if (F(t)
M:=t;
R:=F(t);
end;
end;
write(M);
END.
Решение:
Рассуждая так же, как и в примере 1, определяем, что программа ищет значение t, при котором функция F(t) принимает минимальное значение на интервале
от a до b.
Слайд 29
Пример 3.
Определите, какое число будет напечатано в результате
выполнения следующего алгоритма:
Var a,b,t,M,R : integer;
Function F(x:integer): integer;
begin
F:=4*(x-1)*(x-3);end;
BEGIN
a:=-20; b:=0;
M:=a; R:=F(a);
for t:=a to b do
begin
if (F(t)
M:=t;
R:=F(t);
end;
end;
write(M);
END.
Решение:
Рассуждая так же, как и в примере 1, определяем, что программа ищет значение t, при котором функция F(t) принимает минимальное значение на интервале
от a до b.
Запишем функцию в виде квадратного трёхчлена:
Слайд 30
График этой функции – парабола, оси которой
направлены вверх, поэтому функция имеет минимум.
Найдем абсциссу точки
минимума, которая совпадает с абсциссой точки минимума функции: -20
0
Пример 2.
Однако это значение не входит в интервал [-20; 0],
поэтому нужно проверить значения функции на концах отрезка и выбрать из них наименьшее; ответом будет соответствующее значение t.
Слайд 31
-20
0
Пример 2.
При t=-20 получаем F(-20)=4*(-21)*(-23)=1932
При t=0 получаем F(0)=
4*(-1)*(-3)=12, это значение меньше, чем F(-20), поэтому минимум на
заданном интервале достигается при t=0Таким образом, ответ: 0.
1932
12
Слайд 32
Задачи для тренировки:
Источники заданий:
Демонстрационные варианты ЕГЭ 2012-2013
гг.
Тренировочные работы МИОО.
Разработки К. Полякова
Слайд 33 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer): integer;
begin
F:=4*(x-5)*(x+3);
end;
BEGIN
a:=-20;
b:=20;M:=a; R:=F(a);
for t:=a to b do begin
if (F(t)
R:=F(t);
end;
end;
write(M);
END.
Пример 1.
Ответ: 1
Слайд 34 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:=-(x+4)*(x+2);
end;
BEGIN
a:=-20; b:=20;
M:=a; R:=F(a);for t:=a to b do begin
if (F(t)>R)then begin
M:=t;
R:=F(t);
end;
end;
write(M);
END.
Пример 2.
Ответ: -3
Слайд 35 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:=3*(x-2)*(x+6);
end;
BEGIN
a:=-20; b:=20;
M:=a; R:=F(a);for t:=a to b do begin
if (F(t)
R:=F(t);
end;
end;
write(R);
END.
Пример 3.
Ответ: -48
Слайд 36 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:=(5-x)*(x+3);
end;
BEGIN
a:=-20; b:=20;
M:=a; R:=F(a);for t:=a to b do begin
if (F(t)>R)then begin
M:=t;
R:=F(t);
end;
end;
write(R);
END.
Пример 4.
Ответ: 16
Слайд 37 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:=(x-5)*(x+3);
end;
BEGIN
a:=-5; b:=5;
M:=a; R:=F(a);for t:=a to b do begin
if (F(t)>R)then begin
M:=t;
R:=F(t);
end;
end;
write(M);
END.
Пример 5.
Ответ: -5
Слайд 38 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:=(x+5)*(x+3);
end;
BEGIN
a:=-5; b:=5;
M:=a; R:=F(a);for t:=a to b do begin
if (F(t)>R)then begin
M:=t;
R:=F(t);
end;
end;
write(R);
END.
Пример 6.
Ответ: 80
Слайд 39 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:=(x+7)*(1-x);
end;
BEGIN
a:=-5; b:=5;
M:=a; R:=F(a);for t:=a to b do begin
if (F(t)< R)then begin
M:=t;
R:=F(t);
end;
end;
write(M);
END.
Пример 7.
Ответ: 5
Слайд 40 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:=(x+5)*(1-x);
end;
BEGIN
a:=-5; b:=5;
M:=a; R:=F(a);for t:=a to b do begin
if (F(t)< R)then begin
M:=t;
R:=F(t);
end;
end;
write(M);
END.
Пример 8.
Ответ: 5
Слайд 41 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:=(x+3)*(1-x);
end;
BEGIN
a:=-5; b:=5;
M:=a; R:=F(a);for t:=a to b do begin
if (F(t)< R)then begin
M:=t;
R:=F(t);
end;
end;
write(R);
END.
Пример 9.
Ответ: -32
Слайд 42 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:= 2*x*x +
8*x + 10;end;
BEGIN
a:=-10; b:=10;
M:=a; R:=F(a);
for t:=a to b do begin
if (F(t)< R)then begin
M:=t;
R:=F(t);
end;
end;
write(M);
END.
Пример 10.
Ответ: -2
Слайд 43 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:= x*x +
6*x + 10;end;
BEGIN
a:=-10; b:=10;
M:=a; R:=F(a);
for t:=a to b do begin
if (F(t)> R)then begin
M:=t;
R:=F(t);
end;
end;
write(M);
END.
Пример 11.
Ответ: 10
Слайд 44 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:= x*x -
8*x + 10;end;
BEGIN
a:=-5; b:=5;
M:=a; R:=F(a);
for t:=a to b do begin
if (F(t)> R)then begin
M:=t;
R:=F(t);
end;
end;
write(R);
END.
Пример 12.
Ответ: 75
Слайд 45 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:= x*x +
2*x + 10;end;
BEGIN
a:=-10; b:=10;
M:=a; R:=F(a);
for t:=a to b do begin
if (F(t)< R)then begin
M:=t;
R:=F(t);
end;
end;
write(M);
END.
Пример 13.
Ответ: -1
Слайд 46 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:=4*(x-5)*(x+3);
end;
BEGIN
a:=-20; b:=0;
M:=a; R:=F(a);for t:=a to b do begin
if (F(t)
R:=F(t);
end;
end;
write(M);
END.
Пример 14.
Ответ: 0
Слайд 47 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:= 2*x*x +
8*x + 10;end;
BEGIN
a:=0; b:=10;
M:=a; R:=F(a);
for t:=a to b do begin
if (F(t)< R)then begin
M:=t;
R:=F(t);
end;
end;
write(R);
END.
Пример 15.
Ответ: 10
Слайд 48 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:=-(x+4)*(x+2);
end;
BEGIN
a:=-2; b:=20;
M:=a; R:=F(a);for t:=a to b do begin
if (F(t)>R)then begin
M:=t;
R:=F(t);
end;
end;
write(M);
END.
Пример 16.
Ответ: -2
Слайд 49 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
var a,b,t,M,R :integer;
Function F(x: integer):integer;
begin
F :=
2*(x-9)*(x-9)+12;end;
BEGIN
a := -20; b := 20;
M := a; R := F(a);
for t := a to b do
if (F(t)
R := F(t);
end;
write(M);
END.
Пример 17.
Ответ: 9
Слайд 50 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
var a,b,t,M,R :integer;
Function F(x: integer):integer;
begin
F :=
9*(x-15)*(x+17)+2;end;
BEGIN
a := -20; b := 20;
M := a; R := F(a);
for t := a to b do
if (F(t)
R := F(t);
end;
write(M);
END.
Пример 18.
Ответ: -1
Слайд 51 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
var a,b,t,M,R :integer;
Function F(x: integer):integer;
begin
F :=
-3*(x-10)*(x+2)+2;end;
BEGIN
a := -20; b := 20;
M := a; R := F(a);
for t := a to b do
if (F(t)>R) then begin
M := t;
R := F(t);
end;
write(M);
END.
Пример 19.
Ответ: 4
Слайд 52 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
var a,b,t,M,R :integer;
Function F(x: integer):integer;
begin
F :=
5*(x+10)*(x+2)+2;end;
BEGIN
a := -20; b := 20;
M := a; R := F(a);
for t := a to b do
if (F(t)
R := F(t);
end;
write(M);
END.
Пример 20.
Ответ: -6
Слайд 53 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
var a,b,t,M,R :integer;
Function F(x: integer):integer;
begin
F :=
-2*(x+2)*(x-6);end;
Begin
a := -11; b := 11;
M := a; R := F(a);
t:=a;
while t < b do
begin
if (F(t)>R) then
begin
M := t;
R := F(t);
end;
t:=t+2;
end;
write(R);
End.
Пример 21.
Ответ: 30
Слайд 54 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
var a,b,t,M,R :integer;
Function F(x: integer):integer;
begin
F :=
-2*(x+2)*(x-6);end;
Begin
a := -11; b := 11;
M := a; R := F(a);
t:=a;
while t < b do
begin
if (F(t)>R) then
begin
M := t;
R := F(t);
end;
t:=t+2;
end;
write(M);
End.
Пример 22.
Ответ: 1
Слайд 55 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
var a,b,t,M,R :integer;
Function F(x: integer):integer;
begin
F :=
-2*(x+2)*(x-6);end;
Begin
a := -11; b := 11;
M := a; R := F(a);
t:=a;
while t < b do
begin
if (F(t)>=R) then
begin
M := t;
R := F(t);
end;
t:=t+2;
end;
write(M);
End.
Пример 23.
Ответ: 3
Слайд 56 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F := 3*(x-8)*(x-8)
end;
begin
a := -20; b := 20;M := a; R := F(a);
for t := a to b do begin
if (F(t)
R := F(t)
end
end;
write(M);
end.
Пример 24.
Ответ: 8
Слайд 57 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
var a,b,t,M,R :integer;
Function F(x: integer):integer;
begin
F :=
19*(16-x)*(16-x)+27;end;
BEGIN
a := -20; b := 20;
M := a; R := F(a);
for t := a to b do begin
if (F(t) < R) then begin
M := t;
R := F(t);
end;
end;
write(M);
END.
Пример 25.
Ответ: 16
Слайд 58 Определите, какое число будет напечатано в результате выполнения
следующего алгоритма:
var a,b,t,M,R :integer;
Function F(x: integer):integer;
begin
F :=
19*(11-x)*(11-x)+27;end;
BEGIN
a := -20; b := 20;
M := a; R := F(a);
for t := a to b do begin
if (F(t) < R) then begin
M := t;
R := F(t);
end;
end;
write(R);
END.
Пример 26.
Ответ: 27