Презентация на тему Целочисленные алгоритмы (язык Паскаль)

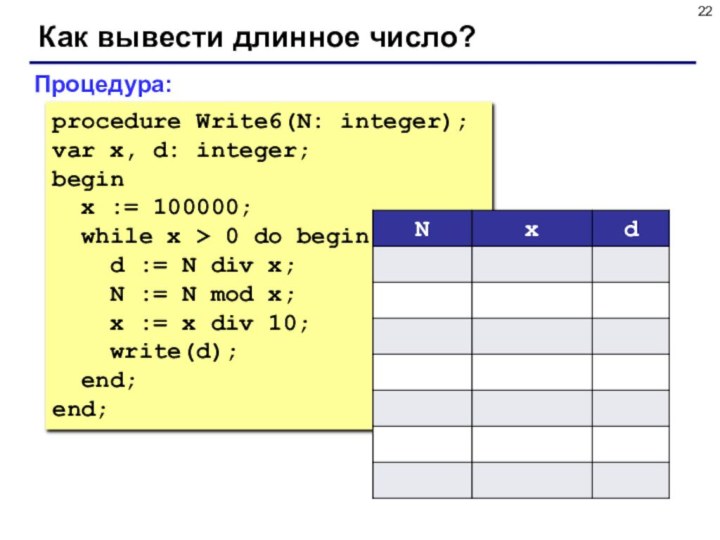
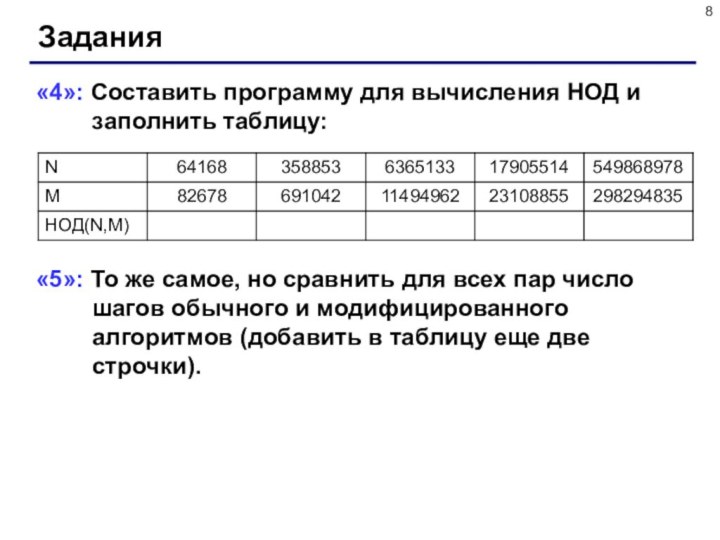
натуральных чисел – это наибольшее

Перебор:

k := a; { или k := b; }
while (a mod k <> 0) or
(b mod k <> 0) do
k := k - 1;
writeln ('НОД(', a, ',', b, ')=', k);

много операций для больших чисел

ИЛИ

= НОД(a, b-a)
Заменяем большее из

НОД (14, 21) = НОД (14, 21-14) = НОД (14, 7)

НОД (1998, 2) = НОД (1996, 2) = … = 2

Пример:

много шагов при большой разнице чисел:

= НОД (7, 7) = 7

= НОД(a, b mod a)
Заменяем большее

НОД (14, 21) = НОД (14, 7) = НОД (0, 7) = 7

Пример:

Еще один вариант:

НОД(2·a,2·b)= 2·НОД(a, b)
НОД(2·a,b)= НОД(a, b) // при нечетном b

integer;
begin
if a = b then NOD := a

function NOD (a, b: integer): integer;
begin
if a*b = 0 then NOD := a+b
else
if a < b then
NOD := NOD(a, b mod a)
else NOD := NOD(a mod b, b);
end;

integer;
begin
while a b do
if a

function NOD (a, b: integer): integer;
begin
while a*b <> 0 do
if a > b then a := a mod b
else b := b mod a;
NOD := a + b;
end;

таблицу:


«5»: То же самое, но сравнить для всех пар

делятся только на себя и на 1.
Применение:
криптография;
генераторы псевдослучайных чисел.
Наибольшее

for i:=1 to N do begin
isPrime := True;
for k:=2 to i-1 do
if i mod k = 0 then
isPrime := False;
if isPrime then
writeln(i);
end;

k*k <= i

O(N2)

растет не быстрее N2

версия – решето Аткина .
1 2 3 4 5

Алгоритм:
начать с k = 2;
«выколоть» все числа через k, начиная с 2·k;
перейти к следующему «невыколотому» k;
если k·k <= N, то перейти к шагу 2;
напечатать все числа, оставшиеся «невыколотыми».

высокая скорость, количество операций

нужно хранить в памяти все числа от 1 до N

O((N·log N)·log log N )

2

3

to N do A[i] := True;
{ основной цикл

Логический массив A[N], где A[i] = True, если число i не «выколото», A[i] = False, если число i «выколото».

if A[k] then begin





end;
k := k +

Основной цикл:

i := k*k;
while i <= N do begin
A[i] := False;
i := i + k;
end;

«выкалываем» все числа, кратные k

клавиатуры.
«5»: То же самое, но сравнить число шагов алгоритма

это число содержит более 100 цифр…




Решение: хранить цифры в

100! < 100100

201 цифра

201/6 ≈ 34 ячейки

= 1234·10000002 +
568901·10000001

Хранить число по группам из 6 цифр – это значит представить его в системе счисления с основанием d = 1000000.

[A] = 1;
for k: = 2 to 100 do
[A] = [A]* k;
{ вывести [A] }

Алгоритм:

[A] – длинное число, хранящееся как массив

умножение длинного числа на «короткое»

3

k

a0

a1

a2

c0

c1

c2

734567·3 = 2 203701

c0

перенос, r1

568901·3 + 2 = 1 706705

c1

r2

1234·3 + 1 = 3703

c2

c0 = ( a0·k + 0) mod d
r1 = ( a0·k + 0) / d

c1 = ( a1·k + r1) mod d
r2 = ( a1·k + r1) / d

c2 = ( a2·k + r2) mod d
r3 = ( a2·k + r2) / d
...

}
var A: array[0..40] of integer;
s, r,

{ записать [A]=1 }
A[0] := 1;
for i:=1 to 40

пока не кончились цифры числа [A] или есть перенос

do
write(A[i]);
Проблема: как не потерять первые нули при

write(A[len-1]); { старший разряд }
for i: = len-2 downto 0 do Write6(A[i] );

integer;
begin
x := 100000;
while x > 0 do

= 1·3·...·97·99
«5»: То же самое, но написать свою процедуру

оптимизация

(массив) целых чисел
Комбинаторная оптимизация:
x – вектор (массив) целых чисел,

при малом количестве вариантов можно решить простым перебором

при большом количестве вариантов на решение перебором может потребоваться огромное время (для ряда задач другие алгоритмы неизвестны)

из первого города и, посетив по разу в неизвестном

Точные методы:
простой перебор;
метод ветвей и границ;
метод Литтла;
…
Приближенные методы:
метод случайных перестановок (Matlab);
генетические алгоритмы;
метод муравьиных колоний;
…

большое время счета для больших N

O(N!)

не гарантируется оптимальное решение

задача
1
3
5
2
4
1





Алгоритм:
записать в массив x перестановку 2 3