- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Алгебра логики
Содержание
- 2. Алгебра логики — это математический аппарат, с помощью которого записывают, вычисляют, упрощают и преобразовывают логические высказывания.
- 3. Возникновение логики Понятие логики как науки появилось
- 4. Употребляемые в обычной речи слова и словосочетания
- 5. Логическое высказывание — это любое повествовательное предложение,
- 6. Так, например, из элементарных высказываний “Петров —
- 7. Каждая логическая связка рассматривается как операция над
- 8. (2) Операция, выражаемая связкой “и”, называется конъюнкцией
- 9. (3) Операция, выражаемая связкой “или” (в неразделительном,
- 10. (4) Операция, выражаемая связками “если ..., то”,
- 11. Рассмотрим составное высказывание А В, понимаемое
- 12. (5) Операция, выражаемая связками “тогда и только
- 13. Существуют и другие логические операции:Операция, выражаемая связками
- 14. Любое высказывание можно формализовать, то есть заменить
- 15. Логический элемент компьютера — это часть электронной
- 16. С х е м а ИЕдиница
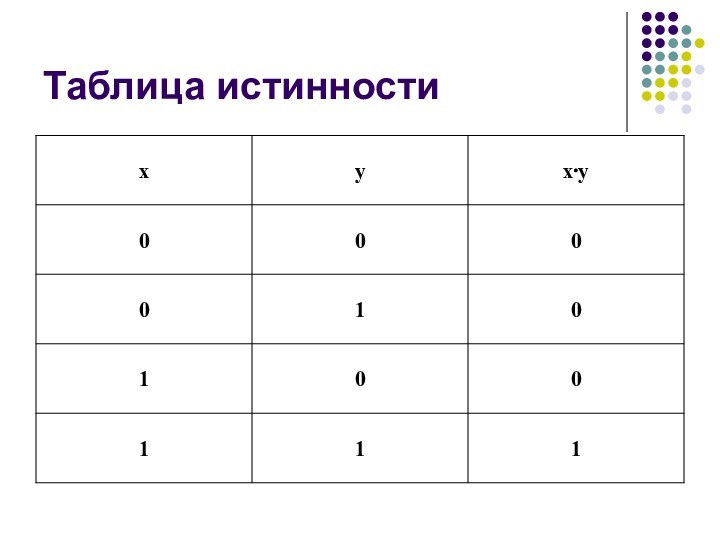
- 17. Таблица истинности
- 18. С х е м а ИЛИСхема
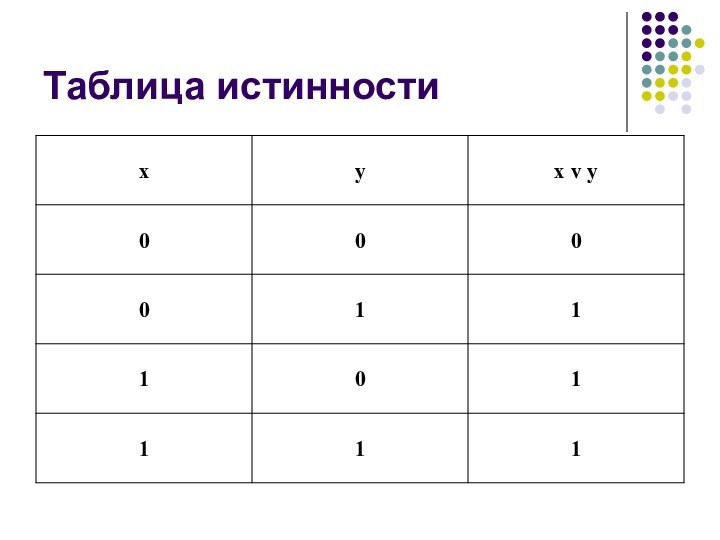
- 19. Таблица истинности
- 20. С х е м а НЕСхема
- 21. Таблица истинности
- 22. С х е м а И
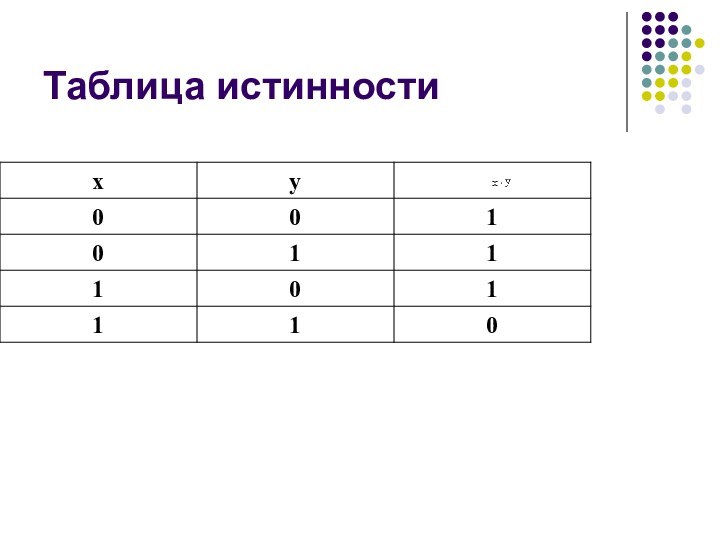
- 23. Таблица истинности
- 24. С х е м а ИЛИ
- 25. Таблица истинности
- 26. Преобразование выражений, состоящих из булевых функцийот перестановки
- 27. Скачать презентацию
- 28. Похожие презентации
Алгебра логики — это математический аппарат, с помощью которого записывают, вычисляют, упрощают и преобразовывают логические высказывания.



















Слайд 2 Алгебра логики — это математический аппарат, с помощью
которого записывают, вычисляют, упрощают и преобразовывают логические высказывания.
Слайд 3
Возникновение логики
Понятие логики как науки появилось ещё
в XIX в., т.е. задолго до появления науки информатики
и компьютеров.Элементы математической логики можно найти уже в работах древнегреческих философов. В XVII в. Г. В. Лейбниц высказал идею о том, что рассуждения могут быть сведены к механическому выполнению определенных действий по установленным правилам.
Однако как самостоятельный раздел математики логика начала формироваться только с середины XIX в..
Слайд 4 Употребляемые в обычной речи слова и словосочетания "не”,
“и”, “или”, “если... , то”, “тогда и только тогда”
и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.Слайд 5 Логическое высказывание — это любое повествовательное предложение, в
отношении которого можно однозначно сказать, истинно оно или ложно. Логические
связки "не”, “и”, “или”, “если... , то”, “тогда и только тогда” и другие позволяют из уже заданных высказываний строить новые высказывания. Высказывания, образованные из других высказываний с помощью логических связок, называются составными. Высказывания, не являющиеся составными, называются элементарными.Слайд 6 Так, например, из элементарных высказываний “Петров — врач”,
“Петров — шахматист” при помощи связки “и” можно получить
составное высказывание “Петров — врач и шахматист”, понимаемое как “Петров — врач, хорошо играющий в шахматы”. При помощи связки “или” из этих же высказываний можно получить составное высказывание “Петров — врач или шахматист”, понимаемое в алгебре логики как “Петров или врач, или шахматист, или и врач и шахматист одновременно”. Истинность или ложность получаемых таким образом составных высказываний зависит от истинности или ложности элементарных высказываний.Слайд 7 Каждая логическая связка рассматривается как операция над логическими
высказываниями и имеет свое название и обозначение: (1) Операция,
выражаемая словом “не”, называется отрицанием и обозначается чертой над высказыванием (или знаком щ ). Высказывание истинно, когда A ложно, и ложно, когда A истинно. Пример. “Луна — спутник Земли” (А); “Луна — не спутник Земли” ( ).Слайд 8 (2) Операция, выражаемая связкой “и”, называется конъюнкцией (лат.
conjunctio — соединение) или логическим умножением и обозначается точкой
"•" (может также обозначаться знаками Щ или &). Высказывание А•В истинно тогда и только тогда, когда оба высказывания А и В истинны. Например, высказывание “10 делится на 2 и 5 больше 3” истинно, а высказывания “10 делится на 2 и 5 не больше 3”, “10 не делится на 2 и 5 больше 3”, “10 не делится на 2 и 5 не больше 3” ложны.Слайд 9 (3) Операция, выражаемая связкой “или” (в неразделительном, неисключающем
смысле этого слова), называется дизъюнкцией (лат. disjunctio — разделение)
или логическим сложением и обозначается знаком v (или плюсом). Высказывание А v В ложно тогда и только тогда, когда оба высказывания А и В ложны. Например, высказывание “10 не делится на 2 или 5 не больше 3” ложно, а высказывания “10 делится на 2 или 5 больше 3”, “10 делится на 2 или 5 не больше 3”, “10 не делится на 2 или 5 больше 3” истинны.Слайд 10 (4) Операция, выражаемая связками “если ..., то”, “из
... следует”, “... влечет ...”, называется импликацией (лат. implico
— тесно связаны) и обозначается знаком . Высказывание А В ложно тогда и только тогда, когда А истинно, а В — ложно. Например, даны 2 высказывания: “данный четырёхугольник — квадрат” (А) и “около данного четырёхугольника можно описать окружность” (В).Слайд 11 Рассмотрим составное высказывание А В, понимаемое как
“если данный четырёхугольник квадрат, то около него можно описать
окружность”. Есть три варианта, когда высказывание А В истинно:А истинно и В истинно, то есть данный четырёхугольник квадрат, и около него можно описать окружность;
А ложно и В истинно, то есть данный четырёхугольник не является квадратом, но около него можно описать окружность (разумеется, это справедливо не для всякого четырёхугольника);
A ложно и B ложно, то есть данный четырёхугольник не является квадратом, и около него нельзя описать окружность.
Ложен только один вариант: А истинно и В ложно, то есть данный четырёхугольник является квадратом, но около него нельзя описать окружность.
Слайд 12 (5) Операция, выражаемая связками “тогда и только тогда”,
"необходимо и достаточно”, “... равносильно ...”, называется эквиваленцией или
двойной импликацией и обозначается знаком или ~ . Высказывание А В истинно тогда и только тогда, когда значения А и В совпадают.
Слайд 13
Существуют и другие логические операции:
Операция, выражаемая связками “если
..., то”, “из ... следует”, “... влечет ...”, называется
импликацией.Операция, выражаемая связками “тогда и только тогда”, "необходимо и достаточно”, “... равносильно ...”, называется эквиваленцией или двойной импликацией.
Импликацию можно выразить через дизъюнкцию и отрицание.
Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию.
Слайд 14 Любое высказывание можно формализовать, то есть заменить логической
формулой. Формулы, принимающие значение “истина” при любых значениях истинности входящих
в них переменных называются тождественно истинными формулами или тавтологиями. Формулы, принимающие значение “ложно” при любых значениях истинности входящих в них переменных , называются тождественно ложными формулами или противоречиями. Две формулы при одинаковых наборах значений входящих в них переменных, принимающие одинаковые значения, называются равносильными.Слайд 15 Логический элемент компьютера — это часть электронной логичеcкой
схемы, которая реализует элементарную логическую функцию. Таблица истинности это
табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.
Слайд 16
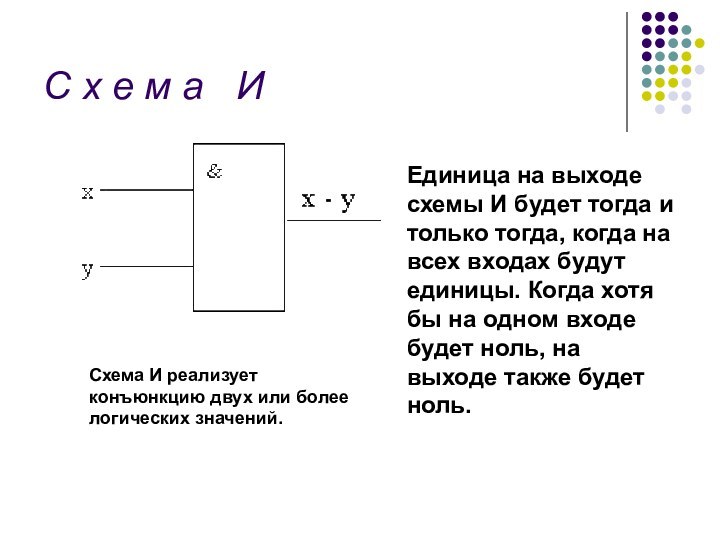
С х е м а И
Единица на
выходе схемы И будет тогда и только тогда, когда
на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль.Схема И реализует конъюнкцию двух или более логических значений.
Слайд 18
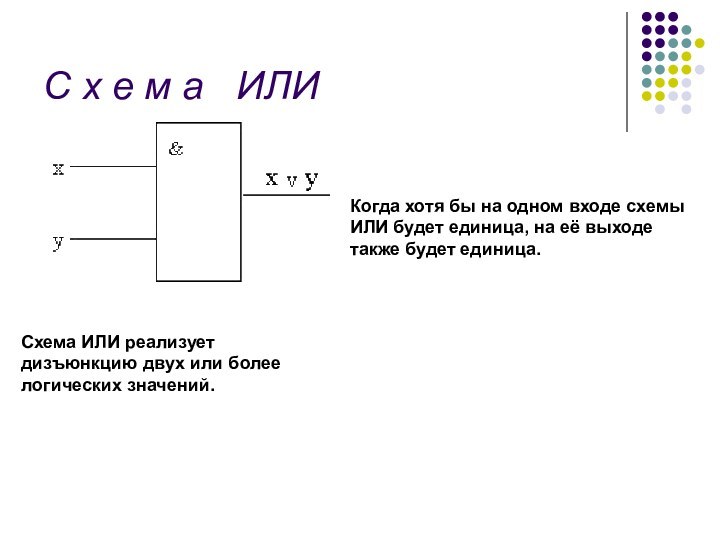
С х е м а ИЛИ
Схема ИЛИ
реализует дизъюнкцию двух или более логических значений.
Когда хотя
бы на одном входе схемы ИЛИ будет единица, на её выходе также будет единица.
Слайд 20
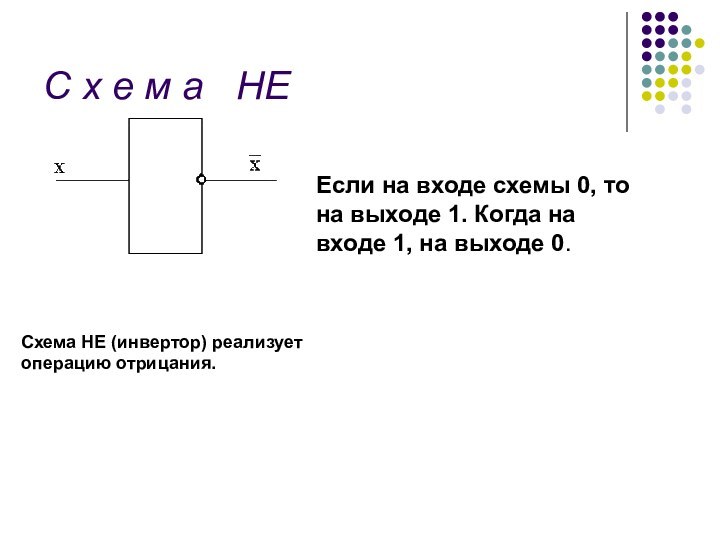
С х е м а НЕ
Схема НЕ
(инвертор) реализует операцию отрицания.
Если на входе схемы 0,
то на выходе 1. Когда на входе 1, на выходе 0. Слайд 22 С х е м а И -
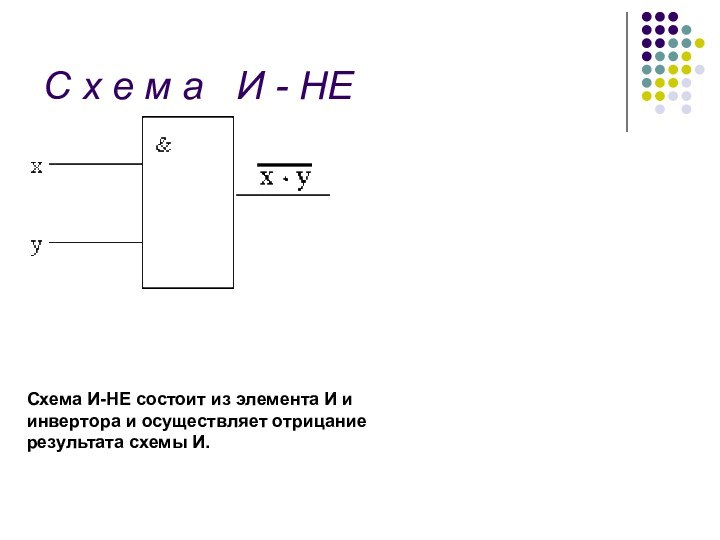
НЕ
Схема И-НЕ состоит из элемента И и инвертора и
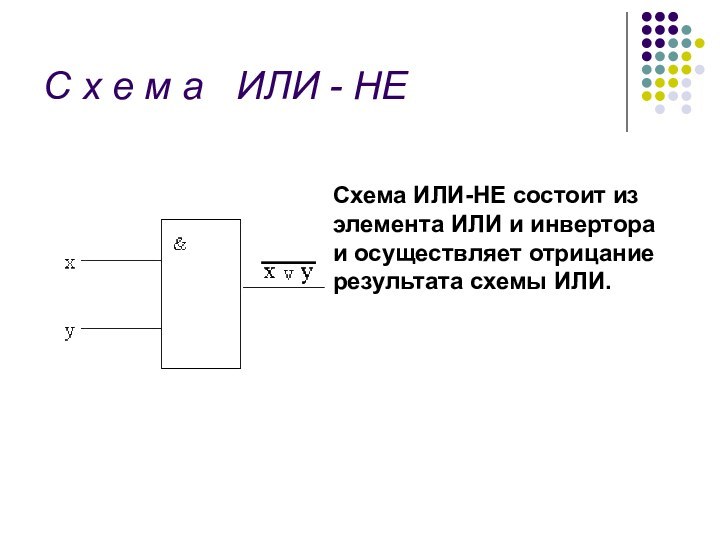
осуществляет отрицание результата схемы И.Слайд 24 С х е м а ИЛИ -
НЕ
Схема ИЛИ-НЕ состоит из элемента ИЛИ и инвертора и
осуществляет отрицание результата схемы ИЛИ.
Слайд 26
Преобразование выражений, состоящих из булевых функций
от перестановки мест
аргументов результат не изменяется
A & B = B &
Aсуществует следующий закон
A & (B & C) = (A & B) & C
Также существуют некоторые тождества, опирающиеся на особые свойства функции, например:
1) A & (~A) = ЛОЖЬ
2) (~A) & (~B) = ~ (A v B)
Аналогично, сложение и логическое «ИЛИ»:
от перестановки мест аргументов результат не изменяется
A v B = B v A
существует следующий закон
(A v B) v С = A v (B v C)
можно выносить общий множитель за скобки
(A & B) v (С & B) = B & (A v C)
И также некоторые собственные законы:
1) A v (~A) = ИСТИНА
2) (~A) v (~B) = ~ (A & B)