- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Алгебра логики (3)
Содержание
- 2. Логика - это наука о формах и способах мышления. Понятие; Высказывание; Умозаключение Основные формы мышления:
- 3. это форма мышления, фиксирующая основные, существенные признаки объекта.Понятие - СодержаниеОбъем
- 4. Высказывание может быть истинно или ложно.Высказывание -
- 5. Посылками умозаключения по правилам формальной логики могут
- 6. В алгебре высказываний высказывания обозначаются именами логических
- 7. Для образования новых высказываний используются базовые логические
- 8. Логическое отрицание -операция не - инверсияНЕАА
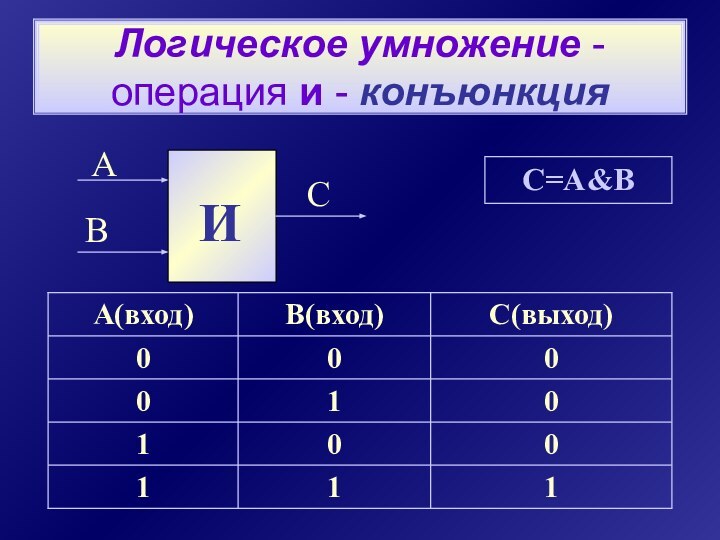
- 9. Логическое умножение - операция и - конъюнкцияC=A&B
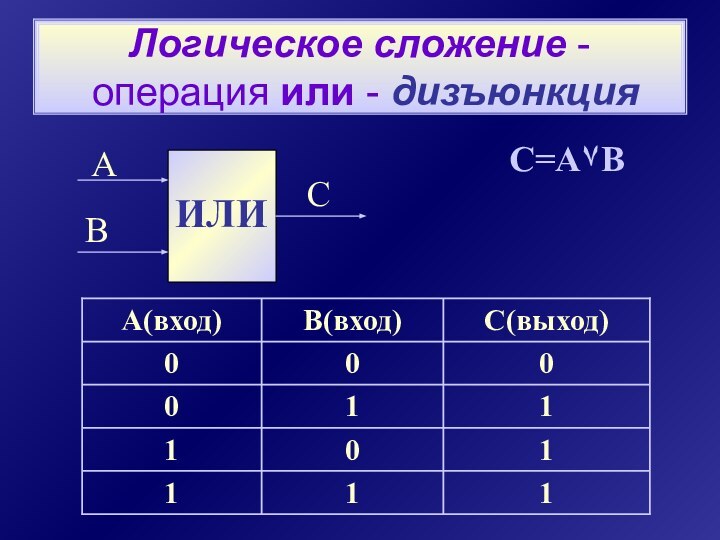
- 10. Логическое сложение - операция или - дизъюнкцияИЛИАВСC=A۷B
- 11. Каждое составное высказывание можно выразить в виде
- 12. Логические законы и правила преобразования логических выраженийЗакон
- 13. Логические законы и правила преобразования логических выраженийЗаконы
- 14. Таблицы истинностиКоличество строк = 2 ª, где
- 15. Скачать презентацию
- 16. Похожие презентации
Логика - это наука о формах и способах мышления. Понятие; Высказывание; Умозаключение Основные формы мышления:













Слайд 3
это форма мышления, фиксирующая основные, существенные признаки объекта.
Понятие
-
Содержание
Объем
Слайд 4
Высказывание может быть истинно или ложно.
Высказывание -
это
форма мышления, в которой что-либо утверждается или отрицается о
реальных предметах, их свойствах и отношениях между ними.Слайд 5 Посылками умозаключения по правилам формальной логики могут быть
только истинные суждения.
Умозаключение -
это форма мышления, с помощью
которой из одного или несколько суждений (посылок) может быть получено новое суждение (заключение).Слайд 6 В алгебре высказываний высказывания обозначаются именами логических переменных,
которые могут принимать лишь два значения «истинно» и «ложно».
Истинно =1
Ложно=0
Алгебра
высказываний
Слайд 7
Для образования новых высказываний используются базовые логические операции:
инверсия
логическое
отрицание
операция не
конъюнкция
дизъюнкция
логическое умножение
операция и
логическое сложение
операция или
Слайд 11 Каждое составное высказывание можно выразить в виде формулы
(логического выражения), в которую входят логические переменные, обозначающие высказывания,
и знаки логических операций, обозначающие логические функции.Логические
выражения
Слайд 12
Логические законы и правила преобразования логических выражений
Закон тождества:
всякое высказывание тождественно самому себе.
А=А
Закон непротиворечия: высказывание не
может быть одновременно истинным и ложным.А & А=1
Закон исключенного третьего. Высказывание может быть истинным, либо ложным, третьего не дано.
А ۷ А=1
Закон двойного отрицания: если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание.
А=А