- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Алгоритмическое обеспечение информатики
Содержание
- 2. ПОНЯТИЕ АЛГОРИТМА Слово «алгоритм» происходит от имени великого
- 3. Алгоритм – это система однозначных инструкций (указаний),
- 4. АЛГОРИТМЫ:численные;логические.Численные алгоритмы – это алгоритмы, в соответствии
- 5. Дискретность – последовательное выполнение простых или ранее определённых
- 6. К основным способам описания алгоритмов можно отнести
- 7. СЛОВЕСНО-ФОРМУЛЬНЫЙ СПОСОБПри словесно-формульном способе алгоритм записывается в виде текста
- 8. При графическом представлении алгоритм изображается в виде
- 10. Псевдокод представляет собой систему обозначений и правил, предназначенную
- 11. ДИАГРАММА НЭССИ-ШНЕЙДЕРМАНА
- 12. ПРОГРАММНЫЙ СПОСОБ
- 13. БАЗОВЫЕ АЛГОРИТМИЧЕСКИЕ СТРУКТУРЫЛогическая структура любого алгоритма может
- 14. 2. Базовая структура "ветвление". Обеспечивает в зависимости
- 16. 3. Базовая структура "цикл". Обеспечивает многократное выполнение некоторой совокупности
- 17. ПРЕДСТАВЛЕНИЕ И ОБРАБОТКА ДАННЫХАлгоритм, реализующий решений некоторой
- 18. Тип данных – это характеристика данных, определяющая
- 19. Целочисленные типы - обозначают множества целых чисел в
- 20. Логический тип (Boolean) - состоит всего из двух
- 21. Символьный тип (Char) - это тип данных, состоящих
- 22. Строковый тип (String, String[n]) - этот тип данных
- 23. Вещественные типы - обозначают множества вещественных чисел в
- 24. Массив (array). Он представляет собой заранее известное
- 25. Представление и обработка данных в виде деревьевЭлементы
- 26. Скачать презентацию
- 27. Похожие презентации












![Алгоритмическое обеспечение информатики Строковый тип (String, String[n]) - этот тип данных определяет последовательности символов - строки.](/img/tmb/15/1467239/dae79a12c59a91f1319f3ec2f1f705c6-720x.jpg)


Слайд 2
ПОНЯТИЕ АЛГОРИТМА
Слово «алгоритм» происходит от имени великого среднеазиатского
ученого 8–9 вв. Аль-Хорезми.
дошли только две – алгебраическая и арифметическая. Вторая книга долгое время считалась потерянной, но в 1857 в библиотеке Кембриджского университета был найден ее перевод на латинский язык. В ней описаны четыре правила арифметических действий, практически те же, что используются и сейчас. Первые строки этой книги были переведены так: «Сказал Алгоритми. Воздадим должную хвалу Богу, нашему вождю и защитнику». Так имя Аль-Хорезми перешло в «Алгоритми», откуда и появилось слово «алгоритм».Слайд 3 Алгоритм – это система однозначных инструкций (указаний), которая
определяет последовательность действий над выбранными объектами с целью получения
результата за конечное число шагов.Алгоритм – это заданное на некотором языке конечное предписание, задающее конечную последовательность выполнимых и точно определенных элементарных операций для решения задачи.
Алгоритм (по Колмогорову) – это система вычислений, выполняемых по строго определенным правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи.
Алгоритм (по Маркову) – это точное предписание, определяющее вычислительный процесс, идущий от варьируемых исходных данных к искомому результату.
Слайд 4
АЛГОРИТМЫ:
численные;
логические.
Численные алгоритмы – это алгоритмы, в соответствии с
которыми решение задач сводится к арифметическим действиям.
Логические алгоритмы –
это алгоритмы, в соответствии с которыми решение задач сводится к логическим действиям.Требования к алгоритмам:
Содержать конечное количество элементарно выполнимых предписаний, т.е. удовлетворять требованию конечности записи;
Выполнять конечное количество шагов при решении задачи, т.е. удовлетворять требованию конечности действий;
Быть единым для всех допустимых исходных данных, т.е. удовлетворять требованию универсальности;
Приводить к правильному по отношению к поставленной задаче решению, т.е. удовлетворять требованию правильности.
Слайд 5
Дискретность – последовательное выполнение простых или ранее определённых (подпрограммы)
шагов. Преобразование исходных данных в результат осуществляется дискретно во
времени.Определенность состоит в совпадении получаемых результатов независимо от пользователя и применяемых технических средств (однозначность толкования инструкций).
Результативность означает возможность получения результата после выполнения конечного количества операций.
Массовость заключается в возможности применения алгоритма к целому классу однотипных задач, различающихся конкретными значениями исходных данных (разработка в общем виде).
Для задания алгоритма необходимо описать следующие его элементы:
набор объектов, составляющих совокупность возможных исходных данных, промежуточных и конечных результатов;
правило начала;
правило непосредственной переработки информации (описание последовательности действий);
правило окончания;
правило извлечения результатов.
СВОЙСТВА АЛГОРИТМА
Слайд 6
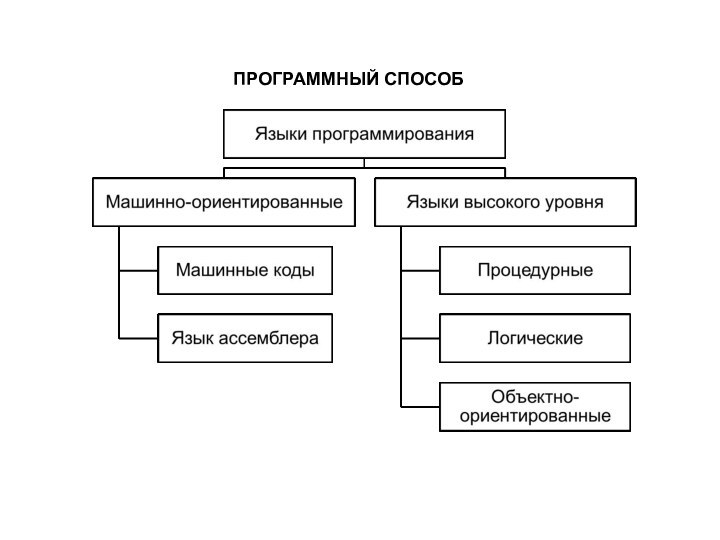
К основным способам описания алгоритмов можно отнести следующие:
словесно-формульный
(на естественном языке);
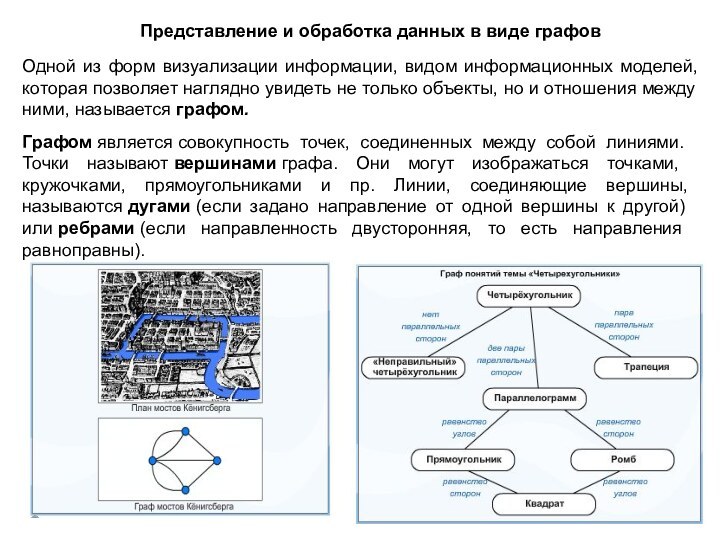
с помощью граф-схем (граф - совокупность точек
и линий, в которой каждая линия соединяет две точки. Точки называются вершинами, линии - рёбрами);псевдокод;
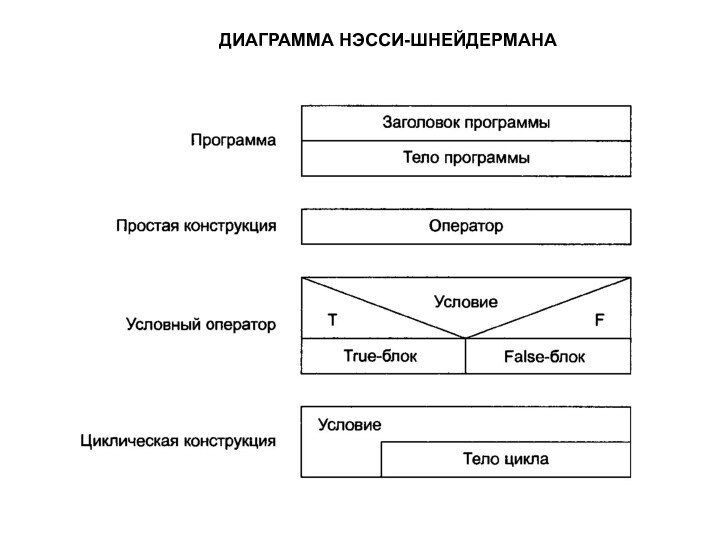
с помощью диаграмм Нэсси-Шнейдермана;
программный.
СПОСОБЫ ОПИСАНИЯ АЛГОРИТМОВ
Слайд 7
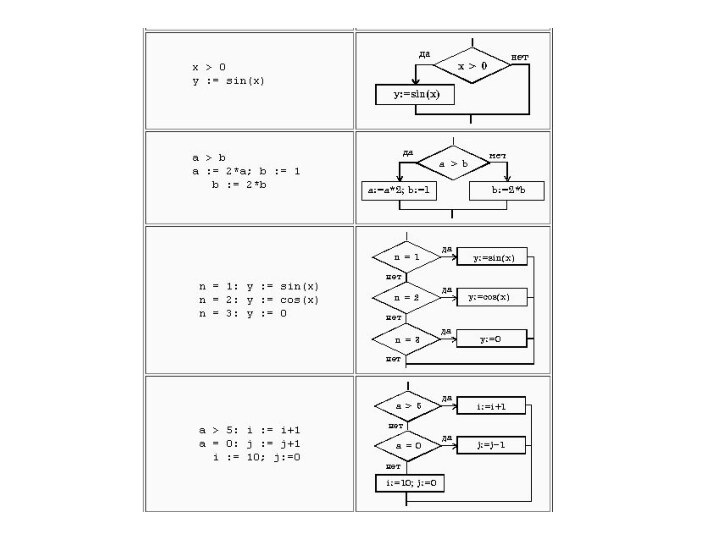
СЛОВЕСНО-ФОРМУЛЬНЫЙ СПОСОБ
При словесно-формульном способе алгоритм записывается в виде текста с
формулами по пунктам, определяющим последовательность действий.
Пусть, например, необходимо найти
значение следующего выражения:у=2а-(х+6).
Словесно-формульным способом алгоритм решения этой задачи может быть записан в следующем виде:
1.Ввести значения а и х.
2.Сложить х и 6.
3.Умножить а на 2.
4.Вычесть из 2а сумму (х+6).
5.Вывести у как результат вычисления выражения.
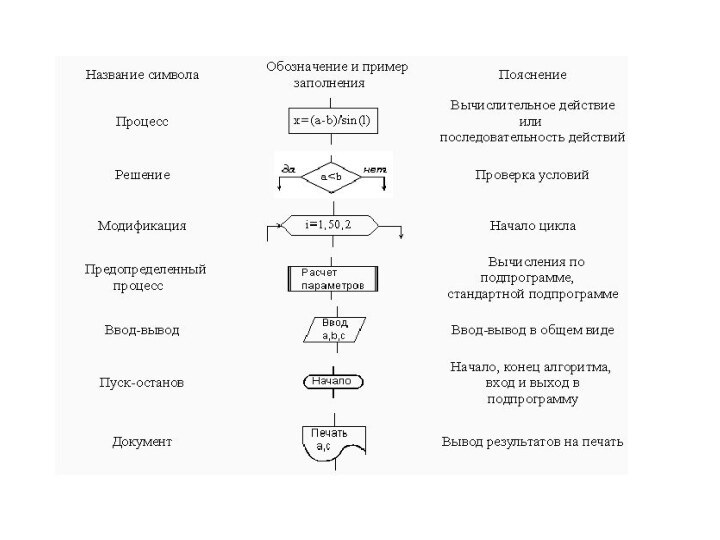
Слайд 8 При графическом представлении алгоритм изображается в виде последовательности связанных
между собой функциональных блоков, каждый из которых соответствует выполнению одного
или нескольких действий.ГРАФИЧЕСКИЙ СПОСОБ
Такое графическое представление называется схемой алгоритма или блок-схемой. В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий.
Слайд 10 Псевдокод представляет собой систему обозначений и правил, предназначенную для
единообразной записи алгоритмов.
ПСЕВДОКОД
Для записи предложений используются: русский язык,
формальные языки предметных областей, в которых решается исходная задача; ключевые слова псевдокодов.Для реализации псевдокодов, в них резервируются следующие ключевые слова:
АЛГОРИТМ,
НАЧАЛО_алгоритма,
КОНЕЦ_алгоритма,
ПОДАЛГОРИТМ,
НАЧАЛО_вспомогательного алгоритма,
КОНЕЦ_вспомогательного алгоритма,
НАЧАЛО_описания переменных,
КОНЕЦ_описания переменных,
НАЧАЛО_если <условие>,
ТО,
ИНАЧЕ,
КОНЕЦ_если,
НАЧАЛО_цикла с предусловием <условие входа в цикл>,
КОНЕЦ_цикла с предусловием,
НАЧАЛО_цикла с постусловием,
КОНЕЦ_цикла с постусловием <условие выхода из цикла>,
НАЧАЛО_цикла с параметром <параметр, его диапазон и шаг>,
КОНЕЦ_цикла с параметром <параметр цикла>.
Слайд 13
БАЗОВЫЕ АЛГОРИТМИЧЕСКИЕ СТРУКТУРЫ
Логическая структура любого алгоритма может быть
представлена комбинацией трех базовых структур: следование, ветвление, цикл.
1. Базовая структура "следование".
Образуется последовательностью действий, следующих одно за другим:
Слайд 14
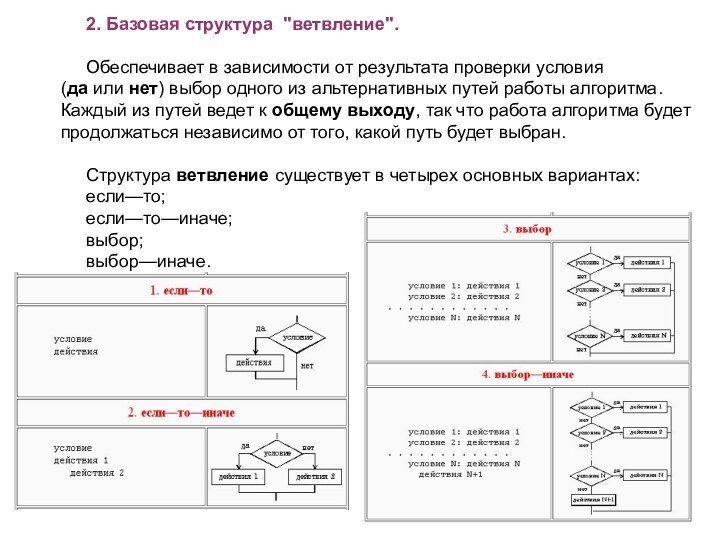
2. Базовая структура "ветвление".
Обеспечивает в зависимости от
результата проверки условия (да или нет) выбор одного из альтернативных путей
работы алгоритма. Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран.Структура ветвление существует в четырех основных вариантах:
если—то;
если—то—иначе;
выбор;
выбор—иначе.
Слайд 16
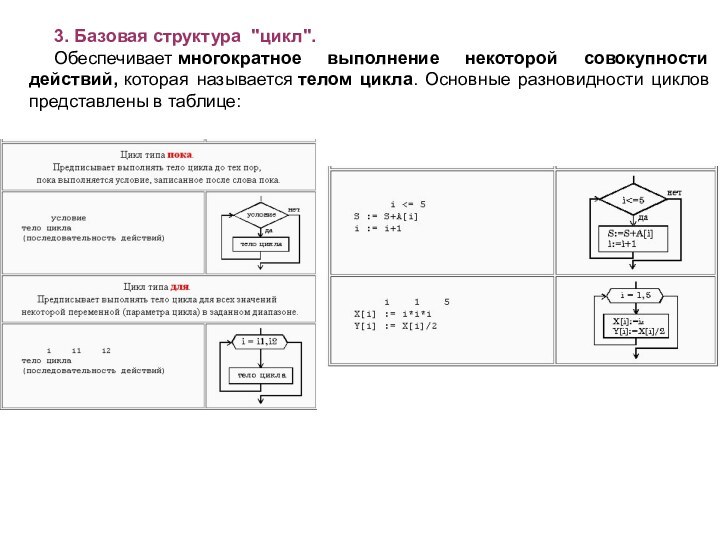
3. Базовая структура "цикл".
Обеспечивает многократное выполнение некоторой совокупности действий, которая
называется телом цикла. Основные разновидности циклов представлены в таблице:
Слайд 17
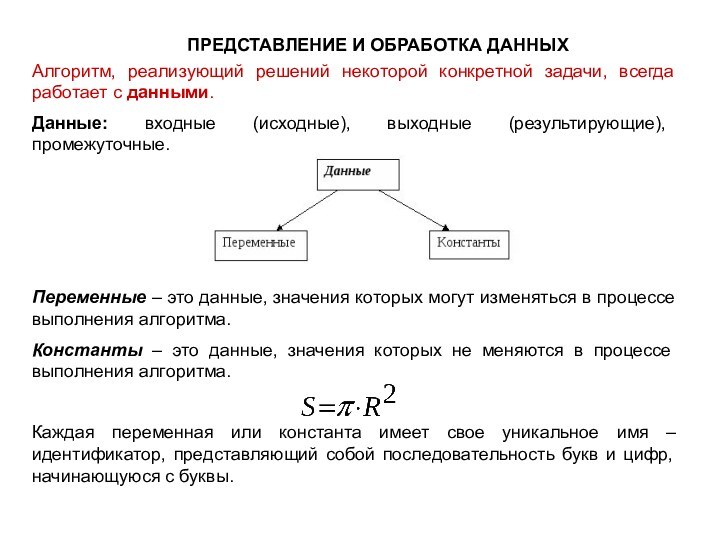
ПРЕДСТАВЛЕНИЕ И ОБРАБОТКА ДАННЫХ
Алгоритм, реализующий решений некоторой конкретной
задачи, всегда работает с данными.
Данные: входные (исходные), выходные (результирующие),
промежуточные.Переменные – это данные, значения которых могут изменяться в процессе выполнения алгоритма.
Константы – это данные, значения которых не меняются в процессе выполнения алгоритма.
Каждая переменная или константа имеет свое уникальное имя – идентификатор, представляющий собой последовательность букв и цифр, начинающуюся с буквы.
Слайд 18
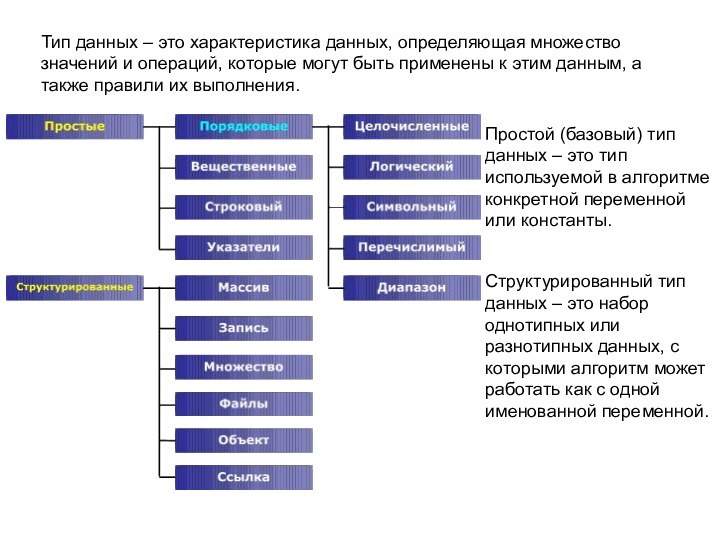
Тип данных – это характеристика данных, определяющая множество
значений и операций, которые могут быть применены к этим
данным, а также правили их выполнения.Простой (базовый) тип данных – это тип используемой в алгоритме конкретной переменной или константы.
Структурированный тип данных – это набор однотипных или разнотипных данных, с которыми алгоритм может работать как с одной именованной переменной.
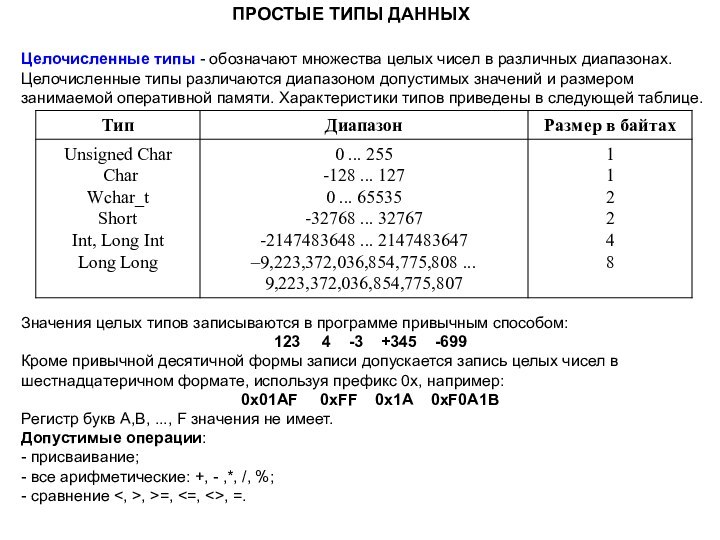
Слайд 19 Целочисленные типы - обозначают множества целых чисел в различных
диапазонах. Целочисленные типы различаются диапазоном допустимых значений и размером
занимаемой оперативной памяти. Характеристики типов приведены в следующей таблице.Значения целых типов записываются в программе привычным способом:
123 4 -3 +345 -699
Кроме привычной десятичной формы записи допускается запись целых чисел в шестнадцатеричном формате, используя префикс 0x, например:
0x01AF 0xFF 0x1A 0xF0A1B
Регистр букв A,B, ..., F значения не имеет.
Допустимые операции:
- присваивание;
- все арифметические: +, - ,*, /, %;
- сравнение <, >, >=, <=, <>, =.
ПРОСТЫЕ ТИПЫ ДАННЫХ
Слайд 20
Логический тип (Boolean) - состоит всего из двух значений:
False (ложно)
и True (истинно).
Слова False и True определены в языке и являются, по сути, логическими
константами. Регистр букв в их написании несущественен: FALSE = false. Значения этого типа являются результатом вычислений условных и логических выражений и участвуют во всевозможных условных операторах языка.Допустимые операции: - присваивание; - сравнение: <, >, >=, <=, <>, =; - логические операции: NOT (!), OR (||), AND(&&)
Слайд 21 Символьный тип (Char) - это тип данных, состоящих из
одного символа (знака, буквы, кода). Значением типа Char может
быть любой символ из набора ASCII. Если символ имеет графическое представление, то в программе он записывается заключенным в одиночные кавычки (апострофы), например:'ж' 's' '.' '*' ' '-(пробел)
Для представления самого апострофа используется префикс \'. Если же символ не имеет графического представления, например, символ табуляции или символ возврата каретки, то можно воспользоваться эквивалентной формой записи символьного значения, состоящего из префикса \х и ASCII-кода символа в шестнадцатеричной кодировке:
\x009 (\t) \x00A (\n) \x020
Допустимые операции: - присваивание; - сравнение: <, >, >=, <=, <>, =. Большим считается тот символ, который имеет больший ASCII-номер.
Слайд 22 Строковый тип (String, String[n]) - этот тип данных определяет
последовательности символов - строки. Параметр n определяет максимальное количество
символов в строке. Если он не задан, подразумевается n=255. Значение типа "строка" в программе записывается как последовательность символов, заключенных в одиночные кавычки (апострофы), например'Это текстовая строка' 'This is a string' '1234' - это тоже строка, не число '' - пустая строка
Допустимые операции: - присваивание; - сложение (конкатенация, слияние); например, S := 'Зима'+' '+'пришла!'; - сравнение: <, >, >=, <=, <>, =.
Строки считаются равными, если имеют одинаковую длину и посимвольно эквивалентны.
Слайд 23 Вещественные типы - обозначают множества вещественных чисел в различных
диапазонах. Вещественные типы различаютхся диапазоном допустимых значений и размером
занимаемой оперативной памяти. Вещественные типы и их характеристики приведены в следующей таблице.Допустимые операции:
- присваивание;
- все арифметические: +, - ,*, / ;
- сравнение: <, >, >=, <=, <>, =.
Слайд 24 Массив (array). Он представляет собой заранее известное количество
однотипных элементов, снабженных индексами. Массив может быть одномерным или
многомерным.Запись (record). Она включает в себя несколько полей, тип которых может отличаться друг от друга. Например, товар на складе описывается следующими величинами: наименование, количество, цена, наличие сертификата качества и т.д. В этом примере наименование – величина типа string, количество – integer, цена – real, наличие сертификата – boolean.
Запись представляет собой наиболее общий и гибкий структурированный тип данных, так как она может быть образована из неоднотипных компонентов и в ней явным образом выражена связь между элементами данных, характеризующими реальный объект.
Строка (string) – последовательность символов кодовой таблицы персонального компьютера. Количество символов в строке может изменяться от 0 до 255.
Множество (set) – это набор взаимосвязанных по какому-либо признаку или группе признаков элементов. Каждый элемент во множестве называется элементом множества. Множество должно состоять из порядковых элементов, и их число не должно превышать 255.
Файл (file) – последовательность однотипных компонентов, записанных на внешнем носителе под определенным именем. Тип этих компонентов может быть любой, за исключением типа – файла. Размер файла не объявляется.
СТРУКТУРИРОВАННЫЕ ТИПЫ ДАННЫХ
Слайд 25
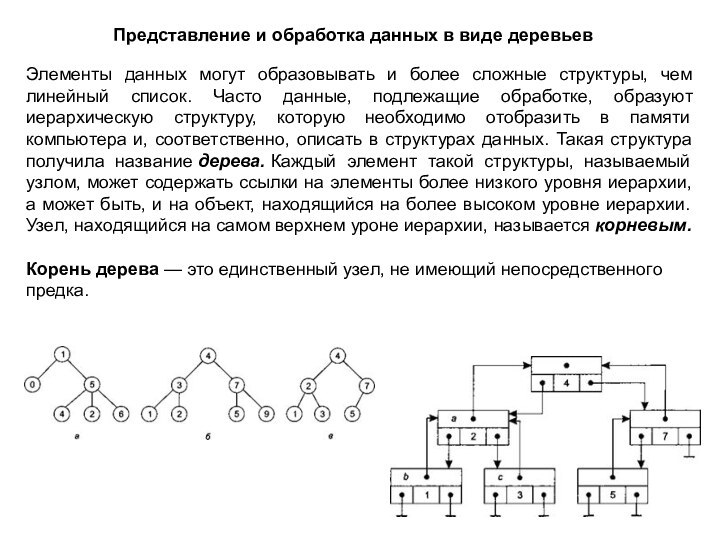
Представление и обработка данных в виде деревьев
Элементы данных
могут образовывать и более сложные структуры, чем линейный список.
Часто данные, подлежащие обработке, образуют иерархическую структуру, которую необходимо отобразить в памяти компьютера и, соответственно, описать в структурах данных. Такая структура получила название дерева. Каждый элемент такой структуры, называемый узлом, может содержать ссылки на элементы более низкого уровня иерархии, а может быть, и на объект, находящийся на более высоком уровне иерархии. Узел, находящийся на самом верхнем уроне иерархии, называется корневым.Корень дерева — это единственный узел, не имеющий непосредственного предка.