Презентация на тему Арифметические основы работы ЭВМ

.

. . . .
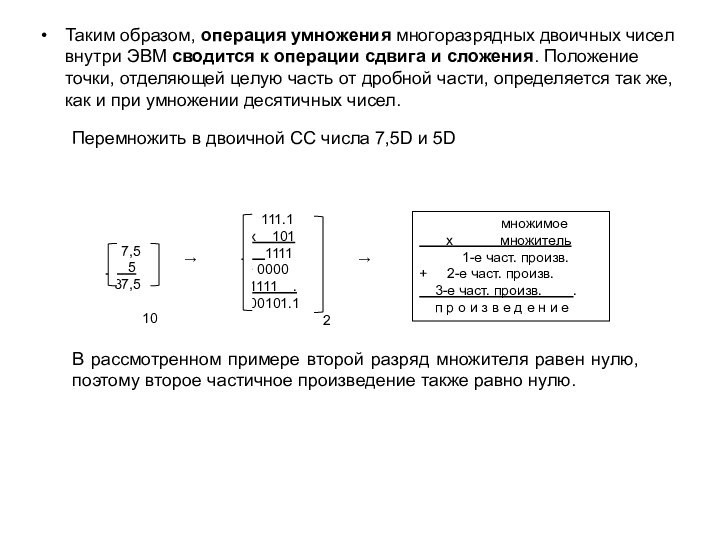
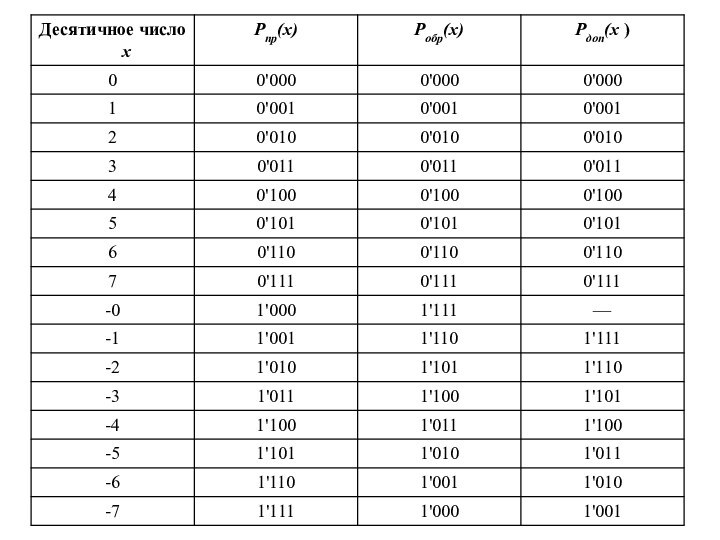
13 01101
+ 7 → + 00111
20 10100

В устройствах, реализующих операцию арифметического сложения двоичных чисел, операнды представляют числами определенной разрядности (одинаковой для обоих операндов). При этом неиспользуемые старшие разряды заполняются нулями. Также заполняются нулями младшие разряды дробной части вещественного числа (справа от точки).
Следует заметить, что в реальных ЭВМ чаще всего используются 16-, 32-, 64-разрядные сетки (машинные слова). Однако для учебных целей при рассмотрении методов выполнения арифметических операций не будем обращать внимание на разрядность операндов (т. е. будем использовать разрядность, отличающуюся от разрядности реальных ЭВМ).

двоичной системе счисления.
При сложении вещественных чисел в общем случае

перенос осуществляется и из дробной части числа в целую часть.

Рассмотрим правило умножения многоразрядных двоичных чисел

Умножение двоичных многоразрядных чисел производится путем образования частичных произведений и последующего их суммирования. Каждое частичное произведение равно нулю, если в соответствующем разряде множителя стоит 0, или равно множимому, сдвинутому на соответствующее число разрядов влево, если в разряде множителя стоит 1.

ЭВМ сводится к операции сдвига и сложения. Положение точки,

отделяющей целую часть от дробной части, определяется так же, как и при умножении десятичных чисел.

Перемножить в двоичной СС числа 7,5D и 5D

В рассмотренном примере второй разряд множителя равен нулю, поэтому второе частичное произведение также равно нулю.

применяют специальные коды. За счет этого облегчается определение знака

результата операции, а операция вычитания чисел сводится к арифметическому сложению. В результате упрощаются устройства, выполняющие арифметические операции.
В ВТ применяют прямой, обратный и дополнительный коды.
Прямой двоичный код Рпр(х) — это такое представление двоичного числа х, при котором знак «+» кодируется нулем в старшем разряде числа, а знак «–» — единицей. При этом старший разряд называется знаковым.
Например, числа +5D и –5D, представленные в прямом четырехразрядном коде, выглядят так: +5D = 0'101B; –5D = 1'101B. Здесь апострофом условно (для удобства определения знака) отделены знаковые разряды.
0' Pпр(х), при х ≥ 0
Робр(х) =
1' Pпр(х), при х ≤ 0.
Обратный код Робр(х) получается из прямого кода по следующему правилу:

0' Pпр(х), при х ≥ 0
Робр(х) =
1' Pпр(х), при х ≤ 0.

положительных чисел совпадает с прямым кодом. Чтобы представить отрицательное

двоичное число в обратном коде, нужно поставить в знаковом разряде 1, во всех значащих разрядах заменить 1 на 0, а 0 на 1. Такая операция называется инверсией и обозначается горизонтальной чертой над инвертируемым выражением (см. разд. «Логические основы работы ЭВМ»).
Получить обратный код для числа х = –11D.

Рпр(х) = (1'1011)2
Робр(х) = (1'0100)2.
Считается, что здесь числа представлены пятью разрядами. Из рассмотренного примера видно, что обратный код для положительных чисел совпадает с прямым, а для отрицательных чисел получается инверсией (переворотом) всех разрядов, кроме знакового разряда.

Дополнительный код Рдоп(х ) образуется следующим образом

совпадает с прямым кодом, а для отрицательного числа получается

инверсией всех значащих разрядов и добавлением единицы к младшему разряду результата.
Дополнительный код отрицательного числа может быть получен из обратного кода путем прибавления 1 к младшему разряду обратного кода (естественно, с учетом переносов между разрядами).

0' Pпр(х), при х ≥ 0
Рдоп(х) =
1' Pпр(х) + 1, при х < 0.

Получить дополнительный код для числа х = –13D.
Решение.
Рпр(х) = ( 1'1101 )2 прямой код
Робр(х) = ( 1'0010 )2 обратный код
Рдоп(х ) = ( 1'0011)2  дополнительный код.
В табл. представлены прямые, обратные и дополнительные коды чисел от –7D до +7D.

алгебраическом сложении двоичных чисел положительные слагаемые представляют в прямом

коде, а отрицательные числа (слагаемые) — в дополнительном коде и производят арифметическое суммирование этих кодов, включая разряды знаков, которые при этом рассматривают как старшие разряды. При возникновении переноса из разряда знака единицу переноса отбрасывают. В результате получают алгебраическую сумму в прямом коде, если эта сумма положительная, и в дополнительном коде, — если сумма отрицательная.
Напомним, что алгебраическое сложение — это сложение, в котором могут участвовать как положительные, так и отрицательные числа.

чисел х1 = 7D и х2 = –3D.
Решение.
Необходимо найти

сумму: y = x1 + x2.
Учитывая, что x1 > 0, это число нужно представить в прямом коде, а так как x2 < 0, то x2 нужно перевести в дополнительный код. . . .
0'111
P(y) = + 1'101
0'100
2
P(y) = Рпр(x1) + Рдоп(x2).
Рпр(x1) = 0'111В
Рпр(x2) = 1'011B
Робр(х2) = 1'100B
Рдоп(x2) = 1'101B.
Так как результат положителен (в знаковом разряде P(y) — 0), значит, он представлен в прямом коде. После перевода двоичного числа в десятичную СС получим ответ: y = +4D.