Презентация на тему Деревья - структуры данных

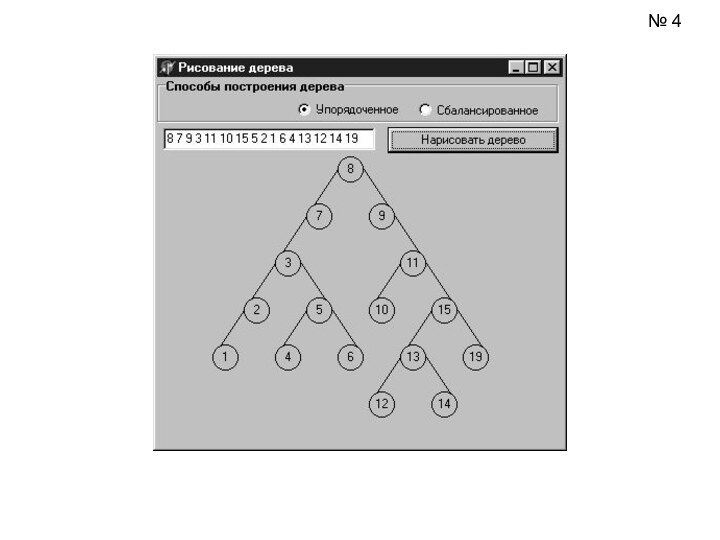
структура (дерево) определяется следующим образом: дерево (tree) с базовым

типом T — это:
либо пустая структура;
либо узел типа T, с которым связано конечное число древовидных структур, называемых поддеревьями (subtree).

Если с узлом связаны только два поддерева, то дерево называется бинарным.

№

где может возникнуть ветвь.
корень (root) — "верхний" узел дерева.;
ветвь

(brunch) — отрезок, описывающий связь между двумя узлами;
лист (leaf) — узел, из которого не выходят ветви, т. е. не имеющий поддеревьев.

№

Терминология (1)

узел, который находится непосредственно над другим узлом;
дочерним (child) называется

узел, который находится непосредственно под другим узлом; дочерний узел также называют сыном (что не меняет "родственности" отношений);
предки данного узла — это все узлы на пути вверх от данного узла до корня;
потомки — все узлы, расположенные ниже данного;
сестринские (братские) — узлы, у которых один и тот же родитель.

№

Терминология (2)

узел, не являющийся листом;
порядок узла (node degree) — количество его

дочерних узлов;
глубина (depth) узла — количество его предков плюс единица;
глубина (высота) дерева — максимальная глубина всех узлов;
длина пути к узлу — количество ветвей, которые нужно пройти, чтобы продвинуться от корня к данному узлу;
длина пути дерева — сумма длин путей всех его узлов. Она также называется длиной внутреннего пути.

№

Терминология (3)

удаляются узлы, меняются информационные части узлов. То есть дерево

является динамической структурой.
Поэтому узел дерева определяется как переменная с фиксированной структурой, содержащей информационную часть и две ссылки, указывающие на левое и правое поддеревья данного узла.
Ссылка на пустое дерево равна null.

№

Основные операции с бинарными деревьями

получить доступ к каждому узлу дерева один и только

один раз.

Для каждого узла выполняются некоторые виды обработки (проверка, суммирование и т. п.), однако
способ обхода не зависит от конкретных действий и является общим для всех алгоритмов обработки узлов.

три способа посещения всех узлов, использующие обход в глубину:
Обход_слева_направо

(InOrder):
Обход_слева_направо левого поддерева;
обработать корень;
Обход_слева_направо правого поддерева.

Обход_снизу_вверх (PostOrder):
Обход_снизу_вверх левого поддерева;
Обход_снизу_вверх правого поддерева;
обработать корень.

узла N значение левого дочернего узла меньше, чем значение

в N, а значение правого дочернего узла больше значения в N.
Если в дереве могут содержаться одинаковые значения, то программист должен сам определить, влево или вправо помещать значение, равное значению в родительском узле, т. е. соответствующее строгое неравенство заменить на нестрогое.

№

его узла количества узлов в левом и в правом

его поддеревьях различаются не более чем на 1.
Разумеется, идеально сбалансированное дерево имеет минимальную высоту по сравнению со всеми другими деревьями с тем же числом узлов..
Чтобы построить такое дерево, нужно располагать максимально возможное число узлов на всех уровнях, кроме самого нижнего. Это сделать просто, если распределять узлы поровну слева и справа от каждого узла.

№