- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Информация и информационные технологии. (Лекция 1)
Содержание
- 2. Тема № 1.1 Информация и информационные технологии Лекция 1Информационные системы и технологии
- 3. «Технология ― совокупность производственных методов и процессов
- 4. Лекция 1Формы представления информации ― формы сообщения:сигналы
- 5. Лекция 1Информационные технологии можно понимать как совокупность
- 6. Лекция 1Информационные технологииПостоянные измененияСовременные информационные технологииНакопление информации
- 7. Лекция 1ИТ обработки данныхфункционально-ориентированные ИТ для реализации
- 8. Андрей Петрович Ершов: «О фазах продвижения к
- 9. Лекция 1Информационная сфераделовая информация (биржевая, финансовая,
- 10. Теория информации ― абстрактная теория слов
- 11. Лекция 1ИнформатикаИнформационные системы и технологии
- 12. Лекция 1Термин «информатика» согласно А.П.Ершову вводился в
- 13. Лекция 1Информатика завязана на создание информационной модели.
- 14. Лекция 1«Программирование ― это искусство, поскольку оно
- 15. Чл.-корр. АН СССРАлексей Андреевич Ляпунов (1911-1973)
- 16. Алексей Андреевич Ляпунов В начале 50-х
- 17. Андрей Петрович ЕРШОВ (1931-1988)Лекция 1Информационные системы и технологии
- 18. Андрей Петрович ЕРШОВ (1931-1988)1958 – первая в
- 19. Проблема IT-Индустрии: «индустриализация» труда программистаПротиворечие между традиционно
- 20. Проблема индустриализации программирования (взаимоотношения с «промышленностью»
- 21. «Программист должен обладать способностью первоклассного математика к
- 22. Лекция 1Выполнение программыИнформационные системы и технологии
- 23. Программа ― последовательность команд, которые заставляют выполнять
- 24. Компиляция (трансляция) /compilation (translation)/ ― перевод программы
- 25. Работа компилятораКомпилятоp предназначен для преобразования программы, написанной
- 26. Этапы компиляции:I. Анализ исходного кодаЛексический анализ ―
- 27. Этапы компиляции:II. Синтез выходного кодаОптимизация кода ―
- 28. Лекция 1Формальные языки и формальные грамматикиТема № 1.2Информационные системы и технологии
- 29. Основные определенияИнформационные системы и технологииЛекция 1Алфавит ―
- 30. Формальный язык — это множество конечных слов
- 31. Распознать — в результате процедуры специального вида
- 32. Порождающая грамматика• T — алфавит терминальных символов•
- 33. Вывод цепочки — это последовательность строк, состоящих
- 34. ВыводимостьИнформационные технологииЛекция 1
- 35. ПримерыИнформационные технологииЛекция 1так как существует вывод:Грамматики G1
- 36. Построить вывод цепочки для грамматики с правиламиT
- 37. Дерево вывода — это способ представления множества
- 38. Пример: The little boy runs quicklyГрамматический разбор
- 39. Терминальный алфавит:
- 40. Классификация грамматик по ХомскомуИнформационные технологииЛекция 1Рассматривается четыре
- 41. Классификация грамматик по ХомскомуИнформационные технологииЛекция 1Тип 2
- 42. Иерархия Хомского для грамматикИнформационные технологииЛекция 1Любая регулярная
- 43. Иерархия Хомского для классов языковИнформационные технологииЛекция 1
- 44. Распознающая грамматика позволяет по данному слову определить, входит оно в язык или нетРаспознающая грамматикаИнформационные технологииЛекция 1
- 45. Информационные системы и технологииТема № 1.3 Автоматы и деревья Лекция 1
- 46. Основные определенияПусть A = B = {0,
- 47. Примеры детерминированных функций:Лекция 1Информационные системы и технологии
- 48. ДеревьяНа ребрах записаны элементы образа при условии,
- 49. От деревьев к диаграммам переходовВведем нумерацию поддеревьев.Для
- 50. Функции перехода и выходаЛекция 1В каждой паре
- 51. Лекция 1Найдем функции перехода и выхода для
- 52. Построить вывод цепочки для грамматики с правилами:T
- 53. Построить вывод цепочки для грамматики с правилами:T
- 54. Построить вывод цепочки для грамматики с правилами:T
- 55. Построить вывод цепочки для грамматики с правилами:T
- 56. Скачать презентацию
- 57. Похожие презентации
















































Слайд 2
Тема № 1.1
Информация и информационные технологии
Лекция 1
Информационные системы
и технологии
Слайд 3 «Технология ― совокупность производственных методов и процессов отрасли
производства, а также научное описание способов производства...» (Ожегов С.И.
Толковый словарь русского языка / С.И. Ожегов, Н.Ю. Шведова. – М.: ООО «ИТИ Технологии», 2003.)Лекция 1
Информация существует в виде различных материальных форм, тогда как сама по себе является общим абстрактным содержанием в различных формах представления.
В различных областях науки существуют свои определения понятия «информация».
Информационные системы и технологии
Слайд 4
Лекция 1
Формы представления информации ― формы сообщения:
сигналы (физические
величины или свойства физической среды)
изображения (многомерные пространственные сигналы)
знаки (повторяющиеся
образцы сигналов)анализ и обработка сигналов
распознавание образов
информатика – сбор, хранение, поиск, обработка и выдача информации в знаковой форме
Информационные системы и технологии
Слайд 5
Лекция 1
Информационные технологии можно понимать как совокупность средств
и методов сбора, обработки и передачи данных для получения
информации нового качества о состоянии объекта, процесса или явления.Данные ― факты, идеи, сведения в знаковой форме, позволяющей производить их передачу, обработку и интерпретацию
Информационные системы и технологии
Слайд 6
Лекция 1
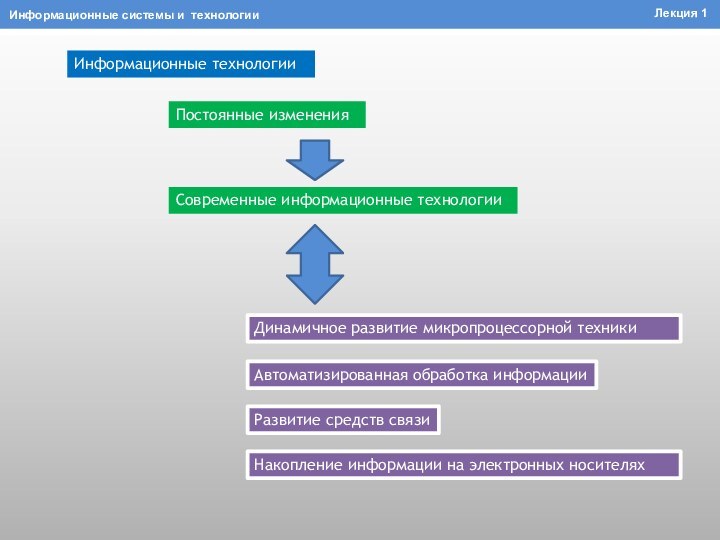
Информационные технологии
Постоянные изменения
Современные информационные технологии
Накопление информации на
электронных носителях
Развитие средств связи
Динамичное развитие микропроцессорной техники
Автоматизированная обработка информации
Информационные
системы и технологии
Слайд 7
Лекция 1
ИТ обработки данных
функционально-ориентированные ИТ для реализации определенных
задач
технологии обработки текстовой информации
Классификации информационных технологий:
ИТ управления
ИТ автоматизации офиса
ИТ
поддержки принятия решенийИТ экспертных систем
предметно-ориентированные ИТ для решения конкретны задач в определенной сфере
проблемно-ориентированные ИТ для решения типовых прикладных задач
технологии обработки числовой информации
технологии обработки графической информации
технологии обработки звуковой информации
технологии работы в глобальных сетях
социальные информационные технологии
Информационные системы и технологии
Слайд 8 Андрей Петрович Ершов: «О фазах продвижения к информационному
обществу следует судить по совокупным пропускным способностям каналов связи»
Лекция
1Этапы информатизации общества
Изобретение письменности
Изобретение книгопечатания (середина XVI века)
Прогресс средств связи (конец XIX века)
Появление микропроцессорной техники (70-ые гг. XX века)
Информационное общество
Информатизация общества влечет за собой отток людей из сферы прямого материального производства в информационную сферу
(вторая половина XX века)
Информационные системы и технологии
Слайд 9
Лекция 1
Информационная сфера
деловая информация
(биржевая, финансовая, статистическая, коммерческая
информация);
профессиональная информация
(научно-техническая информация, первоисточники и пр.);
потребительская информация
(новости, всевозможные расписания,
развлекательная информация);услуги образования
другое
информационный кризис
применение информационных технологий
Информационные системы и технологии
Слайд 10 Теория информации ― абстрактная теория слов со своими
специфическими задачами, связанными с их хранением в памяти компьютера,
обработкой и передачей по каналам связи.Лекция 1
Алгебраический подход:
Символ ― знак, который имеет специальный смысл.
Исходных знаков для представления информации не достаточно.
Получить из конечного множества знаков неограниченный запас сообщений можно путем составления последовательностей первичных знаков.
Формальная математическая модель ― формальные языки.
Информационные системы и технологии
Слайд 12
Лекция 1
Термин «информатика» согласно А.П.Ершову вводился в российскую
науку 3 раза:
[середина XX века] обозначение некоторой дисциплины, занимающейся
обработкой научно-технической информации. "информатика ― наука о научно-технической информации". [1976 г.] после издания перевода книги Ф.Л. Пауэра и Т. Гооза "Введение в информатику", термин начал соответствовать определению «Informatique » (фр.) и «Computer science »(англ.).
[Ершов] Информатика ― фундаментальная естественная наука, изучающая процессы передачи и обработки информации.
Информационные системы и технологии
Слайд 13
Лекция 1
Информатика завязана на создание информационной модели. То
есть сама информатика ― методология создания информационной модели и
методов использования таких моделей.Общие принципы принадлежат информатике, в то время как сами модели ― результат частных наук, дающих материал и исходные данные для создания моделей.
Понятие модели в технике связано с "имитационным моделированием", но не ограничено им. В информатике ― модели информационные.
Информационные системы и технологии
Слайд 14
Лекция 1
«Программирование ― это искусство, поскольку оно является
приложением накопленных знаний для практических целей, поскольку оно требует
умения и мастерства, и в особенности потому, что продукты программирования могут представлять эстетическую ценность»Дональд Кнут,
Тьюринговская лекция 1974 г.
Информационные системы и технологии
Слайд 15
Чл.-корр. АН СССР
Алексей Андреевич Ляпунов
(1911-1973)
Основатель советской
кибернетики и программирования
общие вопросы кибернетики
математические основы программирования
теория алгоритмов
математическая лингвистика
1954 г. МГУ Большой семинар по кибернетике
Лекция 1
Информационные системы и технологии
Слайд 16
Алексей Андреевич Ляпунов
В начале 50-х годов
создает основы программирования на ЭВМ: операторный метод ― язык
программированияАлгебраическая теория программирования
Автоматическое программирование:
«программирующие программы» ― трансляторы
Механико-математический факультет МГУ:
1953 – семинар по программированию
1954 – первый выпуск по специальности «программирование»
Лекция 1
Информационные системы и технологии
Слайд 18
Андрей Петрович ЕРШОВ (1931-1988)
1958 – первая в мировой
практике монография по трансляции:
Программирующая программа для быстродействующей электронной счетной
машины. – М.: Изд. АН СССР, 1958. - 116с.Programming programme for the BESM computer. –London a.o.: Pergamon Press, 1959. – 158p.
Первый оптимизирующий транслятор Альфа:
Многопроходная система трансляции. Оптимизирующие преобразования промежуточного представления программ. АЛЬФА-6 (1973), АИСТ, проект БЕТА: внутренний язык.
Язык СИГМА – символьная обработка, генерация программ
Лекция 1
Информационные системы и технологии
Слайд 19
Проблема IT-Индустрии:
«индустриализация»
труда программиста
Противоречие между традиционно высоким
уровнем фундаментального образования в Российской высшей школе и недостаточным
уровнем базового образования на программистских специальностях: подмена базового образования «тренингом»Лекция 1
Информационные системы и технологии
Слайд 20
Проблема индустриализации программирования
(взаимоотношения с «промышленностью» )
«Конвейерный метод
в программировании может либо убить интеллектуальную компоненту в труде
программиста, либо вызвать неврозы…»А.П.Ершов, 1972 г.
«Программирование – это слишком сложное интеллектуальное занятие, чтобы можно было надеяться навязать ему узы иерархической системы, которая душит всякую инициативу»
Б.Мейер, К.Бодуэн, 1982 (1978) г.
Лекция 1
Информационные системы и технологии
Слайд 21
«Программист должен обладать способностью первоклассного математика к абстракции
и логическому мышлению в сочетании с эдисоновским талантом сооружать
все, что угодно, из нуля и единицы»А.П.Ершов
Лекция 1
Информационные системы и технологии
Слайд 23 Программа ― последовательность команд, которые заставляют выполнять указанные
в них действия с содержимым указанных ячеек памяти.
Программа на
алгоритмическом языке также состоит из последовательности команд, но записанных без явного описания ячеек памяти.Эквивалентные программы ― программы, решающие одну и ту же задачу и дающие на выходе одинаковые результаты при одинаковых исходных данных.
Лекция 1
Информационные системы и технологии
Слайд 24 Компиляция (трансляция) /compilation (translation)/ ― перевод программы с
одного языка на другой язык:
Преобразование текста с одного языка
в семантически эквивалентный текст на другом языке.Лекция 1
Компилятор ― языковой процессор (программа), который воспринимает программу на некотором входном языке в качестве входных данных, а на выходе выдает эквивалентную программу на другом языке.
Задача ― получить эквивалентную программу
Информационные системы и технологии
Слайд 25
Работа компилятора
Компилятоp предназначен для преобразования программы, написанной на
алгоритмическом языке, в эквивалентную программу на машинном языке
Анализирующая часть
компилятора разбивает исходную программу на составляющие ее элементы (конструкции языка) и создает промежуточное представление исходной программы (выделяет более «крупные» единицы для последующего разбора)Синтезирующая часть компилятора, в соответствии с некоторой грамматикой, разбивает промежуточное представление программы и создает программу в машинных кодах
Лекция 1
Информационные системы и технологии
Слайд 26
Этапы компиляции:
I. Анализ исходного кода
Лексический анализ ― символы
группируются в лексические единицы (идентификаторы, служебные слова, операторы, знаки
препинания)Синтаксический анализ ― составление из лексических единиц иерархических структур, результат ― деревья синтаксического анализа
Семантический анализ ― генерация промежуточного кода ― программа на языке абстрактного синтаксиса
Лекция 1
Информационные системы и технологии
Слайд 27
Этапы компиляции:
II. Синтез выходного кода
Оптимизация кода ― преобразование
последовательности команд с целью уменьшения их количества, выделение инвариантов,
исключение повторяющихся фрагментов и т.д.Генератор кода ― формирование текста программы на новом языке.
Лекция 1
Информационные системы и технологии
Слайд 28
Лекция 1
Формальные языки
и
формальные грамматики
Тема № 1.2
Информационные
системы и технологии
Слайд 29
Основные определения
Информационные системы и технологии
Лекция 1
Алфавит ― конечное
непустое множество знаков ∑
Слово (или цепочка) над алфавитом ―
конечная упорядоченная последовательность элементов множества ∑Пустая цепочка ε в алфавит не входит!
Для цепочек α и β определена операция конкатенции α•β = αβ
Для любой цепочки α выполняется α•ε = ε•α = α
Конкатенция – ассоциативная операция α•(β•γ)=(α•β)•γ=α•β•γ
Длина цепочки ω обозначается |ω|, полагаем |ε| = 0
Степень цепочки αk = αα … αα и обращение цепочки αR
Степень алфавита множество всех слов соответствующей длины
Через ∑* обозначается множество всех возможных слов над алфавитом ∑ и пустая ε
Множество всех возможных непустых слов над алфавитом ∑ обозначается как ∑+
Получаем ∑* = ∑+ {ε}
k
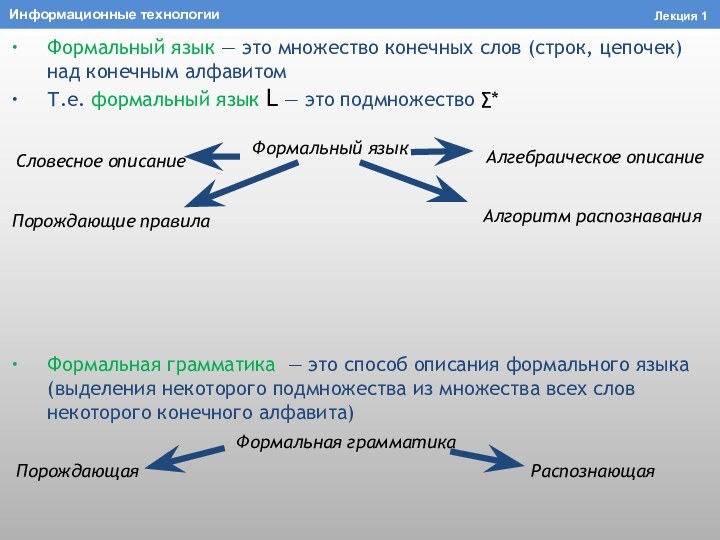
Слайд 30 Формальный язык — это множество конечных слов (строк,
цепочек) над конечным алфавитом
Т.е. формальный язык L — это
подмножество ∑*Формальная грамматика — это способ описания формального языка (выделения некоторого подмножества из множества всех слов некоторого конечного алфавита)
Информационные технологии
Лекция 1
Формальный язык
Словесное описание
Алгебраическое описание
Порождающие правила
Алгоритм распознавания
Формальная грамматика
Порождающая
Распознающая
Слайд 31
Распознать — в результате процедуры специального вида по
заданной цепочке определить, принадлежит ли она языку.
Примеры:
Машина
Тьюринга (МТ)Линейно ограниченный автомат (МТ с конечной лентой, ограниченной длиной входного слова) – не детерминированный
Автомат с внешней памятью (имеется дополнительная бесконечная память)
Конечный автомат
Порождать — на основе набора инструкций из начального множества символов построить все цепочки языка
Информационные технологии
Лекция 1
Слайд 32
Порождающая грамматика
• T — алфавит терминальных символов
• N
— алфавит нетерминальных символов
• P — конечное множество правил
вывода• S — начальный символ грамматики (S ∈ N)
G = (T, N, P, S)
Порождающая грамматика задает правила, с помощью которых можно построить любое слово языка
Информационные технологии
Лекция 1
Терминал (терминальный символ) — это объект, непосредственно присутствующий в словах языка, соответствующего грамматике и имеющий конкретное, неизменяемое значение (0, 1, 2, 3, 4, 5, 6, a, b, c и т.д.)
Нетерминал (нетерминальный символ) — это объект, обозначающий какую-либо сущность языка (ФОРМУЛА, ВЫРАЖЕНИЕ, КОМАНДА и т.д.) и не имеющий конкретного символьного значения
Слайд 33 Вывод цепочки — это последовательность строк, состоящих из
терминальных и нетерминальных символов, где первая строка состоит из
одного начального нетерминального символа, а каждая последующая строка получена из предыдущей путем замены некоторой подстроки по одному (любому) из правил.Конечная строка полностью состоит из терминальных символов и является словом языка
Вывод цепочки
Понятие выводимости:
Если αYβ последовательный набор символов языка G, а
Y→x («х непосредственно выводится из Y») правило этого языка, то набор символов αxβ непосредственно выводится из набора символов αYβ в языке G
αYβ → αxβ
Информационные технологии
Лекция 1
Слайд 35
Примеры
Информационные технологии
Лекция 1
так как существует вывод:
Грамматики G1 и
G2 называются эквивалентными, если L(G1) = L(G2)
Грамматики G1
и G2 называются почти эквивалентными, если языки L(G1) и L(G2) отличаются не более чем на ε
Слайд 36
Построить вывод цепочки для грамматики с правилами
T =
{a, b, +}
N = {S, T}
G = (a+b+a)
P: S → T | T+S
Т → a | b
Вывод цепочки
1 способ
S→T+S→a+S→a+T+S→a+b+S→a+b+T→a+b+a
2 способ
S→T+S→T+T+S→T+T+T→T+T+a→T+b+a→a+b+a
3 способ
S→T+S→T+T+S→T+T+T→a+T+T→a+b+T→a+b+a
Информационные технологии
Лекция 1
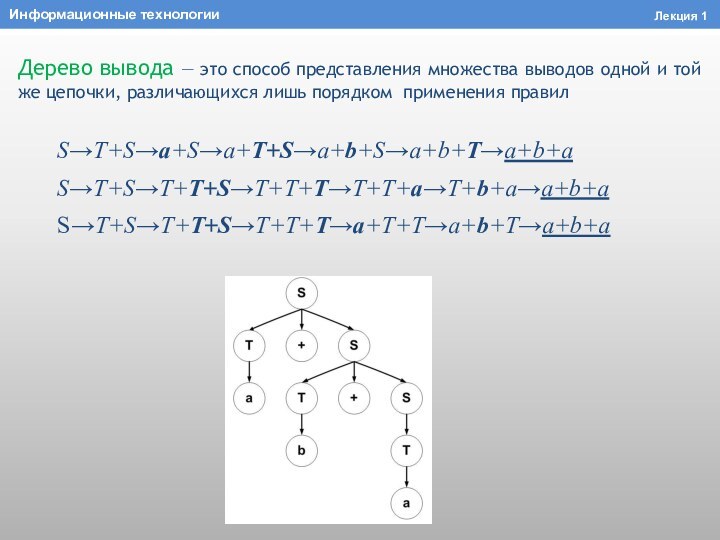
Слайд 37 Дерево вывода — это способ представления множества выводов
одной и той же цепочки, различающихся лишь порядком применения
правилS→T+S→a+S→a+T+S→a+b+S→a+b+T→a+b+a
S→T+S→T+T+S→T+T+T→T+T+a→T+b+a→a+b+a
S→T+S→T+T+S→T+T+T→a+T+T→a+b+T→a+b+a
Информационные технологии
Лекция 1
Слайд 38
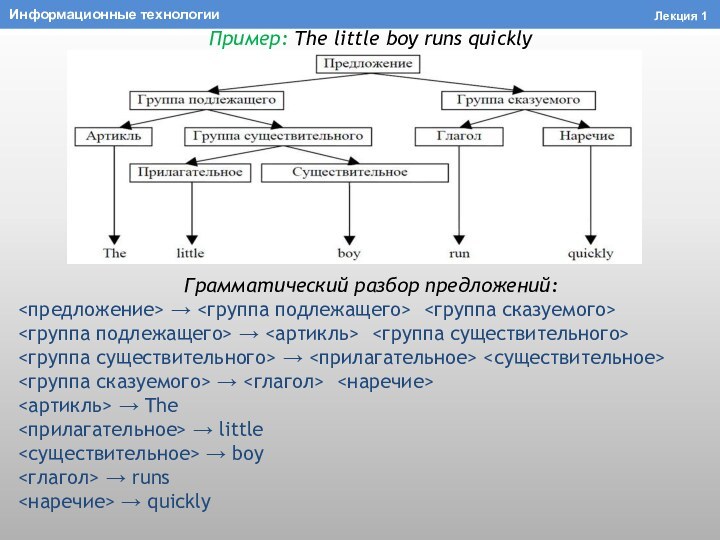
Пример: The little boy runs quickly
Грамматический разбор предложений:
→
→
существительного><группа существительного> → <прилагательное> <существительное>
<группа сказуемого> → <глагол> <наречие>
<артикль> → The
<прилагательное> → little
<существительное> → boy
<глагол> → runs
<наречие> → quickly
Информационные технологии
Лекция 1
Слайд 39 Терминальный алфавит:
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +, -, *, /, (, )}
Нетерминальный алфавит: {ФОРМУЛА, ЗНАК, ЧИСЛО, ЦИФРА}
Правила:
1. ФОРМУЛА → ФОРМУЛА ЗНАК ФОРМУЛА (формула есть две формулы, соединенные знаком)
2. ФОРМУЛА → ЧИСЛО (формула есть число)
3. ФОРМУЛА → (ФОРМУЛА) (формула есть формула в скобках)
4. ЗНАК → + | - | * | / (знак есть плюс или минус или умножить или разделить)
5. ЧИСЛО → ЦИФРА (число есть цифра)
6. ЧИСЛО → ЧИСЛО ЦИФРА (число есть число и цифра)
7. ЦИФРА → 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 (цифра есть 0 или 1 или ... 9 )
Начальный нетерминал: ФОРМУЛА
Результат: (12 + 5)
ФОРМУЛА → 3 (ФОРМУЛА)
(ФОРМУЛА) → 1 (ФОРМУЛА ЗНАК ФОРМУЛА)
(ФОРМУЛА ЗНАК ФОРМУЛА) → 4 (ФОРМУЛА + ФОРМУЛА)
(ФОРМУЛА + ФОРМУЛА) → 2 (ФОРМУЛА + ЧИСЛО)
(ФОРМУЛА + ЧИСЛО) → 5 (ФОРМУЛА + ЦИФРА)
(ФОРМУЛА + ЦИФРА) → 7 (ФОРМУЛА + 5)
(ФОРМУЛА + 5) → 2 (ЧИСЛО + 5)
(ЧИСЛО + 5) → 6 (ЧИСЛО ЦИФРА + 5)
(ЧИСЛО ЦИФРА + 5) → 5 (ЦИФРА ЦИФРА + 5)
(ЦИФРА ЦИФРА + 5) → 7 (1 ЦИФРА + 5)
(1 ЦИФРА + 5) → 7 (12 + 5)
Информационные технологии
Лекция 1
Слайд 40
Классификация грамматик по Хомскому
Информационные технологии
Лекция 1
Рассматривается четыре типа
грамматик, называемых:
тип 0
тип 1
тип 2
тип 3
Тип 0 ― неограниченная
грамматикалюбая порождающая грамматика является грамматикой типа 0
Тип 1 ― контекстно-зависимая грамматика (КЗ)
каждое правило имеет вид: γ1Aγ2 → γ1βγ2, где γi из ∑* , β из ∑+ , A из N
Тип 1 ― неукорачивающая грамматика
если правая часть каждого правила вывода не короче левой части
Если L ― формальный язык, то следующие утверждения эквивалентны:
Существует контекстно-зависимая грамматика G1: L= L(G1)
Существует неукорачивающая грамматика G2: L= L(G2)
Слайд 41
Классификация грамматик по Хомскому
Информационные технологии
Лекция 1
Тип 2 ―
контекстно-свободная грамматика (КС)
каждое правило имеет вид: A → β,
где β из ∑* , A из NДля любой контекстно-свободной грамматики G существует неукорачивающая грамматика
G`: L (G ) = L(G`)
Тип 3 ― регулярная (праволинейная, леволинейная) грамматика
праволинейная: каждое правило из P имеет вид A → wB или A → w, где
A и B из N, w из T*
леволинейная: каждое правило из P имеет вид A → Bw или A → w, где
A и B из N, w из T*
Если L ― формальный язык, то следующие утверждения эквивалентны:
Существует праволинейная грамматика G1: L= L(G1)
Существует леволинейная грамматика G2: L= L(G2)
т.е. праволинейные и леволинейные грамматики определяют один и тот же класс языков,
такие языки называются регулярными
Автоматная ― праволинейная грамматика, где каждое правило с непустой правой частью имеет вид
A → a или A → aB, где A, B из N, a из T.
Слайд 42
Иерархия Хомского для грамматик
Информационные технологии
Лекция 1
Любая регулярная грамматика
является КС-грамматикой
Любая неукорачивающая КС-грамматика является КЗ-грамматикой
Любая неукорачивающая грамматика является
грамматикой типа 0
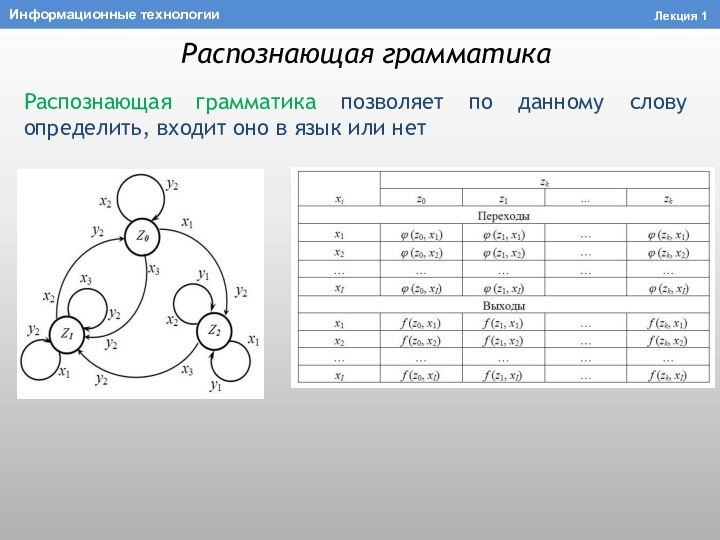
Слайд 44 Распознающая грамматика позволяет по данному слову определить, входит
оно в язык или нет
Распознающая грамматика
Информационные технологии
Лекция 1
Слайд 46
Основные определения
Пусть A = B = {0, 1}
Рассмотрим
f такую, что нулевая последовательность переходит в себя, а
остальные переводятся в последовательность из одних единиц.Тогда если w = (0,0, … ) для определения f(w) недостаточно знать конечное число элементов w.
Рассматриваем два алфавита – конечные множества A и B
И последовательности букв из A и B:
(a(1), a(2), …, a(t), …) и (b(1), b(2), …, b(t), …)
И отображения f: A* B*
Лекция 1
Функция f: (a(1), a(2), …, a(t), …) (b(1), b(2), …, b(t), …) называется детерминированной, если b(t) однозначно определяется первыми t членами.
a(1), a(2), …, a(t).
Информационные системы и технологии
Слайд 48
Деревья
На ребрах записаны элементы образа при условии, что
0 элементу прообраза соответствует движение влево,
1 элементу прообраза соответствует
движение вправо.Детерминированные функции можно задавать на бесконечных деревьях:
Лекция 1
Конечно детерминированные функции или автоматы – детерминированные функции
в деревьях которых содержится лишь конечное число различных (не изоморфных между
собой) поддеревьев. Изоморфизм здесь подразумевается как биекция, сохраняющая
записанные на ребрах буквы.
Информационные системы и технологии
Слайд 49
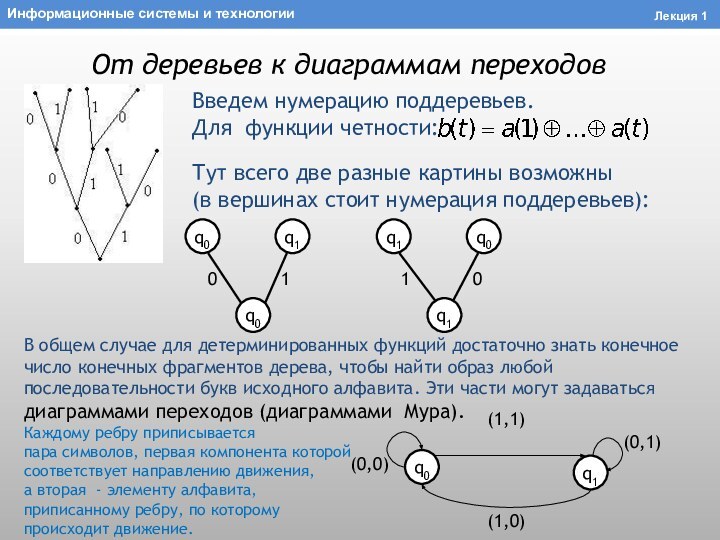
От деревьев к диаграммам переходов
Введем нумерацию поддеревьев.
Для функции
четности:
Тут всего две разные картины возможны
(в вершинах стоит
нумерация поддеревьев):Лекция 1
В общем случае для детерминированных функций достаточно знать конечное число конечных фрагментов дерева, чтобы найти образ любой последовательности букв исходного алфавита. Эти части могут задаваться диаграммами переходов (диаграммами Мура).
Каждому ребру приписывается
пара символов, первая компонента которой
соответствует направлению движения,
а вторая - элементу алфавита,
приписанному ребру, по которому
происходит движение.
q0
1
0
0
1
q1
q0
q0
q1
q1
(0,1)
(0,0)
(1,1)
(1,0)
q0
q1
Информационные системы и технологии
Слайд 50
Функции перехода и выхода
Лекция 1
В каждой паре первая
компонента – это какая-нибудь буква из A, а вторая
– буква из B, которая получается, если в состоянии (оно же номер поддерева), записанном в вершине, из которой выходит ребро, поддать эту букву из A:Автоматные функции можно задавать двумя функциями:
функцией перехода G(a(t), q(t)) = q(t+1)
функцией выхода F(a(t), q(t)) = b(t)
q(t) – состояние в момент t
a(t) – очередная буква, подданная на вход,
b(t) – очередная буква на выходе.
Удобно по умолчанию считать q(0) = 0, когда это имеет смысл.
Для функции четности:
q
G(a, q)
(a, F(a, q))
Информационные системы и технологии
Слайд 51
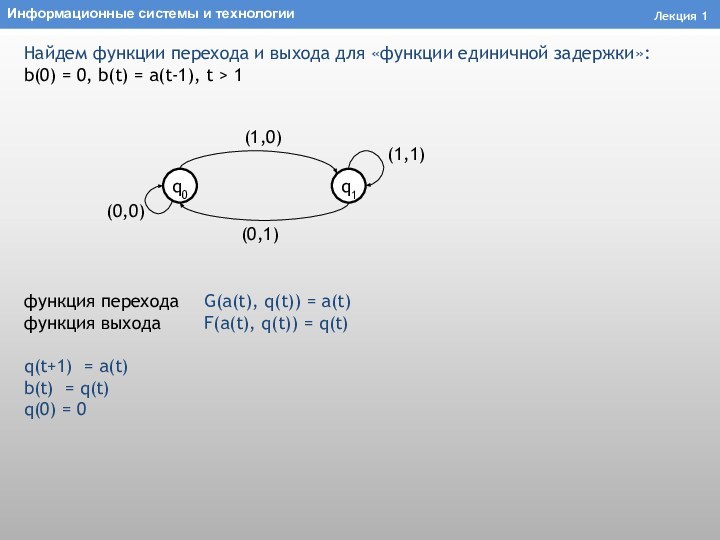
Лекция 1
Найдем функции перехода и выхода для «функции
единичной задержки»:
b(0) = 0, b(t) = a(t-1), t >
1функция перехода G(a(t), q(t)) = a(t)
функция выхода F(a(t), q(t)) = q(t)
q(t+1) = a(t)
b(t) = q(t)
q(0) = 0
(1,1)
(0,0)
(1,0)
(0,1)
q0
q1
Информационные системы и технологии
Слайд 52
Построить вывод цепочки для грамматики с правилами:
T =
{a, b, c} N = {B, C,
S} G = (aaabbbccc)P: S → aSBC | abC
CB → BC
bB → bb
bC → bc
cC → cc
Задача №1
Лекция 1
Информационные системы и технологии
Слайд 53
Построить вывод цепочки для грамматики с правилами:
T =
{a, b, c} N = {A,B,S}
G = (aabcaab)P: S → aAS | bBS | c
Aa → aA
Ab → bA
Ac → ca
Ba → aB
Bb → bB
Bc → cb
Задача №2
Лекция 1
Информационные системы и технологии
Слайд 54
Построить вывод цепочки для грамматики с правилами:
T =
{a, b, c} N = {A, B,
S} G = (aabbab)P: S→ aB | bА | ε
B → bS | аВВ
А → аS | bAA
Задача №3
Лекция 1
Информационные системы и технологии
Слайд 55
Построить вывод цепочки для грамматики с правилами:
T =
{a, b} N = {T, F, S}
G = (a-b*a+b)P: S → T | T+S | T-S
T → F | F*T
F → a | b
Задача №4
Лекция 1
Информационные системы и технологии