Презентация на тему История систем счисления

к
 напряжению ума. 

Гаспа́р Монж, граф де Пелю́з
(10.5.1746-28.7.1818) —

французский математик,
геометр,
государственный деятель,
морской министр.

Майя
 Старо-Китайская нумерация
 Славянская кириллическая нумерация
 Славянская глаголическая нумерация
 Латинская нумерация
 Современная арабская нумерация

и др.

которой числа записываются по определенным правилам с помощью символов

некоторого алфавита, которые называют цифрами.

цифры не зависит от ее положения в числе.
Непозиционные
системы

счисления

цифры зависит от ее положения в числе.
Позиционные
системы счисления

дюймов, 1 шиллинг = 12 пенсов)
двадцатеричная (1 франк =

20 су)
шестидесятеричная (1 минута = 60 секунд, 1 час = 60 минут)

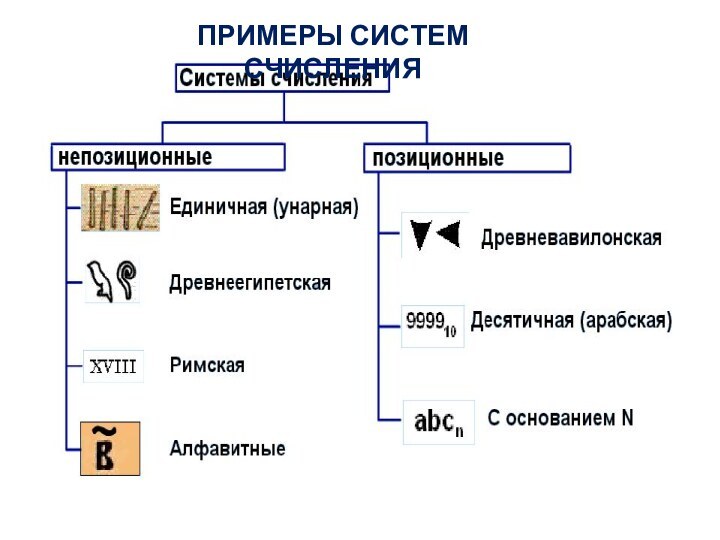
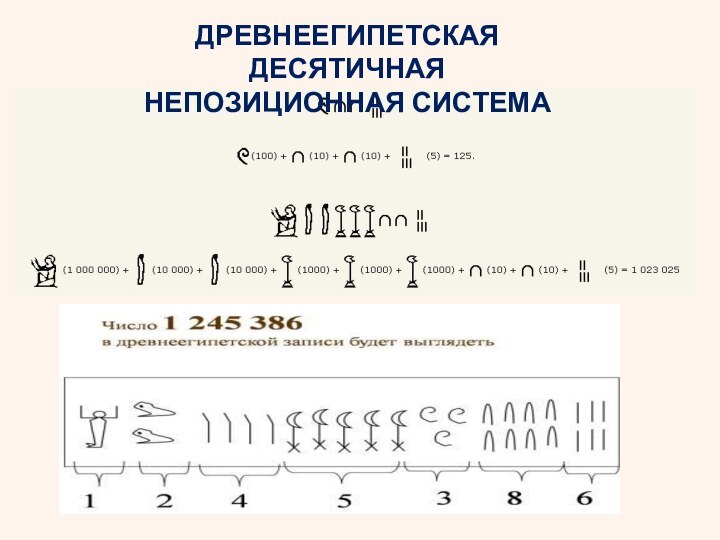
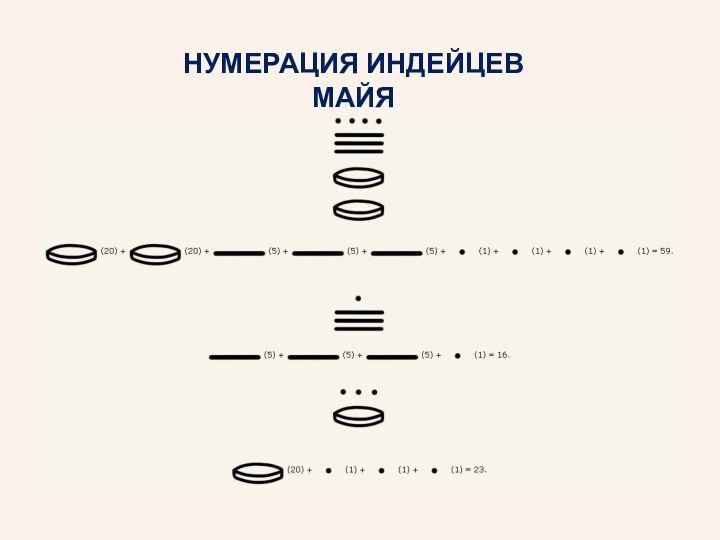
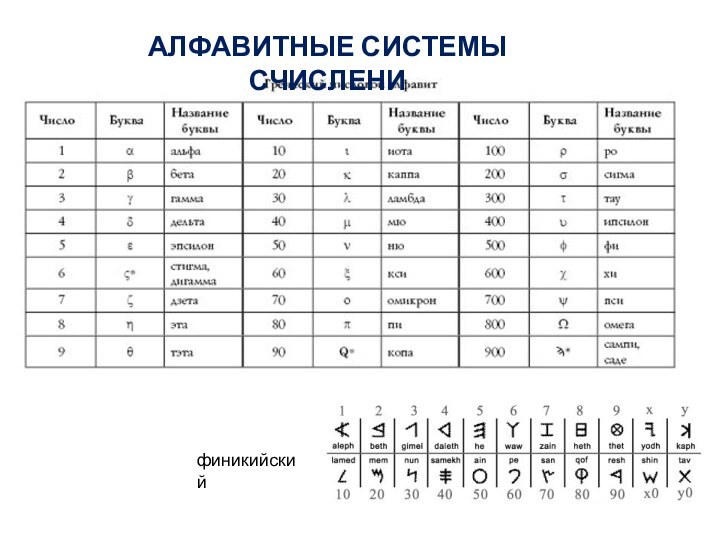
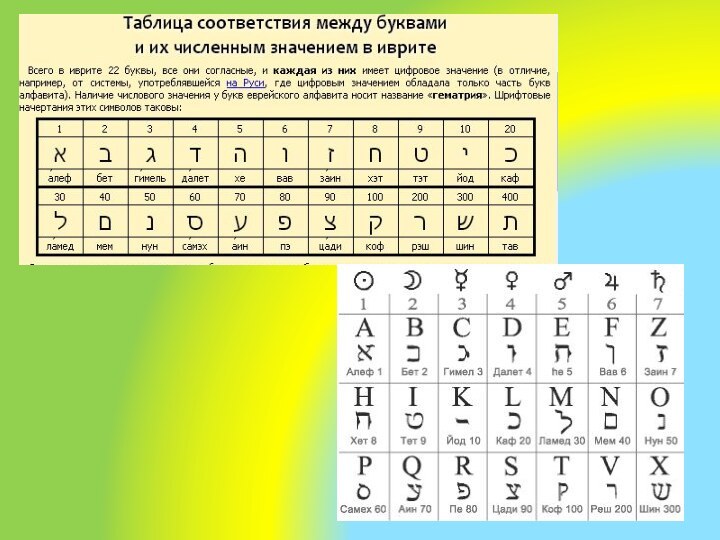
Примеры систем счисления

времена, как только люди начали считать. Количество предметов, например

овец, изображалось нанесением чёрточек или засечек на какой - либо твёрдой поверхности: камне, глине, дереве (до изобретения бумаги было ещё очень и очень далеко). Каждой овце в такой записи соответствовала одна чёрточка. Археологами найдены такие "записи" при раскопках культурных слоёв, относящихся к периоду палеолита (10 - 11 тысяч лет до н.э.).
В этой системе счисления для записи чисел используется только одна цифра. Ее можно изобразить в виде палочки , кружочка , или любой другой фигуры. Числа будут записываться примерно так:
1 
2  
3   
4    
5      и т. д.


Такая система счисления использовалась, и до сих пор используется в основном народами, не имеющими письменности.
Учёные назвали этот способ записи чисел единичной ("палочной") системой счисления. В ней для записи чисел применялся только один вид знаков - "палочка". Каждое число в такой системе счисления обозначалось с помощью строки, составленной из палочек, количество которых и равнялось обозначаемому числу.
Неудобства такой системы записи чисел и ограниченность её применения очевидны: чем большее число надо записать, тем длиннее строка из палочек. Да и при записи большого числа легко ошибиться, нанеся лишнее количество палочек или, наоборот, не дописав их.

Единичная непозиционная система счисления

Унарная – одна цифра обозначает единицу (1 день, 1 камень, 1 баран, …)

5 000 лет тому назад. Это одна из древнейших систем

записи чисел, известная человеку. В древнеегипетской системе счисления, которая возникла во второй половине третьего тысячелетия до н.э., использовались специальные цифры для обозначения чисел 1, 10, 102, 103, 104, 105, 106, 107. Числа в египетской системе счисления записывались как комбинации этих цифр, в которых каждая из них повторялась не более девяти раз.

придумана еще в древнем Вавилоне, причем вавилонская нумерация была

шестидесятеричной, то есть в ней использовалось шестьдесят цифр.
Числа составлялись из знаков двух видов:
 Единицы –прямой клин
 Десятки – лежачий клин
  Сотни

на ее развитие не повлеяла ни одна из цивилизаций Старого Света.

Однако в ней использованы все те же принципы. Сначала эта нумерация обслуживала пятиричную систему счисления, а потом ее приспособили для двадцатиричной.

(раскрытая ладонь, 5 пальцев), X – 10 (две

ладони), L – 50, C – 100 (Centum), D – 500 (Demimille), M – 1000 (Mille)

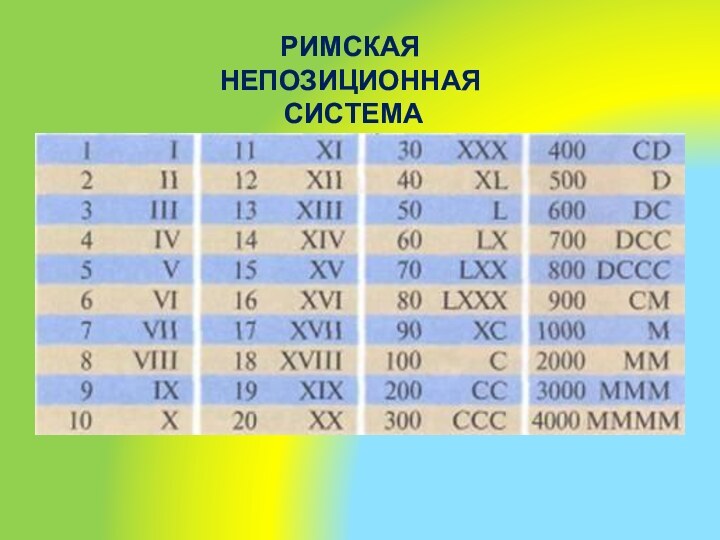
Римская непозиционная
система

+ 50 + 3*10 + 2 =

1782

+ 50 + 3*10 + 2 =
1782
Это год

открытия памятника.

На гранитном постаменте памятника Петру I
в Санкт- Петербурге есть римское число: