Презентация на тему Лекция 4-2. Основные понятия теории кодирования

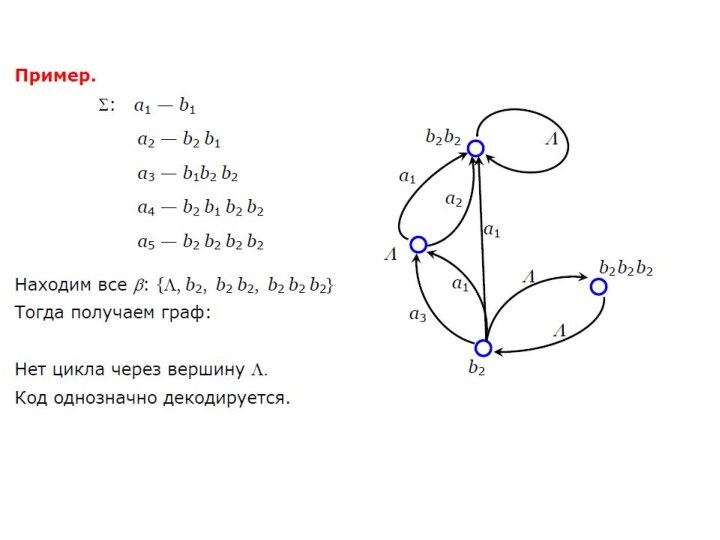
алфавитное
кодирование является взаимно-однозначным.

Таким образом, свойство префикса является достаточным условием

взаимной
однозначности.

кодирование. Пусть W — максимальное число кодовых слов, которые

«помещаются» подряд внутри кодового слова. Пусть li — длина слова Bi и

Тогда если кодирование φ не взаимно однозначно, то существуют два различных слова

существует некоторое слово , которое допускает две

расшифровки. Если слово не является неприводимым, то выбрасывая из куски несколько раз, получим неприводимое слово ; иначе, положим . Очевидно, это всегда можно сделать. Рассмотрим любые две декодировки слова . Разрежем слово в концевых точках кодовых слов каждого из разбиений.
Слова нового разбиения разделим на два класса: к I классу отнесём слова, являющиеся элементарными кодами, а ко II классу — все остальные слова (то есть слова, являющиеся началами кодовых слов одного разбиения и концами слов второго разбиения).

все слова β1, β2, …, βm II класса различны.
Доказательство.

Пусть β' = β''. Тогда, очевидно, слово не будет неприводимым, поскольку при выкидывании отрезка между β' и β'', вместе с любым из этих слов, получим снова две различные расшифровки этого слова (проверьте). Лемма доказана.

Таким образом, все β1, β2, …, βm разные. Тогда число слов второго класса не превосходит числа непустых начал элементарных кодов, то есть не превосходит

чем на L – r + 1 кусков. Рассмотрим

пары соседних кусков. Тогда согласно одному разбиению в одной половинке уложится не более одного кодового слова, а в другой — не более W (согласно второму разбиению ситуация симметрична). Всего пар кусков не больше, чем

а в каждом из них укладывается слов не более чем W + 1. Отсюда число кодовых слов в любом разбиении не превосходит

а поскольку число целое, то не превосходит и целой части

Теорема доказана.