при помощи т.н. базовых логических элементов, которые также еще
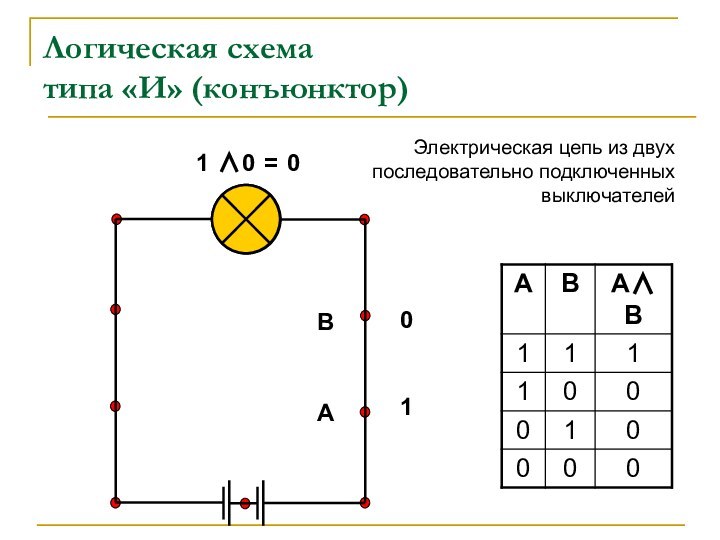
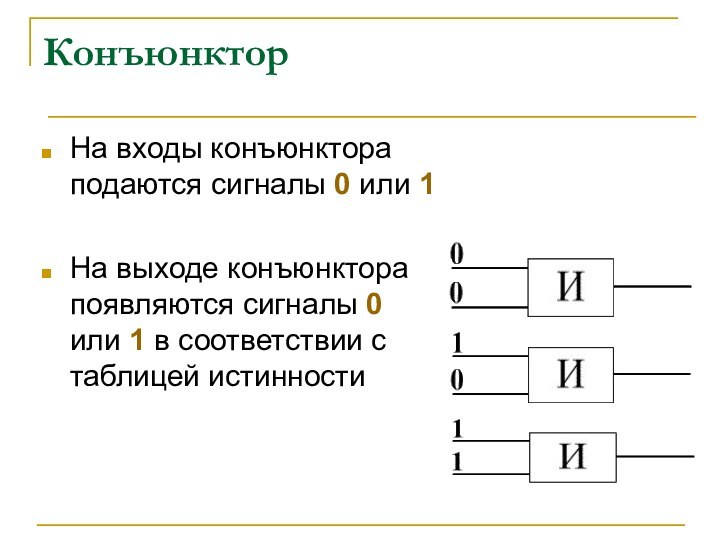
называют вентилями.Вентиль «И» – конъюнктор. Реализует конъюнкцию.
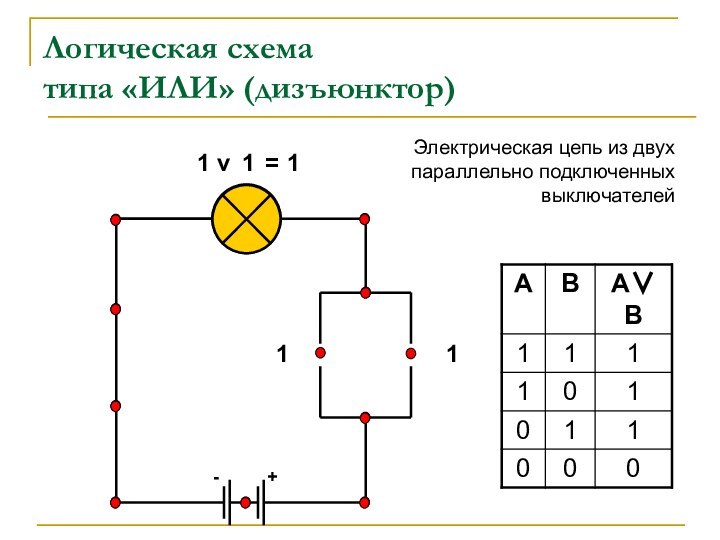
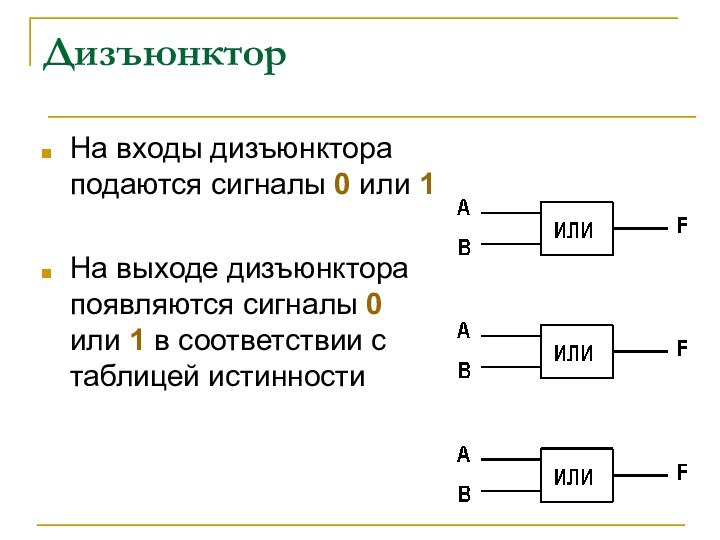
Вентиль «ИЛИ» – дизъюнктор. Реализует дизъюнкцию.
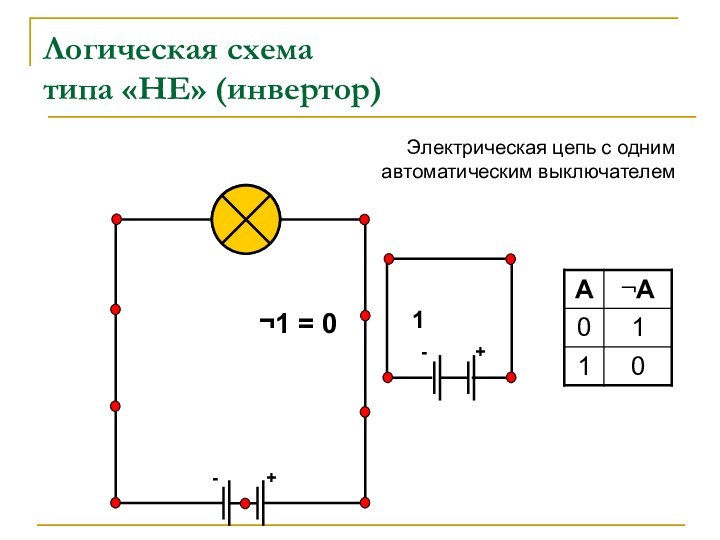
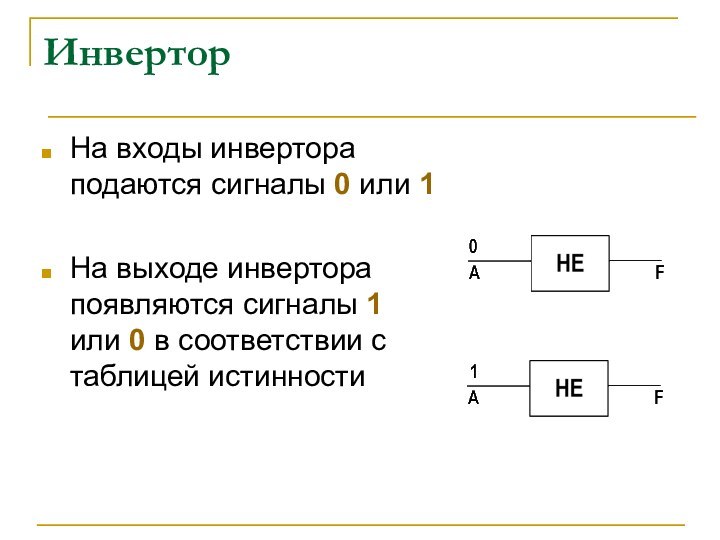
Вентиль «НЕ» – инвертор. Реализует инверсию
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Логические основы компьютера Базовые логические элементы
Содержание
- 2. Базовые логические элементыКомпьютер выполняет арифметические и логические
- 3. Составные элементыЛюбая логическая операция может быть представлена
- 4. Сигналы-аргументы и сигналы-функции Вентили оперируют с
- 5. Логическая схема типа «И» (конъюнктор)1∧0=010AВЭлектрическая цепь из двух последовательно подключенных выключателей
- 6. +-Логическая схема типа «ИЛИ» (дизъюнктор)111v1=1Электрическая цепь из двух параллельно подключенных выключателей
- 7. +-Логическая схема типа «НЕ» (инвертор)+-¬1 = 01Электрическая цепь с одним автоматическим выключателем
- 8. КонъюнкторНа входы конъюнктора подаются сигналы 0 или
- 9. ДизъюнкторНа входы дизъюнктора подаются сигналы 0 или
- 10. ИнвеpторНа входы инвертора подаются сигналы 0 или
- 11. Сумматор двоичных чиселЛюбое математическое сколь угодно сложное
- 12. Полусумматор. Арифметическое сложение двоичных чисел В каждом разряде
- 13. Обозначим слагаемые через А и В, перенос
- 14. Получаем формулу для вычисления SЕсли сравнить А∨В
- 15. Получаем формулу для вычисления SS = (А
- 16. Логическая схема двоичного полусумматора Полусумматор называется так,
- 17. Полный одноразрядный сумматор Должен иметь три входа (А, В и Р0) и два выхода (S и P)0001011101101001
- 18. Формула полного одноразрядного сумматораР принимает значение
- 19. Формула полного одноразрядного сумматора Правильное значение суммы
- 20. Многоразрядный сумматор Построен на основе полных одноразрядных сумматоров
- 21. ТриггерВажнейшая структурная единица оперативной памяти и регистров
- 22. Логическая схема триггераИЛИИЛИНЕНЕSRQ
- 23. Скачать презентацию
- 24. Похожие презентации
Базовые логические элементыКомпьютер выполняет арифметические и логические операции при помощи т.н. базовых логических элементов, которые также еще называют вентилями.Вентиль «И» – конъюнктор. Реализует конъюнкцию.Вентиль «ИЛИ» – дизъюнктор. Реализует дизъюнкцию.Вентиль «НЕ» – инвертор. Реализует
Слайд 2
Базовые логические элементы
Компьютер выполняет арифметические и логические операции
Вентиль «И» – конъюнктор. Реализует конъюнкцию.
Вентиль «ИЛИ» – дизъюнктор. Реализует дизъюнкцию.
Вентиль «НЕ» – инвертор. Реализует инверсию
Слайд 3
Составные элементы
Любая логическая операция может быть представлена через
конъюнкцию, дизъюнкцию и инверсию
Любой сколь угодно сложный элемент компьютера
может быть сконструирован из элементарных вентилей
Слайд 4
Сигналы-аргументы и
сигналы-функции
Вентили оперируют с электрическими импульсами:
Импульс имеется –
логический смысл сигнала «1»
Импульса нет –
логический смысл сигнала «0»На входы вентиля подаются импульсы – значения аргументов, на выходе вентиля появляется сигнал – значение функции
Слайд 5
Логическая схема
типа «И» (конъюнктор)
1
∧
0
=
0
1
0
A
В
Электрическая цепь из двух
последовательно подключенных
выключателей
Слайд 6
+
-
Логическая схема
типа «ИЛИ» (дизъюнктор)
1
1
1
v
1
=
1
Электрическая цепь из двух
параллельно подключенных
выключателей
Слайд 7
+
-
Логическая схема
типа «НЕ» (инвертор)
+
-
¬1 = 0
1
Электрическая цепь
с одним
автоматическим выключателем
Слайд 8
Конъюнктор
На входы конъюнктора подаются сигналы 0 или 1
На
выходе конъюнктора появляются сигналы 0 или 1 в соответствии
с таблицей истинности
Слайд 9
Дизъюнктор
На входы дизъюнктора подаются сигналы 0 или 1
На
выходе дизъюнктора появляются сигналы 0 или 1 в соответствии
с таблицей истинности
Слайд 10
Инвеpтор
На входы инвертора подаются сигналы 0 или 1
На
выходе инвертора появляются сигналы 1 или 0 в соответствии
с таблицей истинности
Слайд 11
Сумматор двоичных чисел
Любое математическое сколь угодно сложное выражение
может быть представлено в виде последовательности элементарных математических операций
Все
математические действия в компьютере сводятся к сложению двоичных чиселОснову микропроцессора составляют сумматоры двоичных чисел
Слайд 12
Полусумматор. Арифметическое сложение двоичных чисел
В каждом разряде образуется
сумма цифр в соответствующих разрядах слагаемых, при этом возможен
перенос единицы в старший разрядБез переноса
0000 0001
0000 0010
0
0
0
0
0
0
1
1
С переносом
0000 0011
0000 0010
0
0
0
0
0
1
0
1
+
+
Слайд 13 Обозначим слагаемые через А и В, перенос –
через Р, а сумму – через S
Таблица сложения
одноразрядных двоичных чисел: 0
0
0
1
0
1
1
0
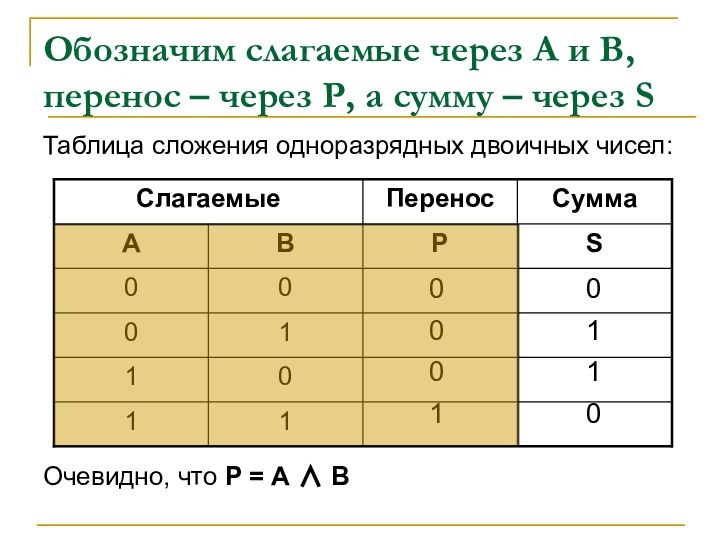
Очевидно, что Р = А ∧ В
Слайд 14
Получаем формулу для вычисления S
Если сравнить А∨В c
S:
то очевидно, что они практически идентичны.
Чтобы равенство оказалось полным
нужно выражение А∨В умножить на ¬Р
Слайд 15
Получаем формулу для вычисления S
S = (А ∨
В) ∧ ¬P ⇒ (А ∨ В) ∧ ¬(A
∧ B)0
1
1
1
0
0
0
1
1
1
1
0
0
1
1
0
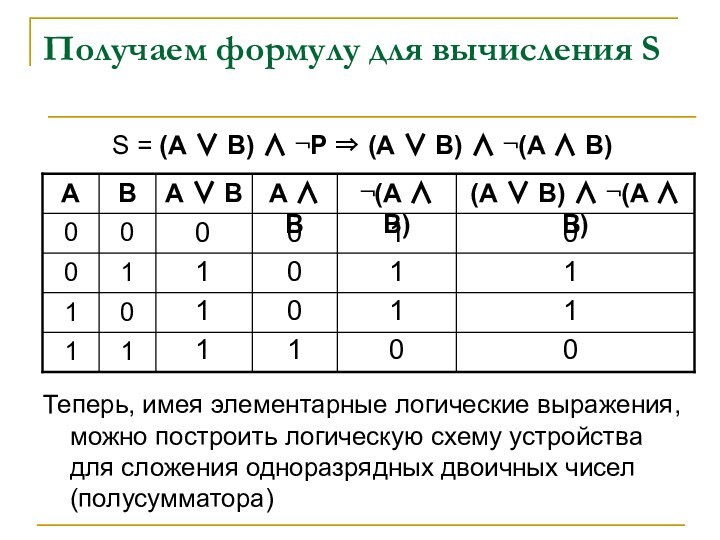
Теперь, имея элементарные логические выражения, можно построить логическую схему устройства для сложения одноразрядных двоичных чисел (полусумматора)
Слайд 16
Логическая схема
двоичного полусумматора
Полусумматор называется так, потому, что
здесь не учитывается перенос единицы из младшего разряда
И
НЕ
И
ИЛИ
А
B
А ∧
ВА ∨ В
¬(А ∧ В)
(А ∨ В) ∧ ¬(A ∧ B)
(А ∨ В) ∧ ¬(A ∧ B)
Слайд 17
Полный одноразрядный сумматор
Должен иметь три входа (А, В
и Р0) и два выхода (S и P)
0
0
0
1
0
1
1
1
0
1
1
0
1
0
0
1
Слайд 18
Формула полного
одноразрядного сумматора
Р принимает значение 1 когда
хотя бы две из трех переменных равны 1:
Р =
(А ∧ B) ∨ (A ∧ P0) ∨ (B ∧ P0)Сумма равна произведению логического сложения (А, В и Р0) на инвертированный перенос ¬Р:
S = (А ∨ В ∨ Р0) ∧ ¬Р
Это выражение справедливо во всех случаях, кроме одного, когда А, В и Р0 равны 1:
Слайд 19
Формула полного
одноразрядного сумматора
Правильное значение суммы – 1.
Для ее получения необходимо полученное выражение сложить с произведением
этих же переменных:S = (А ∨ В ∨ Р0) ∧ ¬Р ∨ (А ∧ В ∧ Р0)
Слайд 20
Многоразрядный сумматор
Построен на основе полных одноразрядных сумматоров (по
одному на каждый разряд), причем таким образом, чтобы выход
(перенос) младшего сумматора был подключен ко входу старшего сумматора
Слайд 21
Триггер
Важнейшая структурная единица оперативной памяти и регистров процессора
Состоит
