Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Методы многомерной калибровки: PCR/PLS. Многомерная калибровка Multivariate Calibration

Содержание

11:28Тема лекцииМногомерная калибровка Multivariate CalibrationАнализ многомерных данных (Хемометрика) Multivariate Data Analysis (Chemometrics)
Проекционные методы в линейном регрессионном анализе: PCR-PLSАндрей БогомоловРоссийское хемометрическое обществоМетоды многомерной калибровки: PCR/PLS 11:28Тема лекцииМногомерная калибровка Multivariate CalibrationАнализ многомерных данных (Хемометрика) Multivariate Data Analysis (Chemometrics) К вопросу о русской терминологииродной язык хемометрики - английскийтерминология за 30 лет 11:28Регрессионный анализлинейная регрессия Y = XB + EМГК - моделирование (X) Регрессия - моделирование (X,Y) Спектроскопические данные Спектры (X) Концентрации (Y) Регрессия & Калибровка“Regression is an approach for relating two sets of variables Для чего нужна калибровка?замена прямого измерения интересующего свойства, измерением другого, коррелирующего с Примеры из различных областейХИМИЯ: калибровка – инструмент №1 количественного анализаБИОЛОГИЯ: непосредственный анализ Одномерная калибровка: один компонентY = 4.4215 XUnivariate calibrationr2 = 0.999902 r2 = 0.999344Одномерная калибровка: многокомпонентная смесь 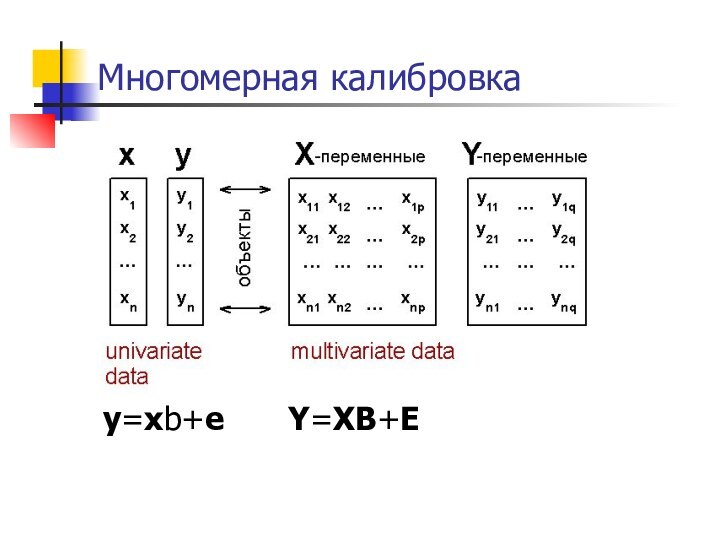Многомерная калибровкаy=xb+eY=XB+E Преимущества многомерной калибровкивозможность анализировать несколько компонентов одновременновыигрыш в точности от усреднения при Калибровка и предсказание Классические и инверсные методыДва основных подхода в многомерной калибровке: Классический МНК (Classical Множественная линейная регрессия (МЛР)Multiple Linear Regression (MLR)Решение: b = (XT X)-1 XT Недостатки МЛРМЛР может не сработать, если:высока коллинеарность в X (спектры) неустойчивое решение Пример спектральных данных: полиароматические углеводородыλ, нмε, M-1см-1[1] - 2-ацетофенантрен;[2] - 2-ацетиламинофенантрен; и 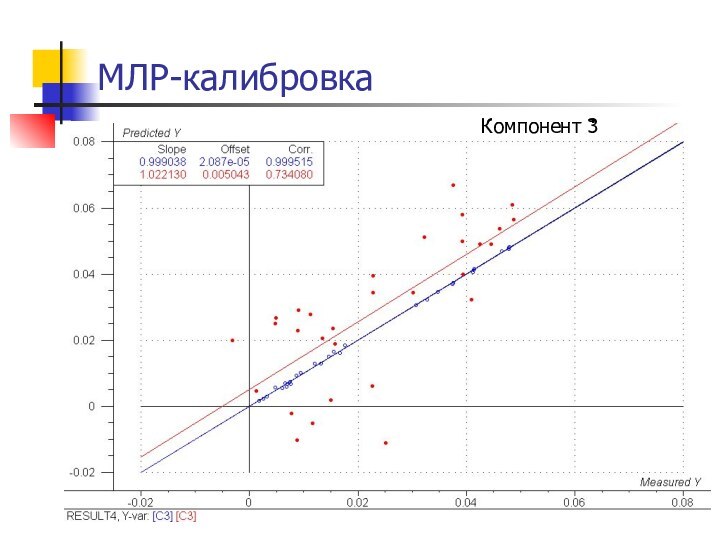МЛР-калибровка Метод главных компонент, МГК (Principle Component Analysis, PCA) преобразует данные, Концепция PCA «на пальцах» PCA + MLR = PCR !В результате РГК (PCA):Происходит компрессия данныхуменьшается размерность 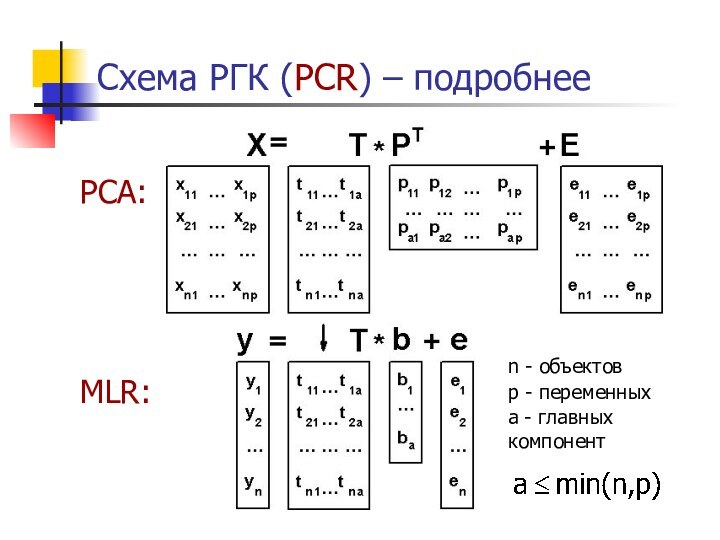Схема РГК (PCR) – подробнееPCA:MLR: Интерпретация РГК-моделиинтерпретация модели служит для изучения внутренней структуры данных:ГруппыВыбросыСвязь между X и Строим РГК-модель (Simdata) Проверка (валидация) моделипроверка (Validation) модели служит для:Определения размерности модели (числа ГК)Оценки предсказательной RMSEPRMSEС = Root Mean Square Error of CalibrationRMSEP = Root Mean Square Оценка числа компонент в РГКправильный выбор числа главных компонент - ключевая проблема 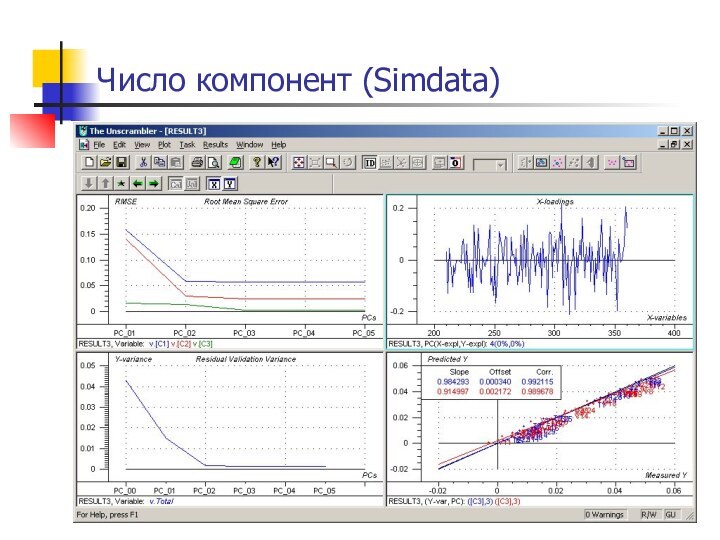Число компонент (Simdata) Оценка числа ГК в РГК: особенностичисло ГК (размерность модели) определяется нуждами калибровки, Несовершенства РГКРГК - мощный метод многомерной калибровкиимеет безусловные преимущества перед MLR однако, Факторные пространствасуществует бесконечное множество способов декомпозиции данных вида D = TPT + Eпарные PLS – мощная альтернатива PCRМетод проекции на латентные структуры (ПЛС) и ПЛС-регрессия ПЛС-регрессия: схематическое представлениеПЛС-декомпозиция затрагивает обе матрицы X и Yв результате - Две разновидности ПЛС: ПЛС1 и ПЛС2существуют две популярных разновидности ПЛС: ПЛС1 Основы алгоритма ПЛСПЛС-декомпозиция производится алгоримом NIPALSNIPALS = Non-linear Iterative Partial Least Squaresфакторы NIPALS алгоритм для ПЛС2 NIPALS алгоритм для ПЛС1 NIPALS алгоритм для ПЛС1 Предсказание по ПЛС-моделиŶ = XnewBB = W(PTW)-1QT ПЛС1 и ПЛС2ПЛС1 моделирует только одну переменную y «за раз»в этом смысле Строим ПЛС2-модель (Simdata)λ, нм Интерпретация ПЛС-моделей структура X (Simdata) Интерпретация модели служит для изучения внутренней структуры данныхСходство с РГК (PCR):X-счета и Интерпретация ПЛС-модели: выбросы (Octane)График T - U как средство детекции выбросов (outliers) Проверка ПЛС-моделей Проверка (Validation) модели преследует две основные цели:Оценка предсказательной способности модели:График “предсказанние Сравнение моделей (Simdata)Сравнение моделей калибровки трехкомпонентной смеси ПАУ (Simdata)вывод: модели РГК, ПЛС1-Р, Сравнение методов калибровкиMLR плохо пригоден для спектроскопических данныхPCR имеет недостатки, но хорошо Предсказание: диагностика соответствия новых образцовс построением калибровочной модели проблемы еще не кончаютсявозможность Диагностика предсказания (Simdata) Принципы построения «хорошей» калибровкиправильно приготовить (собрать) образцывизуально изучить данные, если необходимо, применить План семинараПример 1. Концентрационная калибровка трехкомпонентной смеси ПАУ по спектрам в УФ-видимой Рекомендуемая литератураRichard Kramer Chemometric Tchniques for Quantitative Analysis *Kim H. Esbensen Multivariate Data Пример 1: Калибровка смеси ПАУ Цель: выработка навыков калибровки с программой Unscramblerизучить Пример 2: Определение октанового числа бензина стр. 139, файл Octane Цель: работа с реальными Пример 3: Качество пшеницы стр. 150, файл Wheat Цель: самостоятельное построение калибровочной моделипостроение моделей
Слайды презентации

Слайд 2 11:28
Тема лекции

Многомерная калибровка
Multivariate Calibration

Анализ многомерных данных (Хемометрика)

11:28Тема лекцииМногомерная калибровка Multivariate CalibrationАнализ многомерных данных (Хемометрика) Multivariate Data Analysis (Chemometrics)


Multivariate Data Analysis (Chemometrics)

Слайд 3 К вопросу о русской терминологии
родной язык хемометрики -

К вопросу о русской терминологииродной язык хемометрики - английскийтерминология за 30

английский
терминология за 30 лет устоялась: статьи, учебники, книги, конференции
устоявшиеся

аббревиатуры: PCA, PCR, PLS, SIMCA, RMSEP, etc. - не нуждаются в расшифровке
русская терминология создается сейчас
почему нужен перевод?
в настоящей лекции - параллельная терминология

Слайд 4 11:28
Регрессионный анализ
линейная регрессия
Y = XB + E
МГК

11:28Регрессионный анализлинейная регрессия Y = XB + EМГК - моделирование (X) Регрессия - моделирование (X,Y)

- моделирование (X)
Регрессия - моделирование (X,Y)

Слайд 5 Спектроскопические данные
Спектры (X)
Концентрации (Y)

Спектроскопические данные Спектры (X) Концентрации (Y)

Слайд 6 Регрессия & Калибровка
“Regression is an approach for relating

Регрессия & Калибровка“Regression is an approach for relating two sets of

two sets of variables to each other” Kim Esbensen
“Calibration

is a process of constructing a mathematical model to relate the output of an instrument to properties of samples” Kenneth Beebe

Калибровка ~ Регрессия

Слайд 7 Для чего нужна калибровка?
замена прямого измерения интересующего свойства,

Для чего нужна калибровка?замена прямого измерения интересующего свойства, измерением другого, коррелирующего

измерением другого, коррелирующего с первым
такая потребность возникает если прямое

измерение интересующего свойства нежелательно:
дорого
трудоемко
занимает много времени
этически нежелательно
эксперимент невозможен, и т. п.
в подавляющем числе практических ситуаций такая замена оправдана!

Слайд 8 Примеры из различных областей
ХИМИЯ: калибровка – инструмент №1

Примеры из различных областейХИМИЯ: калибровка – инструмент №1 количественного анализаБИОЛОГИЯ: непосредственный

количественного анализа
БИОЛОГИЯ: непосредственный анализ может быть губителен для живых

существ
МЕДИЦИНА: неинвазивный анализ, например, определение сахара в крови спектроскопически (ближний ИК)
ПСИХОЛОГИЯ: анализ личности может потребовать длительных наблюдений, желательно использовать косвенные данные
СОЦИОЛОГИЯ и ФИНАНСЫ: предсказание может быть основано только на исторических данных

Слайд 9 Одномерная калибровка: один компонент
Y = 4.4215 X
Univariate calibration
r2

Одномерная калибровка: один компонентY = 4.4215 XUnivariate calibrationr2 = 0.999902

= 0.999902

Слайд 10 r2 = 0.999344

Одномерная калибровка: многокомпонентная смесь

r2 = 0.999344Одномерная калибровка: многокомпонентная смесь

Слайд 11 Многомерная калибровка

y=xb+e
Y=XB+E

Многомерная калибровкаy=xb+eY=XB+E

Слайд 12 Преимущества многомерной калибровки
возможность анализировать несколько компонентов одновременно
выигрыш в

Преимущества многомерной калибровкивозможность анализировать несколько компонентов одновременновыигрыш в точности от усреднения

точности от усреднения при использования «избыточных», в т.ч. сильно

коррелирующих измерений (спектры);
возможность диагностики «плохих» образцов в процессе предсказания
«парадигматический сдвиг» в подходах к решению проблем (например, NIR)

Слайд 13 Калибровка и предсказание

Калибровка и предсказание

Слайд 14 Классические и инверсные методы
Два основных подхода в многомерной

Классические и инверсные методыДва основных подхода в многомерной калибровке: Классический МНК

калибровке:
Классический МНК (Classical Least Squares, CLS) основан на

прямом решении уравнения Бугера-Ламберта-Бера
A = Cε | X = Yε
Инверсный МНК (Inverse Least Squares, ILS) решают уравнение вида
С = Ab | Y = Xb
В настоящей лекции – только ILS

Слайд 15 Множественная линейная регрессия (МЛР)
Multiple Linear Regression (MLR)
Решение: b

Множественная линейная регрессия (МЛР)Multiple Linear Regression (MLR)Решение: b = (XT X)-1

= (XT X)-1 XT y

y=b0 + b1x1 + b2x2+…+bpxp+e

Слайд 16 Недостатки МЛР
МЛР может не сработать, если:
высока коллинеарность в

Недостатки МЛРМЛР может не сработать, если:высока коллинеарность в X (спектры) неустойчивое

X (спектры)
неустойчивое решение для коллинеарных даных обусловлено преобразованием

(XT X)-1 XT
высокий уровень шума, ошибки в X
переменных больше, чем образцов (типично для спектральных данных)
есть линейная зависимость между переменными внутри X
визуальная интерпретация МЛР-моделей затруднительна

Слайд 17 Пример спектральных данных: полиароматические углеводороды
λ, нм
ε, M-1см-1
[1] - 2-ацетофенантрен;
[2]

Пример спектральных данных: полиароматические углеводородыλ, нмε, M-1см-1[1] - 2-ацетофенантрен;[2] - 2-ацетиламинофенантрен;

- 2-ацетиламинофенантрен; и
[3] - 3-ацетиламинофенантрен
[C1] : 0 -

1 M
[C2] : 0 - 0.5 M
[C3] : 0 - 0.05 M

C • ε + E = D

R.S.D. (E) = 0.001

Ce = C + 5% (Cmax)

Слайд 18 МЛР-калибровка

МЛР-калибровка

Слайд 19 Метод главных компонент, МГК (Principle Component

Метод главных компонент, МГК (Principle Component Analysis, PCA) преобразует данные,

Analysis, PCA) преобразует данные, проецируя их в пространство ГК
МГК

(PCA) - оружие против коллинеарности

D = TPT + E

Слайд 20 Концепция PCA «на пальцах»

Концепция PCA «на пальцах»

Слайд 21 PCA + MLR = PCR !
В результате РГК

PCA + MLR = PCR !В результате РГК (PCA):Происходит компрессия данныхуменьшается

(PCA):
Происходит компрессия данных
уменьшается размерность данных
коллинеарность обращается во благо;
уменьшается ошибка;
РГК-нагрузки

(PCA-scores) T ортогональны
содержат информацию о концентрациях компонентов
T можно использовать для построения MLR-модели, вместо X; этот метод называется…
регрессия на главные компоненты, РГК (Principal Component Regression, PCR)

Слайд 22 Схема РГК (PCR) – подробнее
PCA:
MLR:

Схема РГК (PCR) – подробнееPCA:MLR:

Слайд 23 Интерпретация РГК-модели
интерпретация модели служит для изучения внутренней структуры

Интерпретация РГК-моделиинтерпретация модели служит для изучения внутренней структуры данных:ГруппыВыбросыСвязь между X

данных:
Группы
Выбросы
Связь между X и Y
инструменты диагностики МГК (PCA) работают

в РГК (PCR):
График счетов (Scores)
График нагрузок (Loadings)
График счетов и нагрузок вместе (Bi-plot)
График остатков (Residuals)
инструменты диагностики РГК:
Совместный график нагрузок X и Y

Слайд 24 Строим РГК-модель (Simdata)

Строим РГК-модель (Simdata)

Слайд 25 Проверка (валидация) модели
проверка (Validation) модели служит для:
Определения размерности

Проверка (валидация) моделипроверка (Validation) модели служит для:Определения размерности модели (числа ГК)Оценки

модели (числа ГК)
Оценки предсказательной способности модели
проверка модели производится с

помощью тестовых данных:
того же диапазона и того же качества что обущающие данные (та же генеральная выборка)
достаточно представительные
или кросс-валидации (Cross-Validation)
Полная
Сегментная

Слайд 26 RMSEP
RMSEС = Root Mean Square Error of Calibration



RMSEP

RMSEPRMSEС = Root Mean Square Error of CalibrationRMSEP = Root Mean

= Root Mean Square Error of Prediction



минимум на

кривой RMSEP - основной индикатор числа ГК
RMSEP - оценка точности в единицах измерения!
RMSEP используется для сравнения моделей

Слайд 27 Оценка числа компонент в РГК
правильный выбор числа главных

Оценка числа компонент в РГКправильный выбор числа главных компонент - ключевая

компонент - ключевая проблема многомерной калибровки
модель с недостаточным числом

ГК (underfitting) не использует всей полезной информации из данных
модель с избыточным числом ГК (overfitting) начинает моделировать шум (ошибку)
нужно найти оптимальную размерность модели
это помогают сделать тестовые данные


Слайд 28 Число компонент (Simdata)

Число компонент (Simdata)

Слайд 29 Оценка числа ГК в РГК: особенности
число ГК (размерность

Оценка числа ГК в РГК: особенностичисло ГК (размерность модели) определяется нуждами

модели) определяется нуждами калибровки, и не обязательно совпадает с

результатом МГК
активно используется тестовые данные (Test Set)
RMSEP = Root Mean Square Error of Prediction
минимум на кривой RMSEP - основной индикатор числа ГК
для спектральных данных показательной может быть форма X-нагрузок (X-loadings)
решение всегда за экспертом!

Слайд 30 Несовершенства РГК
РГК - мощный метод многомерной калибровки
имеет безусловные

Несовершенства РГКРГК - мощный метод многомерной калибровкиимеет безусловные преимущества перед MLR

преимущества перед MLR
однако, не вполне оптимизирован для калибровки


пространство ГК оптимально для моделирования внутренней структуры данных матрицы X, но не учитывает структуры Y и связи между X и Y
можно ли учесть эту связь при построении проекционной модели?
да, использовать PLS!

Слайд 31 Факторные пространства
существует бесконечное множество способов декомпозиции данных вида
D

Факторные пространствасуществует бесконечное множество способов декомпозиции данных вида D = TPT +

= TPT + E
парные вектора в T и P

называются факторами (factors), а преобразование - проекцией данных на факторное пространство (factor space) или факторной компрессией
пространство главных компонент один из наиболее важных вариантов факторного пространства
для задания факторного пространства нужен критерий, например, МГК (PCA) использует критерий максимальной остаточной дисперсии

Слайд 32 PLS – мощная альтернатива PCR
Метод проекции на латентные

PLS – мощная альтернатива PCRМетод проекции на латентные структуры (ПЛС) и

структуры (ПЛС) и ПЛС-регрессия (ПЛС-Р)
PLS = Partial Least Squares

->
Projection on Latent Structures
ПЛС-пространство создается при участии двух переменных X и Y одновременно; критерием является моделирование той структуры (информации) в X, которая имеет корреляцию с Y
например, спектральные полосы (X), которые отвечают за концентрацию компонента(ов), заданные в Y
ПЛС-модель специально оптимизирована для регрессионного анализа

Слайд 33 ПЛС-регрессия: схематическое представление
ПЛС-декомпозиция затрагивает обе матрицы X и

ПЛС-регрессия: схематическое представлениеПЛС-декомпозиция затрагивает обе матрицы X и Yв результате -

Y
в результате - 2 набора счетов (scores) и нагрузок

(loadings)
плюс дополнительная матрица взвешенных нагрузок W (loading-weights)
критерий: максимальная ковариация между T и U

X = TPT + E
Y = UQT + F

Слайд 34 Две разновидности ПЛС: ПЛС1 и ПЛС2
существуют две популярных

Две разновидности ПЛС: ПЛС1 и ПЛС2существуют две популярных разновидности ПЛС: ПЛС1

разновидности ПЛС: ПЛС1 (PLS1) и ПЛС2 (PLS2)
ПЛС1 модель строится

для единственной переменной Y (аналогия с МЛР), например, для концентрации одного компонента смеси
если нужна калибровка по нескольким компонентам, строится несколько независимых моделей
ПЛС2 рассчитывается для нескольких компонентов одновременно
расчетные алгоритмы методов отличаются соответственно

Слайд 35 Основы алгоритма ПЛС
ПЛС-декомпозиция производится алгоримом NIPALS
NIPALS = Non-linear

Основы алгоритма ПЛСПЛС-декомпозиция производится алгоримом NIPALSNIPALS = Non-linear Iterative Partial Least

Iterative Partial Least Squares
факторы находятся по очереди, один за

другим, расчет всех факторов (как в SVD) не обязателен
итерационная замена векторов uf -> tf и uf -> tf для нахождения текущего фактора f - алгоритмическая основа ПЛС
алгоритм работает до выполнения критерия сходимости
детальное изучение алгоритмов не входит в задачу данной лекции, однако…
ознакомимся с основными шагами на примере ПЛС2

Слайд 36 NIPALS алгоритм для ПЛС2

NIPALS алгоритм для ПЛС2

Слайд 37 NIPALS алгоритм для ПЛС1

NIPALS алгоритм для ПЛС1

Слайд 38 NIPALS алгоритм для ПЛС1

NIPALS алгоритм для ПЛС1

Слайд 39 Предсказание по ПЛС-модели
Ŷ = XnewB
B = W(PTW)-1QT

Предсказание по ПЛС-моделиŶ = XnewBB = W(PTW)-1QT

Слайд 40 ПЛС1 и ПЛС2
ПЛС1 моделирует только одну переменную y

ПЛС1 и ПЛС2ПЛС1 моделирует только одну переменную y «за раз»в этом

«за раз»
в этом смысле ПЛС2 кажется гибче при калибровке

нескольких свойств, позволяя моделировать любую комбинацию переменных без их разделения - совместно
однако, ПЛС1 дает по отдельной модели на каждое из интересующих свойств, возможно, с различным числом факторов
не будет ли набор независимых моделей всегда лучшим решением?
однозначного ответа пока нет…
сравним методы на практике!

Слайд 41 Строим ПЛС2-модель (Simdata)
λ, нм

Строим ПЛС2-модель (Simdata)λ, нм

Слайд 42 Интерпретация ПЛС-моделей структура X (Simdata)

Интерпретация ПЛС-моделей структура X (Simdata)

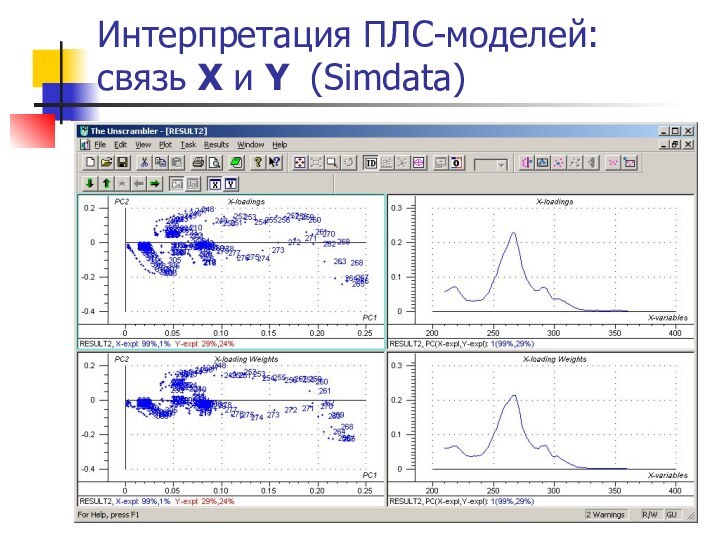
Слайд 43 Интерпретация модели служит для изучения внутренней структуры данных
Сходство

Интерпретация модели служит для изучения внутренней структуры данныхСходство с РГК (PCR):X-счета

с РГК (PCR):
X-счета и нагрузки (scores & loadings)
Особенности:
график t

– u : метод обнаружения выбросов (outliers)
графики нагрузок w – w : карта переменных
cравнение двух X-нагрузок p – w : насколько Y повлияла на декомпозицию X
график w – q

Интерпретация ПЛС-моделей: связь X и Y (Simdata)

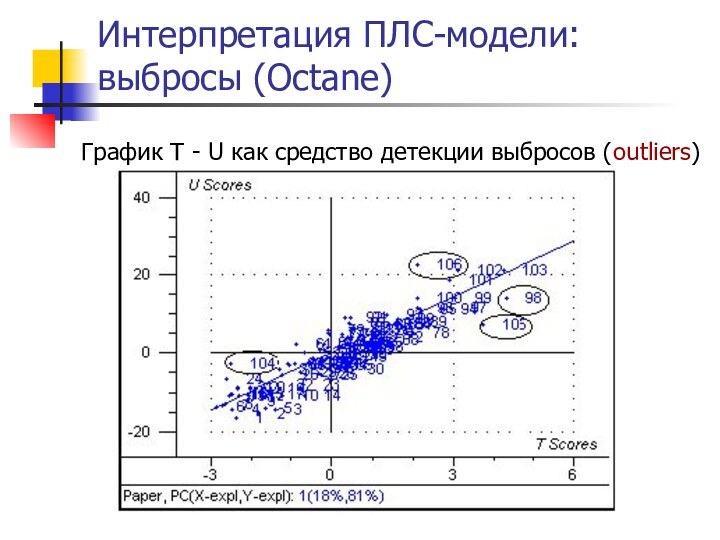
Слайд 44 Интерпретация ПЛС-модели: выбросы (Octane)

График T - U как средство

Интерпретация ПЛС-модели: выбросы (Octane)График T - U как средство детекции выбросов (outliers)

детекции выбросов (outliers)

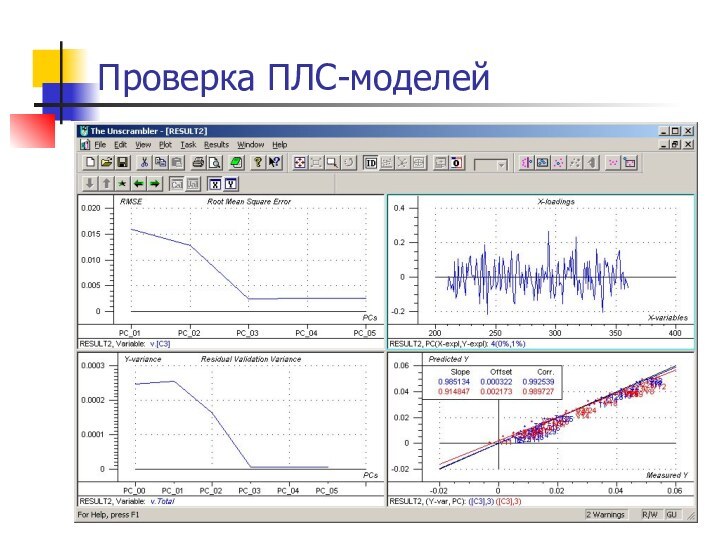
Слайд 45 Проверка ПЛС-моделей
Проверка (Validation) модели преследует две основные цели:
Оценка

Проверка ПЛС-моделей Проверка (Validation) модели преследует две основные цели:Оценка предсказательной способности модели:График

предсказательной способности модели:
График “предсказанние относительно измерения” (Predicted vs Measured)
RMSEP


Определение оптимального числа компонент
Меньше факторов чем в РГК
Минимум RMSEP

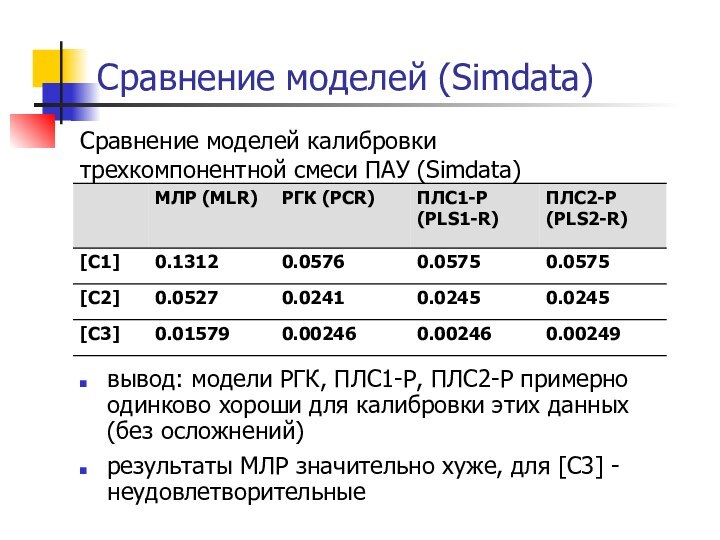
Слайд 46 Сравнение моделей (Simdata)
Сравнение моделей калибровки трехкомпонентной смеси ПАУ

Сравнение моделей (Simdata)Сравнение моделей калибровки трехкомпонентной смеси ПАУ (Simdata)вывод: модели РГК,

(Simdata)
вывод: модели РГК, ПЛС1-Р, ПЛС2-Р примерно одинково хороши для

калибровки этих данных (без осложнений)
результаты МЛР значительно хуже, для [C3] - неудовлетворительные

Слайд 47 Сравнение методов калибровки
MLR плохо пригоден для спектроскопических данных
PCR

Сравнение методов калибровкиMLR плохо пригоден для спектроскопических данныхPCR имеет недостатки, но

имеет недостатки, но хорошо работает при отсутствии осложнений
PLS является

лучшим решением для большинства практических задач
PLS1 или PLS2?
Как выбрать метод? – пробовать!
Как сравнивать разные модели? RMSEP

Слайд 48 Предсказание: диагностика соответствия новых образцов
с построением калибровочной модели

Предсказание: диагностика соответствия новых образцовс построением калибровочной модели проблемы еще не

проблемы еще не кончаются
возможность выявления образцов, несоответствующих данной регрессионной

модели является одним из преимуществ многомерного подхода в калибровке
Deviation - эмпирический параметр, характеризующий меру соответствия нового образца калибровочной модели
рассмотрим наш пример…

Слайд 49 Диагностика предсказания (Simdata)

Диагностика предсказания (Simdata)

Слайд 50 Принципы построения «хорошей» калибровки
правильно приготовить (собрать) образцы
визуально изучить

Принципы построения «хорошей» калибровкиправильно приготовить (собрать) образцывизуально изучить данные, если необходимо,

данные, если необходимо, применить предварительную обработку данных (preprocessing)
если необходимо

применить шкалирование/ взвешивание (scaling/weighting)
интерпретировать модель, изучить структуру данных, выявить и удалить возможные выбросы
тщательно оценить размерность модели, диагностировать модель
диагностировать предсказание

Слайд 51 План семинара
Пример 1. Концентрационная калибровка трехкомпонентной смеси ПАУ

План семинараПример 1. Концентрационная калибровка трехкомпонентной смеси ПАУ по спектрам в

по спектрам в УФ-видимой области (искусственные данные).
общие навыки калибровки,

интерпретации и диагностики модели, предсказания на «идеальных» данных
Пример 2. Определение октанового числа топлива по спектрам ближнего ИК.
калибровка на реальных данных, обнаружение и удаление выбросов
Пример 3. Качество пшеницы (факультативно).
самостоятельное построение калибровки, MSC, выбор переменных

Слайд 52 Рекомендуемая литература
Richard Kramer
Chemometric Tchniques for Quantitative Analysis

Рекомендуемая литератураRichard Kramer Chemometric Tchniques for Quantitative Analysis *Kim H. Esbensen Multivariate

*
Kim H. Esbensen
Multivariate Data Analysis - in Practice **
Kenneth

R. Beebee et al.
Chemometrics: a Practical Guide **
Harald Martens, Tormod Naes
Multivariate Calibration **
Richard G. Brereton
Chemometrics: Data Analysis for the Laboratory and Chemical Plant ***
Edmund R. Malinowski
Factor Analysis in Chemistry ****

Слайд 53 Пример 1: Калибровка смеси ПАУ
Цель: выработка навыков калибровки

Пример 1: Калибровка смеси ПАУ Цель: выработка навыков калибровки с программой Unscramblerизучить

с программой Unscrambler
изучить наборы данные: обучающий, тестовый, «unknown» -

в таблице, как серии спектров
построить калибровки: РГК, ПЛС2 - сравнить модели
построить ПЛС1 для каждого из 3-х компонентов, определить размерность моделей
изучить графики scores, loadings, T-U, Predicted vs Measured, RMSEP, Variance для [С1] - [С3] с разным количеством факторов
предсказать «неизвестные» образцы

Слайд 54 Пример 2: Определение октанового числа бензина
стр. 139, файл

Пример 2: Определение октанового числа бензина стр. 139, файл Octane Цель: работа с

Octane
Цель: работа с реальными данными, диагностика и устранение выбросов
преимущественно

по книге:
построить калибровку ПЛС1, диагностировать
определить выбросы, удалить, обносить калибровку
проверить модель различными способами, включая тестовый набор
построить РГК, сравнить модели
предсказать «неизвестные» образцы
  • Имя файла: metody-mnogomernoy-kalibrovki-pcrpls-mnogomernaya-kalibrovka-multivariate-calibration.pptx
  • Количество просмотров: 147
  • Количество скачиваний: 0
- Предыдущая Среда моделирования Rational Rose
Следующая - Антикризисное управление. Кризисы социально-экономических систем. (Тема 2)

Похожие презентации

Структурное, модульное программирование Структурное, модульное программирование 122
Компьютерные вирусы и антивирусные программы Компьютерные вирусы и антивирусные программы 128
Экспертные системы Экспертные системы 235
Электронная почта Электронная почта 151
Презентация к уроку информатики 11 клас Операционная система Презентация к уроку информатики 11 клас Операционная система 140
Субд Субд 196
Viegla reģistrācija Viegla reģistrācija 99
Влияние сотового телефона Влияние сотового телефона 129
Презентация по информатике на тему: Объединение ячеек в таблицах html Презентация по информатике на тему: Объединение ячеек в таблицах html 136
Презентация для объяснения нового материала по информатике на тему Компьютер - универсальная машина для работы с информацией Презентация для объяснения нового материала по информатике на тему Компьютер - универсальная машина для работы с информацией 132
СРАВНЕНИЕ МНОЖЕСТВ СРАВНЕНИЕ МНОЖЕСТВ 127
Особенности Windows 7 Особенности Windows 7 100
Презентация Электронные таблицы. Основные понятия электронных таблиц Презентация Электронные таблицы. Основные понятия электронных таблиц 170
Технологии проектирования компьютерных систем. Представление системы в VHDL. (Лекция 7) Технологии проектирования компьютерных систем. Представление системы в VHDL. (Лекция 7) 118
Человек и компьютер Человек и компьютер 104
Аттестационная работа. Элективный курс по информатике Математические основы информатики Аттестационная работа. Элективный курс по информатике Математические основы информатики 108
CRM-системы CRM-системы 196
Презентация по информатике Устройства ввода Презентация по информатике Устройства ввода 127
Как вставить видео Как вставить видео 155
Обнаружение сетевых атак Обнаружение сетевых атак 137
Компьютерные сети Компьютерные сети 146
Computer Programming Essentials| Java | Java Technologies Computer Programming Essentials| Java | Java Technologies 127
Схема Схема 133
Типы алгоритмов Типы алгоритмов 124
Администрирование почтовых серверов Администрирование почтовых серверов 115
Устройства ввода и вывода информации Устройства ввода и вывода информации 127
Интерактивная игра по информатике Своя игра тренажёр по информатике Интерактивная игра по информатике Своя игра тренажёр по информатике 261
Разработка программного обеспечения для мобильного информационного робота Разработка программного обеспечения для мобильного информационного робота 122
Интерфейс пакета Microsoft Office 2010 Интерфейс пакета Microsoft Office 2010 155
Пересечение и объединение множеств Пересечение и объединение множеств 150