Слайды
1. Общие понятия. Первая программа 3
2. Запись математических выражений 27
3. Условный
оператор if ... else 41
4. Циклы. Конструкция циклов 60
5. Отладка программы 83
6. Массивы 90
7. Оператор switch 101
8. Функция (подпрограмма) 107
9. Файловый ввод/вывод 125
10. Построение графиков (C++ & Excel) 130
11. Задания для самостоятельной работы 147
12. Технические приложения 162
13. Литература 167
Слайд 4
Массив (совокупность нескольких значений) Имя массива создается аналогично
имени обычной переменной, но за именем массива в квадратных
скобках указывается количество элементов массива, которое задается при его объявлении. Чтобы описать элементы массива сразу при его создании, можно использовать фигурные скобки. В фигурных скобках значения элементов массива перечисляются через запятую. В конце закрывающей фигурной скобки ставится точка с запятой. При объявлении массива нумерация элементов массива начинается с нуля. Массив, как и любую переменную можно не заполнять значениями при объявлении.
Описание массива и вывод на печать
Слайд 5
#include
using namespace std;
int main()
{
setlocale (0, "");
int a[5]={5,10,15,20,25};
for
(int i=0; i
a[i] << endl;
return 0;
}
Пример 27 (вариант заполнения массива сразу после его объявления)
Важно: нумерация элементов массива начинается с 0:
a[0] = 5
a[1] = 10
a[2] = 15
a[3] = 20
a[4] = 25
Элемента a[5] не существует .
5
элементов
Слайд 6
Пример 28 (вариант заполнения массива с помощью оператора
цикла)
#include
using namespace std;
int main()
{
setlocale (0, "");
int a[7];
for (int
i=0; i < 7; i++)
{
if (i==0)
a[i]=1;
else
a[i] = a[i-1]*2;
cout << a[i] << endl;
}
return 0;
}
Слайд 7
Написать программы, аналогичные примеру 27 на заполнение массива
при объявлении. Вывести массивы на монитор:
P[7]=0, -1, 1, -2,
2, -3, 3;
Q[8]=1.8, 2.5, 3.7, 4.9, 2.9, 1.5, -1.7, -2.3;
R[4]=3, 33, 333, 3333;
Написать программы, аналогичные примеру 28 на заполнение массива с помощью оператора цикла. Вывести массивы на монитор:
S[5]=1, 10, 100, 1000, 10000;
T[5]=-1, -8, -27, -64, -125;
U[6]=1.5, 2.0, 2.5, 3.0, 3.5, 4.0;
Слайд 8
Пример 29. Написать программу для вычисления дальности полета
тела, брошенного под углом α к горизонту. Сопротивлением воздуха
пренебречь. Расчет провести для следующих углов бросания: 0, 15, 30, 45, 60, 75, 90 градусов. Для хранения рассчитанных значений дальности создать массив L[7]. Задать начальную скорость бросания равной V = 20 м/сек. Ускорение свободного падения g = 9,81 м/сек2 .
Дальность полета тела рассчитывается по формуле
Слайд 9
#include
#include
using namespace std;
double v=20;
double g=9.81;
double pi=3.1416;
double
alf;
double L[7];
int main()
{
setlocale (0, "");
alf=0;
int i;
for (i=0; i
<< alf << " " << L[i] << endl;
alf=alf+pi/12;
}
return 0;
}
Пример 29
Слайд 10
Пример 30.
Взять за основу программу предыдущего примера
и видоизменить ее так, чтобы начальная скорость и угол
бросания вводились с клавиатуры. Тогда программа будет находить дальность полета при любой начальной скорости и любом угле бросания, заданных с клавиатуры. Вывести на монитор заданный угол бросания, заданную начальную скорость и рассчитанную дальность полета.
Примечание: угол вводить в градусах, а в формулу подставлять в радианах.
Слайд 11
#include
#include
using namespace std;
double v, alf, L;
double
g=9.81;
double pi=3.1416;
int main()
{
setlocale (0, "");
cout
>> v;
cout << "Введите угол: ";
cin >> alf;
alf=alf*pi/180;
L=2*pow(v,2)*sin(alf)*cos(alf)/g;
cout << "Дальность полета: " << L << endl;
return 0;
}
Пример 30
Слайд 12
Пример 31.
Написать программу для перевода двоичного числа в
десятичное.
Использовать следующий алгоритм
где b – десятичное число;
an – крайняя
слева цифра двоичного числа;
n – количество цифр в двоичном числе.
Например, перевести двоичное число 11001011 в десятичное:
При написании программы представить двоичное число в виде массива a[8] = {1,1,0,0,1,0,1,1}
Слайд 13
#include
#include
using namespace std;
int main()
{
int
i;
int b=0;
int a[8]={1,1,0,0,1,0,1,1};
for (i=0; i
endl;
return 0;
}
Пример 31
Слайд 15
Оператор SWITCH
Конструкция оператора
switch:
switch (переключатель) {
case
значение1:
инструкция1;
break;
case значение2:
инструкция2;
break;
…
}
Пример,
a=2;
switch (a)
{
case 1:
b=1;
break;
case 2:
b=2;
break;
}
В качестве переключателя могут выступать только целочисленные переменные или выражения.
Слайд 16
Пример 32. Вывод словесного описания оценки, основываясь на
текущей оценке ученика
#include
using namespace std;
int main() {
setlocale
(0, "");
int grade;
cout << "Введите оценку от 2 до 5" << endl;
cin >> grade;
switch (grade)
{ case 5: cout << "У вас оценка отлично" << endl; break;
case 4: cout << "У вас оценка хорошо" << endl; break;
case 3: cout << "У вас всего лишь удовлетворительно" << endl; break;
case 2: cout << "Плохо, у вас двойка" << endl; break;
}
return 0;
}
Использование оператора SWITCH
Слайд 17
Написать программу – калькулятор, которая будет выполнять для
двух чисел a, b, введенных с клавиатуры, следующие математические
операции:
1. a+b;
2. a-b;
3. a*b;
4. a/b;
Пример 33
>> a;
cout
>> b;
cout << "Выберите действие: " << endl;
cout << "1. Сложить a+b" << endl;
cout << "2. Вычесть a-b" << endl;
cout << "3. Умножить a*b" << endl;
cout << "4. Разделить a/b" << endl;
cin >> z;
switch (z)
{
case 1: cout << "a+b= " << a+b << endl;
break;
case 2: cout << "a-b= " << a-b << endl;
break;
case 3: cout << "a*b= " << a*b << endl;
break;
case 4: cout << "a/b= " << a/b << endl;
break;
}
Пример 33. Дописать программу.
Слайд 19
Пример 34.
Дополнить пример 33 следующими математическими операциями:
5. b-a;
6.
b/a;
7. sqrt (a);
8. sqrt (b);
Слайд 21
Функция (в Fortran – процедура) –
подпрограмма , выполняющая действия, многократно повторяющиеся в основной программе.
Использование функций сокращает объем программы и уменьшает вероятность появления ошибок в программе.
Функция может иметь возвращаемое значение или не иметь возвращаемого значения.
Функция может быть с параметрами или без параметров. В функции без параметров не указывается возвращаемое значение. Начинается с оператора void.
Код функции может быть размещен в начале программы или в конце программы. Во втором случае в начале программы необходимо объявить функцию с помощью оператора, который называется прототипом функции. При этом описание прототипа не отличается от описания заголовка функции.
Функция (подпрограмма)
Слайд 22
INT
LONG
DOUBLE
В списке параметров перед каждым параметром
указывается тип, параметры разделяются запятыми.
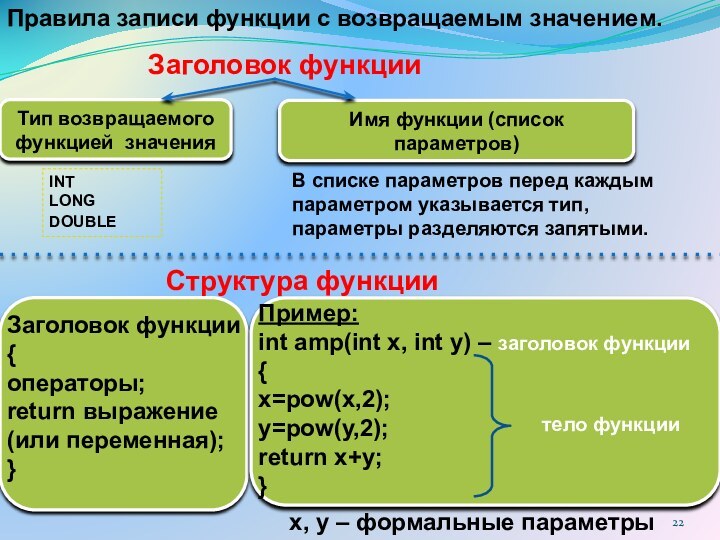
Структура функции
Заголовок функции
{
операторы;
return выражение (или
переменная);
}
Пример:
int amp(int x, int y) – заголовок функции
{
x=pow(x,2);
y=pow(y,2);
return x+y;
}
Тип возвращаемого функцией значения
Имя функции (список параметров)
Заголовок функции
Правила записи функции с возвращаемым значением.
x, y – формальные параметры
тело функции
Слайд 23
Функция состоит из заголовка и тела функции. Тело
функции заключается в фигурные скобки. В прототипе и теле
функции задаются формальные параметры. Внутри функции они доступны как локальные переменные.
Фактические параметры существуют в основной программе. Они указываются при вызове функции на месте формальных. В момент вызова функции значения фактических параметров присваиваются формальным параметрам. Имена формальных и фактических параметров могут совпадать, это не вызовет конфликта.
Не рекомендуется создавать функции, обращающиеся к глобальным переменным, так как в этом случае функция становится привязанной к конкретной основной программе.
Слайд 24
Соответствие фактических параметров формальным параметрам устанавливается в том
порядке, в котором они были объявлены. Тип фактических параметров
должен совпадать или быть совместимым с типом формальных параметров. Одна функция не может объявляться или определяться внутри другой т.е. нельзя объявлять и определять функции внутри main. Но одна функция может вызываться внутри другой. В частности, внутри своего тела функция может вызывать саму себя. Такое явление называется рекурсией.
Слайд 25
#include
#include
using namespace std;
double a, b, z1,
z2;
double amp(double x, double y); //
прототип функции «amp»
int main()
{
setlocale (0, "");
cout << "Введите a: ";
cin >> a;
cout << "Введите b: ";
cin >> b;
z1=a+b;
z2=pow(a,2)+pow(b,2);
cout << amp(z1,z2); /* z1, z2 фактические параметры, подставляемые вместо формальных параметров в функцию amp */
return 0;
}
double amp(double x, double y) // функция «amp»
{
x=x+1;
y=y+1;
return x/y; // x/y - возвращаемое значение
}
Пример 35
Задание: записать пример 35 без прототипа функции.
Слайд 26
#include
#include
using namespace std;
int x=4;
int y, yy,
z;
int aver (int a, int b) // функция
{
z=(a+b)/2;
}
int
main() {
y=pow(x,2);
aver (x,y);
cout << z << endl;
yy=pow(x,3);
aver (y,yy);
cout << z << endl;
return 0;
}
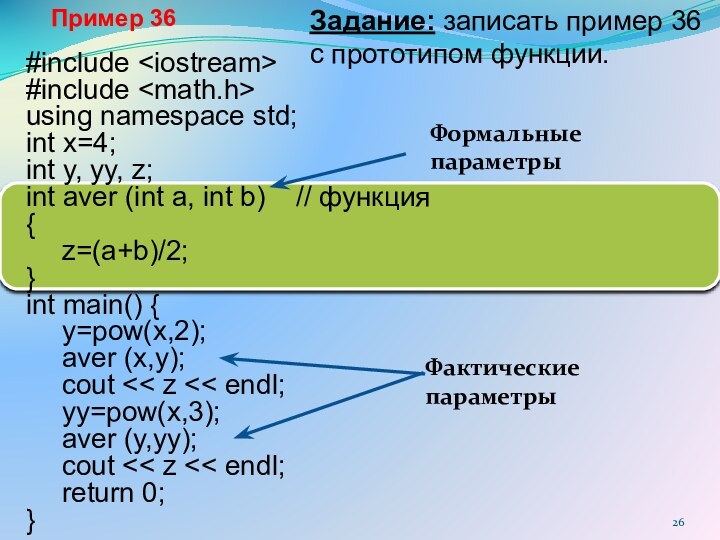
Формальные параметры
Фактические
параметры
Пример 36
Задание: записать пример 36 с прототипом функции.
Слайд 27
Функция с параметрами
Функция без параметров
Слайд 28
Функция с возвращаемым
значением
Функция без возвращаемого
значения
Слайд 29
В рассмотренных примерах функция без возвращаемого значения avrg
становится зависимой от глобальной переменной z, что нежелательно. В
случае функции с возвращаемым значением aver такой зависимости нет, так как все переменные определены внутри функции. Переменная z в этом случае является локальной. В языке C++ локальными являются переменные объявленные внутри функции или блока, ограниченного фигурными скобками.
Слайд 30
Возвращаемых значений в
функции может быть несколько,
например,
#include
#include
using namespace std;
int x (4), y;
double z1, z2;
int
aver(int a, int b) {
z1=a+b;
z2=(a+b)/2;
return z1, z2;
}
int main() {
y=pow(x,2);
aver (x,y);
cout << z1 << " " << z2 << endl;
return 0;
}
Пример 37
Примечание: int x(4) означает int x=4;
Задание: записать пример 37
с прототипом функции.
Слайд 31
Итак, когда мы работаем с функцией, надо указать
тип возвращаемого функцией значения, имя функции, задать перечень формальных
параметров с указанием типа в круглых скобках после имени функции (точку с запятой после заголовка функции ставить не надо), записать необходимые действия в теле функции, и вернуть результат работы функции оператором return.
Оператор return заканчивает выполнение функции и возвращает управление в вызывающую функцию.
Если описание функции располагается после main, то перед main необходимо объявить прототип функции.
Правила работы с функцией (имеющей формальные параметры и возвращаемое значение)
Слайд 32
Пример 38. Необходимо найти путь и расход топлива
для автомобиля, который во время поездки двигался с различной
скоростью в течение различных временных отрезков.
Пусть скорость автомобиля описывается следующим массивом скоростей:
V[7] = {60,70,80,90,100,110,120} км/час. Этому массиву скоростей соответствует массив временных промежутков:
t[7] = {0.7, 0.65, 0.55, 0.4, 1.2, 1.0, 1.5} часов.
Путь будем определять по формуле S = V·t, а расход топлива по формуле R = 0,001·V2 ·t, где S[км], V[км/час], t[час], R[л]. Последняя формула учитывает зависимость расхода топлива не только от времени движения автомобиля, но и от его скорости. За исходную величину расхода топлива принимается расход в10 литров на 100 км пути при скорости 100 км/час. При уменьшении скорости расход топлива уменьшается, при увеличении скорости – увеличивается.
Слайд 33
#include
#include
using namespace std;
double S=0;
double R=0;
int v[7]={60,70,80,90,100,110,120};
//массив скоростей
double t[7]={0.7,0.65,0.55,0.4,1.2,1.,1.5}; /*массив временных промежутков, соответствующих массиву скоростей*/
double
F1(int a, double b); /*прототип функции для вычисления пути */
double F2(int a, double b); /*прототип функции для вычисления расхода топлива */
int main()
{
setlocale(0, "");
Пример 38 (начало)
Вместо формальных параметров a, b подставляем фактические значения скорости
и времени на i-ом отрезке пути */
R=R+F2(v[i],t[i]); //Вычисляем расход топлива
}
cout << S <<" "<< R;
return 0;
}
double F1(int a, double b) { //описание функции F1
return a*b;
}
double F2(int a, double b) { //описание функции F2
return 0.001*pow(a,2)*b;
}
Пример 38 (продолжение)
Слайд 35
Пример 38 (результаты расчета)
Задание: записать пример 38 без
прототипов функций.
Слайд 36
где L – длина маятника,
g – ускорение свободного
падения.
Получить результаты для длины L1=5 м и L2=10 м.
Для
вычисления T использовать подпрограмму-функцию.
Пример 39. Написать программу для расчета периода колебаний математического маятника.
Период колебаний математического маятника определяется по формуле:
Слайд 37
#include
#include
using namespace std;
double PF (int LM)
{
double
pi=3.1416;
double g=9.81;
double TM;
TM=2*pi*sqrt(LM/g);
return TM;
}
int main()
{
int L=5;
double T1, T2;
T1=PF(L);
cout
"T1= " << T1 << endl;
L=10;
T2=PF(L);
cout << "T2= " << T2 << endl;
return 0;
}
Пример 39
Слайд 39
Пример 40. Запись результатов вычисления функции sin(x) в
текстовый файл
#include
#include
#include
using namespace std;
double x;
double dh=3.1416/20;
int
main()
{
setlocale (LC_ALL,"Russian");
ofstream f;
f.open ("snx.txt");
for (int i=0; i<=10; i++)
{
x=dh*i;
f << sin(x) << endl;
}
return 0;
}
Слайд 40
Рассмотрим пример 40 подробнее:
#include //подключить библиотеку fstream
ofstream.f;
//output file stream – организовать поток вывода в файл,
f.open
(«snx.txt"); //открыть текстовый файл snx.txt для записи,
f << sin(x) << endl; //записать значения sin(x) в файл snx.txt
Это четыре минимально необходимых строчки кода программы, чтобы организовать вывод в файл.
Результат вывода имеет вид:
Слайд 41
Пример 41. Считывание данных из текстового файла test.txt
#include
#include
#include
using namespace std;
int main()
{
setlocale (LC_ALL,"Russian");
ifstream f;
f.open ("test.txt");
double
a[11];
for (int i=0; i<=10; i++)
{
f >> a[i];
cout << a[i] << endl;
}
return 0;
}
Слайд 42
Рассмотрим пример 41 подробнее:
#include //подключить библиотеку fstream
ifstream.f;
// input file stream – организовать поток ввода из
файла,
f.open ("test.txt"); //открыть текстовый файл test.txt,
f >> a[i]; //записать значения из файла test.txt в массив a[11]
Имеем, как и в предыдущем случае, четыре минимально необходимых строчки кода программы, чтобы организовать ввод из файла в программу.
Тестовый файл test.txt заполняем значениями синуса из предыдущего примера. Результат ввода из файла имеет вид:
Слайд 44
Иногда необходимо не просто получить результаты расчета, но
и построить график по результатам расчета. Поведение кривых на
построенном графике позволяет оперативно контролировать правильность написанной программы.
Будем проводить расчеты в С++, а график строить в Excel, поскольку Excel имеет более развитый инструментарий для построения графиков и диаграмм, нежели С++. Чтобы автоматизировать перенос результатов расчета из C++ в Excel, результаты расчетов будем выводить в файл, а затем копировать в Excel.
Слайд 45
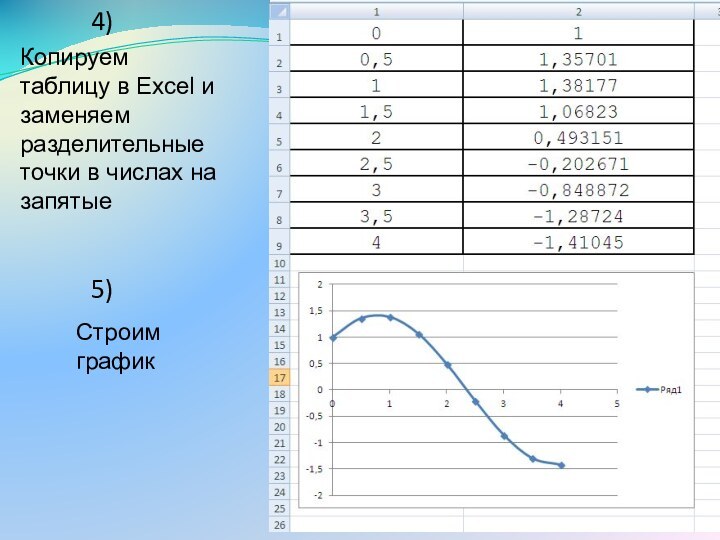
Последовательность действий при построении графика
1. Написать программу, в
которой значения аргумента и функции выводятся в файл, а
не на консоль. Предусмотреть вывод запятой между аргументом и функцией.
2. Открыть полученный файл в программе Microsoft Office Word.
3. Преобразовать данные в таблицу с помощью опций Вставка > Таблица > Преобразовать в таблицу, используя в качестве разделителя данных запятую после аргумента.
4. Скопировать таблицу в Excel и заменить точку в полученных данных на запятую с помощью опций Главная > Найти и выделить > Заменить.
5. Построить график в Excel с помощью опций Вставка > Точечная > Точечная с гладкими кривыми.
Слайд 46
Примечание. Чтобы Excel не переводил автоматически дробное число
в дату при копировании из Word в Excel, измените
системные настройки даты с «.» на «/» в Панель управления > Язык и региональные стандарты:
Слайд 47
#include
#include //библиотека потокового ввода/вывода
#include
using
namespace std;
double trig(double var); // прототип функции trig
int main()
{
setlocale
(0, "");
double a, b, h, x;
char s[20]; // строка из 20 символов для имени файла
cout << "Введите начальное и конечное значение аргумента и шаг: ";
cin >> a >> b >> h;
cout << "Введите имя файла: ";
cin >> s;
ofstream f; //объявляем поток записи в файл
f.open(s); // открываем файл
Пример 42. Построить график функции y=sin(x)+cos(x)
1)
f
файл и одновременно ставим запятую после аргумента, которая позволит нам преобразовать результаты в таблицу */
f.width(15);
f << trig(x) << endl; /*вызываем функцию с текущим аргументом х и пишем результаты вычислений в файл */
}
f.close(); // закрываем файл
return 0;
}
double trig(double var) { // функция trig
return sin(var)+cos(var);
}
Пример 42 (продолжение)
Слайд 49
2)
3)
Файл с
результатами
расчетов
Преобразовываем
результаты в
таблицу
Слайд 50
4)
5)
Строим
график
Копируем
таблицу в Excel и
заменяем
разделительные
точки в
числах на
запятые
Слайд 51
Пример 43. При подключении разряженного конденсатора C к
источнику напряжения U0 через резистор R, напряжение на конденсаторе
увеличивается от 0 до U0 по закону
Где постоянная заряда, имеющая размерность [сек].
Написать программу расчета кривой U(t) и построить график этой кривой.
Расчет проведем при следующих исходных данных: R=1 кОм, С=1000 мкФ, время окончания заряда ts=4 с, шаг по времени dt=0.1с.
Слайд 52
#include
#include
#include
using namespace std;
double u0=12;
double tau=1;
double
volt(double x); // прототип функции
int main() {
double t,
ts, dt;
setlocale (0, "");
char s[20];
cout << "Введите время окончания расчета ts: ";
cin >> ts;
cout << "Введите шаг dt: ";
cin >> dt;
cout << "Введите имя файла ";
cin >> s;
Пример 43 (начало)
Слайд 53
ofstream f; // вывод в файл
f.open(s);
// открыть файл
for (t=0; t
f.width(10);
f << t << ","; /* Записываем в файл аргумент t и одновременно пишем после него запятую */
f.width(15);
f << volt(t) << endl; /* вызываем функцию volt с текущим аргументом t и пишем результаты вычислений в файл*/
}
f.close(); //Закрываем файл
return 0;
}
double volt(double x) {
return u0*(1-exp(-x/tau));
}
Пример 43 (продолжение)
Слайд 54
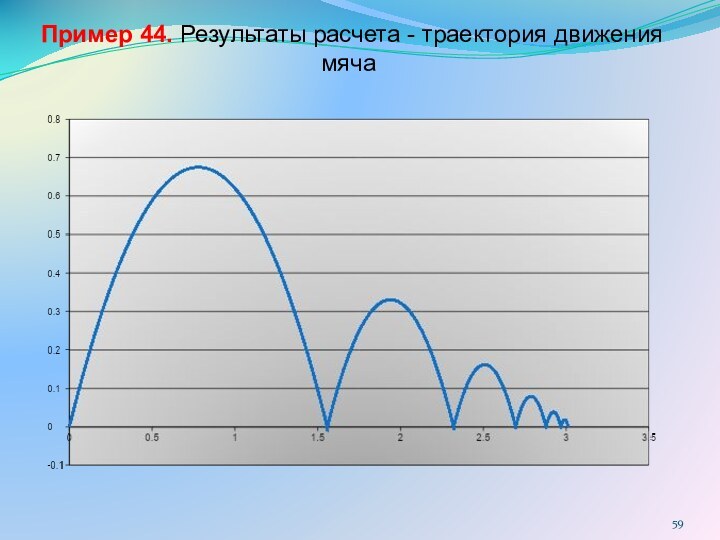
Пример 43 (построение графика)
Таблица приведена в сокращенном
виде.
Слайд 55
Мяч падает на пол в точке А со
скоростью V1=6 м/с. Угол падения мяча составляет 30 град.
от вертикали. При каждом отскоке мяч теряет 30% скорости, т.е. для скорости отскока можно записать V2=0.7*V1. Угол отскока мяча равен углу падения. При втором и каждом последующем падении мяча скорость падения равна скорости предыдущего отскока. Угол падения и угол отскока сохраняют значение 30 град.
Написать программу и вывести на монитор траекторию движения мяча при подскоках. Число отскоков задать равным 6.
Высота подъема мяча при отскоке
Время движения мяча между двумя соседними подскоками
, где - вертикальная составляющая скорости отскока.
Пример 44 (построение траектории)
Слайд 56
#include
#include
#include //библиотека для
выводы в файл
using namespace std;
double V1=6, g=9.80665, pi=3.14159;
int main()
{
setlocale(LC_ALL,
"Russian");
char s[20];
double x, t, tm, dt, V2, Vx, Vy, Vys, h;
int i, j, N;
double xp[7]; // массив координат точек подскока
double tp[7]; //время, соответствующее точкам подскока
cout << "Введите имя файла: ";
cin >> s;
ofstream f; // указываем поток вывода в файл
f.open(s); // открыть файл
tp[0]=0;
xp[0]=0;
Пример 44 (начало)
// N - число разбиений отрезка между отскоками
for (i=0;
i<=6; i=i+1) // цикл по точкам подскока
{
V2=0.7*V1;
Vy=V2*cos(pi/6);
Vx=V2*sin(pi/6);
tm=Vy/g; // время подъема на максим. высоту при отскоке
tp[i+1]=tp[i]+2*tm; //время до следующей точки отскока
xp[i+1]=xp[i]+Vx*2*tm; //расстояние до след. точки отскока
dt=2*tm/N; // шаг по времени
for (j=0; j<=N; j=j+1) /*цикл на построение траектории между соседними точками отскока */
{
if (j==0)
{
h=0;
x=xp[i];
t=tp[i];
Vys=Vy; //запоминание вертик. скорости в предыд. момент
}
Пример 44 (продолжение)
Слайд 58
else
{
Vy=Vy-g*dt;
h=h+dt*(Vy+Vys)/2; /* расчет высоты с учетом средней скорости
за промежуток времени dt */
x=x+Vx*dt;
t=t+dt;
Vys=Vy;
}
f
", "; //запись координаты х в файл
f << h << endl; //запись высоты, соответствующей коорд. х
}
V1=V2; // переприсвоение скоростей падения и отскока
cout << tp[i] << " "<< xp[i] << endl;
}
f.close(); //закрываем файл
}
Пример 44 (окончание)
Слайд 59
Пример 44. Результаты расчета - траектория движения
мяча
Слайд 61
Написать программы самостоятельно:
45. Написать программу, выводящую на монитор
элементы в диапазоне от 11 до 20 для последовательности
чисел 1 3 5 7 9 11 13 15 17 19 21 23 25
46. Написать программу, выводящую на монитор первые 5 элементов последовательности 2 4 8 16 32 64 128
47. Написать программу, вычисляющую факториал натурального числа n, которое пользователь вводит с клавиатуры (n!=1·2·3·4·…·n).
48. Написать программу, переводящую двоичные числа в десятичные:
1100011111 (ответ: 799),
11001110001 (ответ: 1649),
101010111111 (ответ: 2751).
Слайд 62
49. Уравнение идеального трансформатора имеет вид
где
- напряжение в первичной
и вторичной обмотках соответственно,
- число витков в первичной и вторичной обмотках соответственно.
Написать программу для определения напряжения во вторичной обмотке при известных значениях . Значения вводить с клавиатуры.
Слайд 63
50. Написать программу для расчета сопротивления электрической цепи
при параллельно-последовательном соединении резисторов:
Сопротивления резисторов R1 … R4 вводить
с клавиатуры.
Слайд 64
51. Написать программу для расчета сопротивления электрической цепи
при параллельно-последовательном соединении резисторов:
Сопротивления резисторов R1 … R7 вводить
с клавиатуры. Для расчета параллельного участка цепи использовать подпрограмму – функцию.
Слайд 65
52. Написать программу для расчета сопротивления электрической цепи
при параллельно-последовательном соединении резисторов:
Сопротивления резисторов R1 … R7 вводить
с клавиатуры. Для расчета параллельного участка цепи использовать подпрограмму – функцию.
Слайд 66
53. Написать программу для вычисления корней квадратного уравнения
Выражение
называется дискриминантом и обозначается буквой D. Если дискриминант больше нуля, то существуют два корня, если D=0, то существует один корень, и если D<0, то действительных корней не существует.
Коэффициенты квадратного уравнения a, b, с вводить с клавиатуры.
Корни квадратного уравнения вычисляются по формуле
Слайд 67
54. Пример на эффект Доплера. Пусть имеется источник
звукового сигнала, который излучает звук частотой f0 , и
приемник, который принимает звуковой сигнал. Частота принимаемого звука зависит от скоростей источника и приемника. Возможны случаи:
Случай 1. Источник сигнала приближается к приемнику со скоростью Vист . Тогда частота звука, принимаемого приемником, будет равна
Случай 2. Источник сигнала удаляется от приемника со скоростью Vист . Тогда частота звука, принимаемого приемником, будет равна
Слайд 68
Случай 3. Источник сигнала и приемник движутся навстречу
друг другу со скоростями соответственно Vист и Vпр .
Тогда частота звука, принимаемого приемником, будет равна
Случай 4. Источник сигнала и приемник удаляются друг от друга со скоростями Vист и Vпр . Тогда частота звука, принимаемого приемником, будет равна
Написать программу с оператором switch для вычисления частоты звука для рассмотренных случаев. Принять скорость звука V = 340 м/сек. Переменные f0 , Vист , Vпр вводить с клавиатуры.
Слайд 69
62)
61)
60)
59)
58)
57)
56)
55)
Написать программы для вычисления значения y при следующих
исходных данных:
а = 6.5, 7.0, 7.5, 8.0, 8.5,
9.0;
b = 14.3, 15.0, 15.7, 16.4, 17.1
Слайд 70
Написать программы для вычисления значения y при следующих
исходных данных:
= 10, 20, 30, 40, 50,
60 градусов,
= 15, 30, 45, 60, 75 градусов
63)
64)
65)
66)
67)
68)
Слайд 71
К примеру 63 (вар.1)
#include
#include
using namespace std;
int

i,j;
double a, b; // углы
и
double pi=3.1416;
double ar, br, y;
int main()
{
a=0;
for (i=1; i<=6; i++) // цикл по углу
{
a=a+10;
ar=(a*pi)/180; // угол в радианах
b=0;
for (j=1; j<=5; j++) // цикл по углу
{
b=b+15;
br=(b*pi)/180; // угол в радианах
y=sin(ar)+tan(br);
cout<<"a="<
Слайд 72
К примеру 63 (вар.2)
#include
#include
using namespace std;
double

a, b;
// углы и
double pi=3.1416;
double ar, br, y;
int main()
{
for (a=10; a<=60; a=a+10) // цикл по углу
{
ar=(a*pi)/180; // угол в радианах
for (b=15; b<=75; b=b+15) // цикл по углу
{
br=(b*pi)/180; // угол в радианах
y=sin(ar)+tan(br);
cout<<"a="<
Слайд 73
Мяч падает на пол в точке А со
скоростью V1=6 м/с. Угол падения мяча составляет 30 град.
от вертикали. При каждом отскоке мяч теряет в скорости 30%, т.е. скорость отскока равна V2=0.7*V1, угол отскока мяча равен углу падения. При втором и каждом последующем падении мяча скорость падения равна скорости предыдущего отскока. Угол падения и угол отскока сохраняют значение 30 град.
Написать программу и вывести на монитор максимальную высоту подъема после каждого отскока мяча и расстояние от первоначальной точки падения до текущей точки отскока. Число отскоков задать равным 6.
Высота подъема мяча при отскоке
Время движения мяча между двумя соседними подскоками
, где - вертикальная составляющая скорости отскока.
Пример 69
Слайд 74
Построить графики в диапазоне от -4 до 4
70.
71.
72.
73.
Построить
графики в диапазоне от 0 до
Слайд 76
Пример 74. Рассмотрим, как программирование может пригодиться при
создании технического устройства. Техническим устройством, в частности, может служить
прибор, управляющий подсветкой различных объектов. На фотографии представлен макет технического устройства, состоящий из микроконтроллерной платы Ардуино и линейки светодиодов.
Программирование микроконтроллерной платы осуществляется с помощью упрощенного аналога С++. Процесс программирования платы подробно описан в литературе [7]. Там же есть описания других устройств на Ардуино.
Программа, управляющая миганием светодиодов, представлена на следующих слайдах.
Слайд 77
#define S1 3
#define S2 4
#define S3 5
#define S4
6
#define S5 7
#define S6 8
#define S7 9
#define S8 10
#define
S9 11
#define S10 12
int Led[10]={S1, S2, S3, S4, S5, S6, S7, S8, S9, S10};
int i, j;
void setup()
{
for (i=0; i<=9; i++)
pinMode (Led[i], OUTPUT);
}
void loop()
{
for (i=0; i<=9; i++) // начальное обнуление
digitalWrite(Led[i],LOW);
for (j=1; j<=5; j++) //последовательное мигание светодиодов
{
Пример 74 (начало)
digitalWrite(Led[i],HIGH);
delay (70);
digitalWrite(Led[i],LOW);
}
}
for (j=1; j<=5; j++) // одновременное мигание линейки
{
for (i=0; i<=9; i++)
digitalWrite(Led[i],LOW);
delay (500);
for (i=0; i<=9; i++)
digitalWrite(Led[i],HIGH);
delay (500);
}
for (j=1; j<=5; j++) //переключение между половинами линейки
{
for (i=0; i<=4; i++)
digitalWrite(Led[i],LOW);
for (i=5; i<=9; i++)
digitalWrite(Led[i],HIGH);
delay (500);
for (i=0; i<=4; i++)
digitalWrite(Led[i],HIGH);
Пример 74 (продолжение)
digitalWrite(Led[i],LOW);
delay (500);
}
for (j=1; j<=5; j++) //мигание первой половины линейки
{
for (i=0; i<=4; i++)
digitalWrite(Led[i],HIGH);
delay (100);
for (i=0; i<=4; i++)
digitalWrite(Led[i],LOW);
delay(100);
}
for (j=1; j<=5; j++) //мигание второй половины линейки
{
for (i=5; i<=9; i++)
digitalWrite(Led[i],HIGH);
delay (100);
for (i=5; i<=9; i++)
digitalWrite(Led[i],LOW);
delay(100);
}
}
Пример 74 (окончание)








![Начальное программирование на С++. Графики. Технические приложения. Часть 2. #include #include using namespace std;double v=20;double g=9.81;double pi=3.1416;double alf;double L[7];int main(){ setlocale (0,](/img/tmb/11/1066648/b6f09f34d6dd5a4d65e584dedec02ca7-720x.jpg)



![Начальное программирование на С++. Графики. Технические приложения. Часть 2. #include #include using namespace std; int main(){int i;int b=0;int a[8]={1,1,0,0,1,0,1,1};for (i=0; i](/img/tmb/11/1066648/d18b67a1bc59d9b44f4c40770c4d3904-720x.jpg)

















![Начальное программирование на С++. Графики. Технические приложения. Часть 2. #include #include using namespace std;double S=0;double R=0;int v[7]={60,70,80,90,100,110,120}; //массив скоростейdouble t[7]={0.7,0.65,0.55,0.4,1.2,1.,1.5}; /*массив](/img/tmb/11/1066648/262dcdf1bd05700096847180151b5d66-720x.jpg)