- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Нейронные сети
Содержание
- 2. 1. НейронНейронные сети и нейрокомпьютеры – это
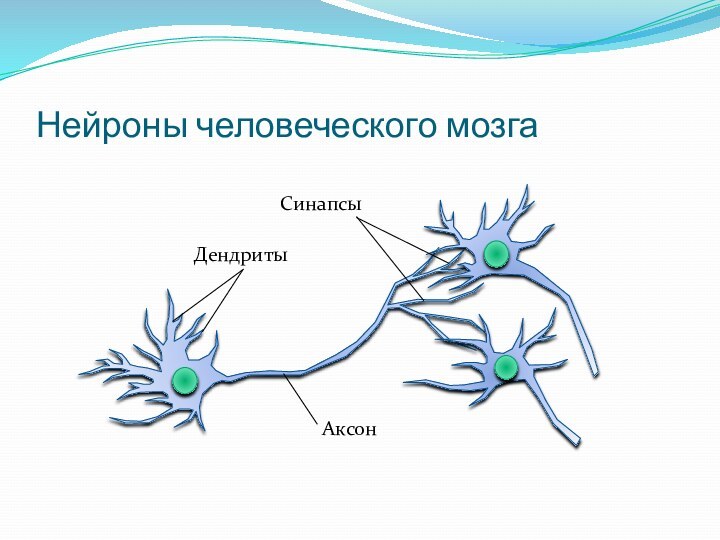
- 3. Нейроны человеческого мозгаАксонДендритыСинапсы
- 4. простейший нейрон может иметь до 10 000
- 5. 2. Математический нейрон Мак-Каллока – Питтса1943 г.
- 6. Активационная функцияа) функция единого скачка ( –
- 7. Математические нейроны, реализующие логические функцииматематический нейрон изображают
- 8. 3. Персептрон РозенблаттаИдея Мак-Каллока – Питтса была
- 10. Итерационный алгоритм корректировки весовых коэффициентов Шаг
- 11. 4. Многослойный персептронМ. Минский и С. Пайперт
- 12. Двухслойный персептрон, реализующий функцию "Исключающее ИЛИ" №
- 14. Алгоритм обратного распространения ошибкиШаг 1. Инициализация синаптических
- 15. на 5 шаге алгоритма вычисляется среднеквадратичная ошибка,
- 16. Задачи, решаемые с помощью нейросетейесли есть математическая
- 17. Невербальность и "шестое чувство" нейросетейКак и человеческий
- 18. Методы обучения нейросетей детерминистскиестохастическиеподстройка весов представляет собой
- 19. основная проблема обучения персептронов состоит в том,
- 20. Генетический алгоритмпредложен Дж. Холландом в 1970-х годахимитирует
- 21. Операция скрещивания, применяемая в генетических алгоритмах a1a2Хромосома отцаb1b2Хромосома материa1b2Хромосома 1-го потомкаb1a2Хромосома 2-го потомка
- 22. Подготовка входных параметровуспех создания нейронной сети во
- 23. Определение незначимых параметрованализа значений весовых коэффициентов входных
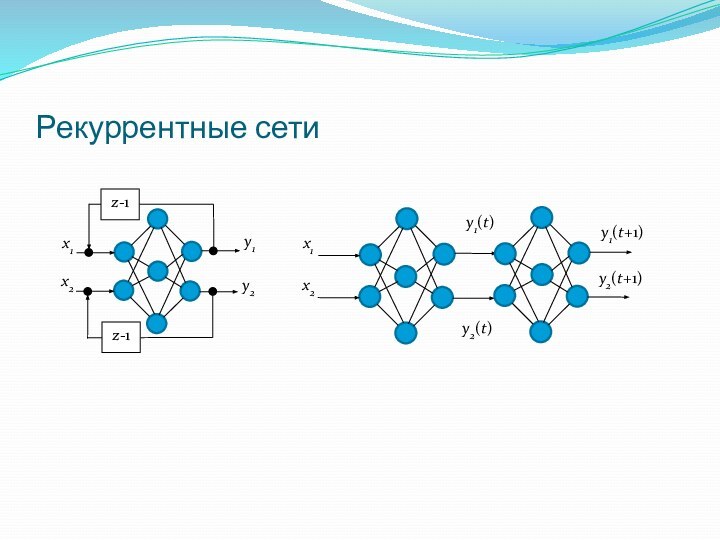
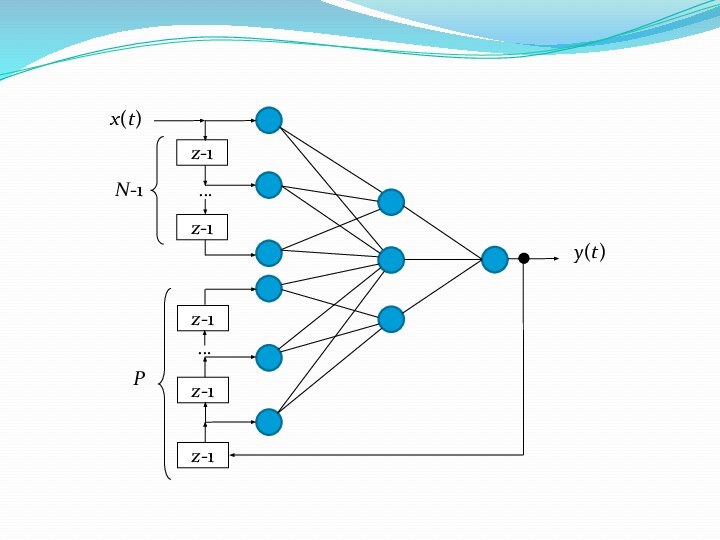
- 24. Рекуррентные сети
- 25. Скачать презентацию
- 26. Похожие презентации
1. НейронНейронные сети и нейрокомпьютеры – это одно из направлений компьютерной индустрии, в основе которого лежит идея создания искусственных интеллектуальных устройств по образу и подобию человеческого мозга.

















Слайд 4
простейший нейрон может иметь до 10 000 дендритов
человеческий
мозг содержит примерно 1011 нейронов
каждый нейрон связан с 103-104
другими нейронамимозг человека содержит 1014-1015 взаимосвязей
Слайд 5
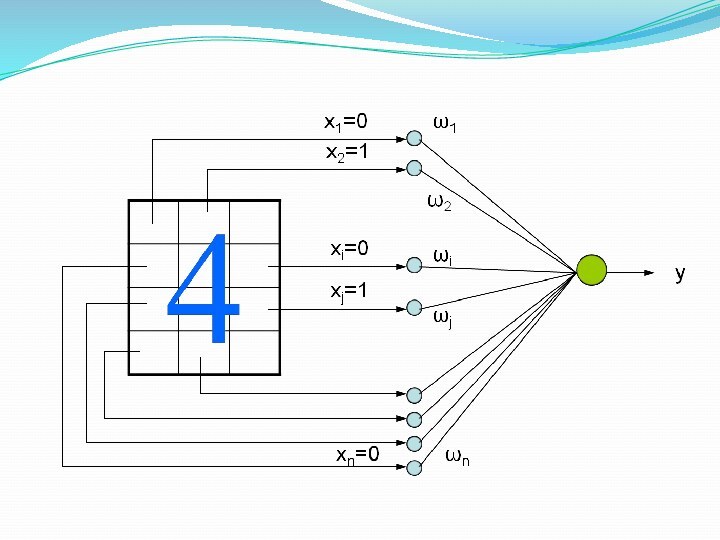
2. Математический нейрон Мак-Каллока – Питтса
1943 г. Уоррен
Мак-Каллок и Вальтер Питтс выдвинули гипотезу математического нейрона
математический нейрон
имеет несколько входов и один выходчерез входы (j) математический нейрон принимает входные сигналы (xj)
входные сигналы умножаются на весовой коэффициент (wj) и суммируются
выходной сигнал нейрона у является нелинейная функция f(S), которая называется активационной
Слайд 6
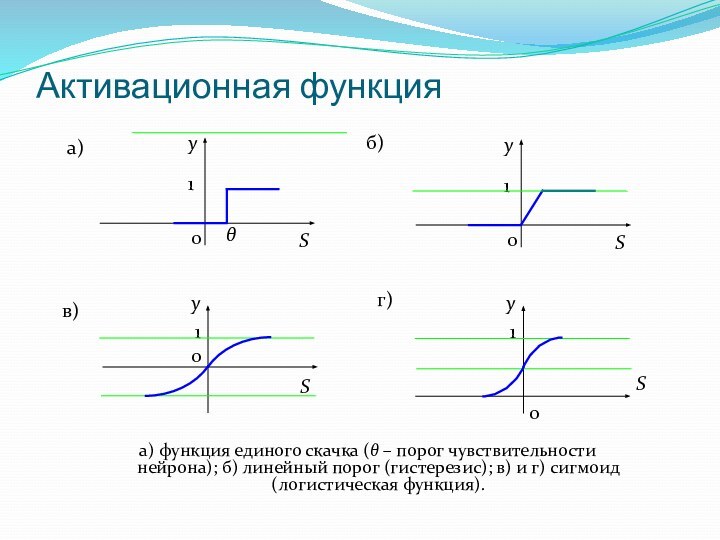
Активационная функция
а) функция единого скачка ( – порог
чувствительности нейрона); б) линейный порог (гистерезис); в) и г)
сигмоид (логистическая функция).
S
y
0
1
S
y
0
1
а)
б)
S
y
0
1
y
1
в)
г)
S
0
Слайд 7
Математические нейроны, реализующие логические функции
математический нейрон изображают кружочком
возбуждающий
вход – стрелкой
тормозящий вход – маленьким кружочком
рядом может записываться
число, показывающее значение порога x1
x2
y
= 2
"И"
x1
x2
y
= 1
"ИЛИ"
x
y
= 0
"НЕТ"
Слайд 8
3. Персептрон Розенблатта
Идея Мак-Каллока – Питтса была реализована
Фрэнком Розенблаттом:
1958 г. в виде компьютерной программы
1960 г. в
виде электронного устройства, моделирующего человеческий глаз
Слайд 10
Итерационный алгоритм корректировки
весовых коэффициентов
Шаг 1. Подать
входной образ и вычислить выход персептрона у
Шаг 2, а.
Если выход правильный, то перейти на шаг 1Шаг 2, б. Если выход неправильный и равен нулю, то увеличить веса активных входов, например:
wj(t + 1) = wj(t) + хj
Шаг 2, в. Если выход неправильный и равен единице, то уменьшить веса активных входов, например:
wj(t + 1) = wj(t) - хj
Шаг 3. Перейти на шаг 1 или завершить процесс обучения.
Слайд 11
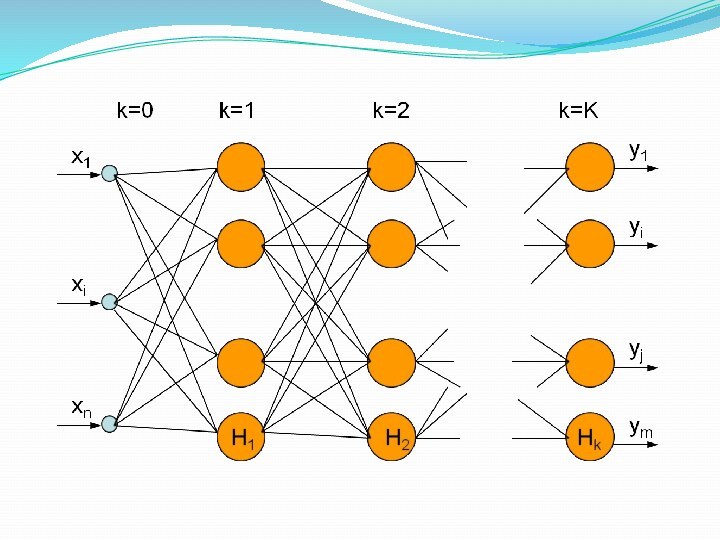
4. Многослойный персептрон
М. Минский и С. Пайперт в
своей книге "Персептроны" строго математически доказали, что однослойные персептроны
в принципе не способны решать многие простые задачиМногие понимали, что надо усложнять структуру персептронов
Слайд 12
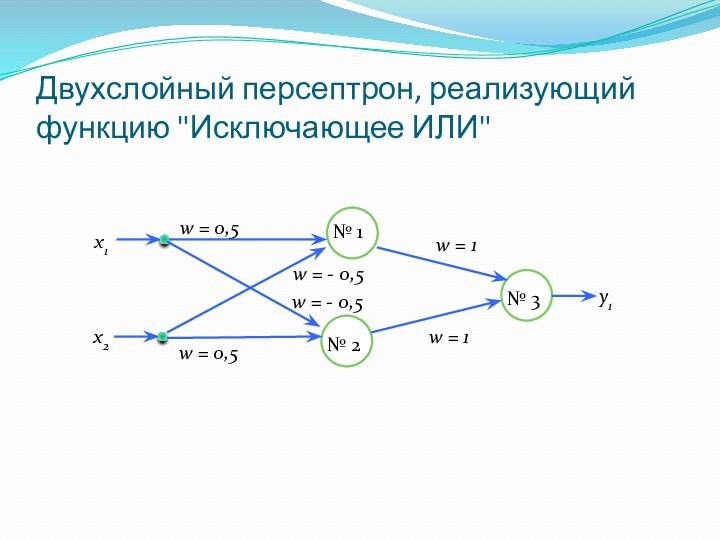
Двухслойный персептрон, реализующий функцию "Исключающее ИЛИ"
№ 1
№
Слайд 14
Алгоритм обратного распространения ошибки
Шаг 1. Инициализация синаптических весов
и смещений
Шаг 2. Представление из обучающей выборки входного вектора
Xq = (х1, х2, ..., xN)q и соответствующего ему выходного вектора Dq = (d1, d2, …, dM)qШаг 3. Прямой проход
Шаг 4. Обратный проход
Шаг 5. Повторение шагов 2–4 необходимое число раз
Слайд 15 на 5 шаге алгоритма вычисляется среднеквадратичная ошибка, усредненная
по всем обучающим примерам:
также вычисляется максимальная разность между желаемым
и фактическим выходами персептрона: итерационный процесс заканчивается после того, как погрешность , достигнет заданной величины, либо при достижении предельного числа эпох обучения.
Слайд 16
Задачи, решаемые с помощью нейросетей
если есть математическая модель
какого-то процесса, то изучая влияние входных параметров на выходные,
можно решить задачу оптимизации моделируемого процессаесли математическая модель является нестационарной, то её можно использовать для решения задач прогнозирования
если математическая модель работает в реальном режиме времени, то результаты математического моделирования могут быть оперативно переданы оператору, управляющему объектом, или могут быть непосредственно введены в приборы, что позволяет решать задачи управления моделируемым объектом или процессом
нейронные сети могут решать задачи распознавания и классификации образов, причем под образами понимаются зрительные изображения, символы, тексты, запахи, звуки, шумы
Слайд 17
Невербальность и "шестое чувство" нейросетей
Как и человеческий мозг,
нейросеть способна выводить закономерности, делать догадки, открывать законы природы.
Но, так же, как и человек, нейросеть не способна к чёткой формулировке алгоритма, позволившего сделать то или иное умозаключение.Известны случаи, когда нейросети демонстрируют феномен, называемый в жизни шестым чувством. Они с успехом извлекают знания из анализа информации, из которой, казалось бы, эти знания извлечь невозможно.
Слайд 18
Методы обучения нейросетей
детерминистские
стохастические
подстройка весов представляет собой жёсткую
последовательность действий
подстройка весов производится на основе действий, подчиняющихся некоторому
случайному процессуСлайд 19 основная проблема обучения персептронов состоит в том, что
поверхность функции ошибок обычно имеет очень сложную форму со
множеством локальных минимумов.актуальным является развитие методов глобальной оптимизации, которые позволяют найти глобальный минимум многоэкстремальной целевой функции
Слайд 20
Генетический алгоритм
предложен Дж. Холландом в 1970-х годах
имитирует природный
оптимизационный процесс, происходящий при эволюции живых организмов
основные идеи теории
Чарльза Дарвина: естественный отбор и генетическое наследованиемутация – изменение генов
Слайд 21
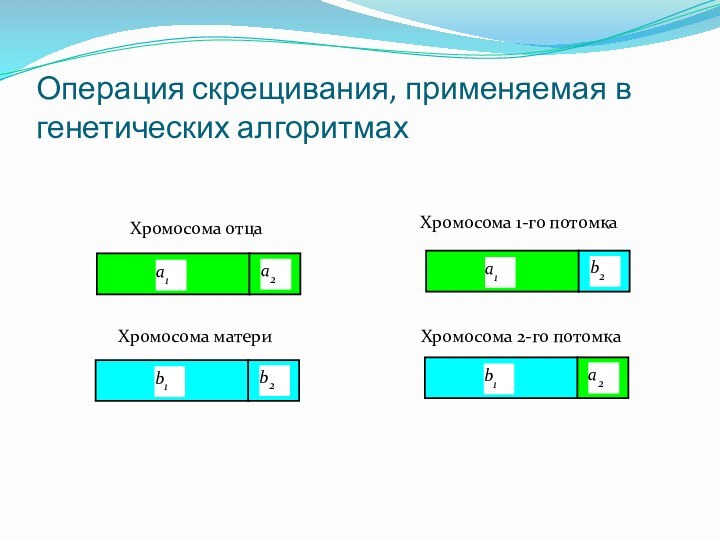
Операция скрещивания, применяемая в генетических алгоритмах
a1
a2
Хромосома отца
b1
b2
Хромосома
матери
a1
b2
Хромосома 1-го потомка
b1
a2
Хромосома 2-го потомка
Слайд 22
Подготовка входных параметров
успех создания нейронной сети во многом
зависит от удачного подбора обучающих примеров
следует учитывать, что
не все параметры предметной области влияют на выходной вектор Yнезначимые параметры не следует включать в список параметров входного вектора X
на первом этапе в вектор X включают как можно больше параметров
Слайд 23
Определение незначимых параметров
анализа значений весовых коэффициентов входных нейронов.
Если у какого-либо входного нейрона синаптические веса значительно меньше,
чем у других нейронов, то этот входной нейрон скорее всего соответствует незначимому параметру вектора Xвозмущения значений входных параметров и анализа реакции сети на эти возмущения. Если сеть не реагирует или слабо реагирует на изменения значения какого-либо входного параметра, то этот параметр не является значимым