Слайд 2
Цифровая интегральная схема (ИС) – это микроэлектронное изделие,
изготовленное методами интегральной технологии (чаще полупроводниковой), заключенное в самостоятельный
корпус и выполняющее определенную функцию преобразования дискретных (цифровых) сигналов.
Простейшие преобразования над цифровыми сигналами осуществляют цифровые ИС, получившие названия логических элементов (ЛЭ).
Логические элементы относятся к элементам дискретного действия, характеризующихся двумя устойчивыми состояниями. Переход от одного состояния в другое происходит скачком. Сигналы на выходе логического элемента имеют место лишь при определенном сочетании сигналов на входе.
Слайд 3
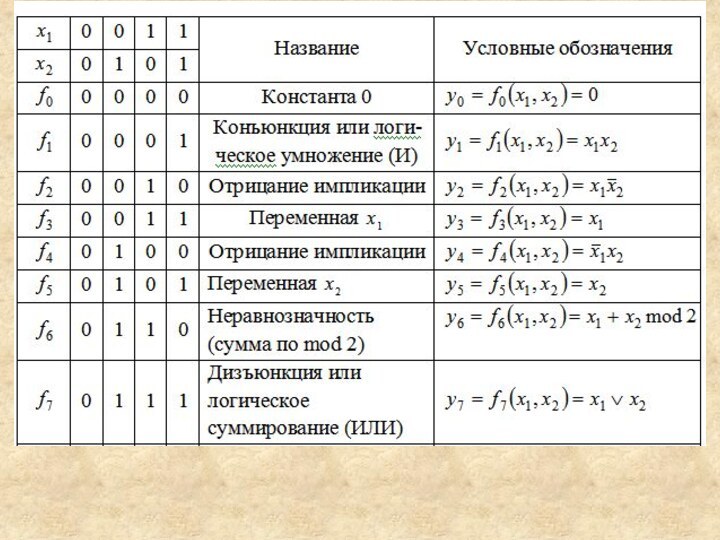
Зависимость выходного сигнала от сочетания входных называется логической
функцией.
Для математического описания логических функций и операций существует специальная
алгебра логики (алгебра Буля) Алгебра логики – это формальный аппарат описания логической стороны процессов в цифровых устройствах.
Слайд 4
Различным соединением простейших ЛЭ друг с другом можно
выполнять логическую функцию любой сложности.
Общие условные обозначения простейших
логических элементов
Слайд 5
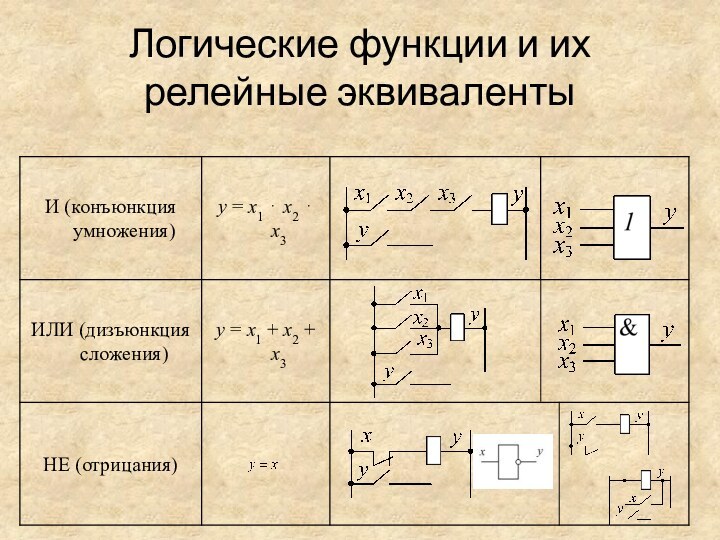
Логические функции и их релейные эквиваленты
Слайд 6
Набор трех логических функций: НЕ, И, ИЛИ называют
булевым базисом:
И – конъюнкция, логическое умножение, в релейно-контактной технике
реализуется последовательным включением замыкающих контактов, управляемых сигналами аргументами. Может использоваться как вентиль.
НЕ – инвертор, в релейно-контактной системе реализуется как размыкающий контакт.
ИЛИ – дизъюнкция, логическое сложение, реализуется параллельным включением контактов.
Слайд 7
С помощью набора функций НЕ, И, ИЛИ можно
выразить любую логическую функцию, сколь сложной бы она ни
была.
Функция И – НЕ – это функция двух и более аргументов, другими словами функция Шеффера.
Любой сигнал 0 на входе дает на выходе 1 и наоборот – все единицы на выходе дают 0 на выходе, т.е.
Слайд 8
Эта функция обладает логической полнотой и с помощью
одной лишь функции И – НЕ можно построить любую
сколь угодно сложную функцию. Вторым цепным ее свойством является то, что именно ее удалось эффективно реализовать средствами самой массовой интегральной технологии – ТТЛ. Поэтому уже четверть века функция И – НЕ наиболее распространена в цифровой автоматике.
Слайд 9
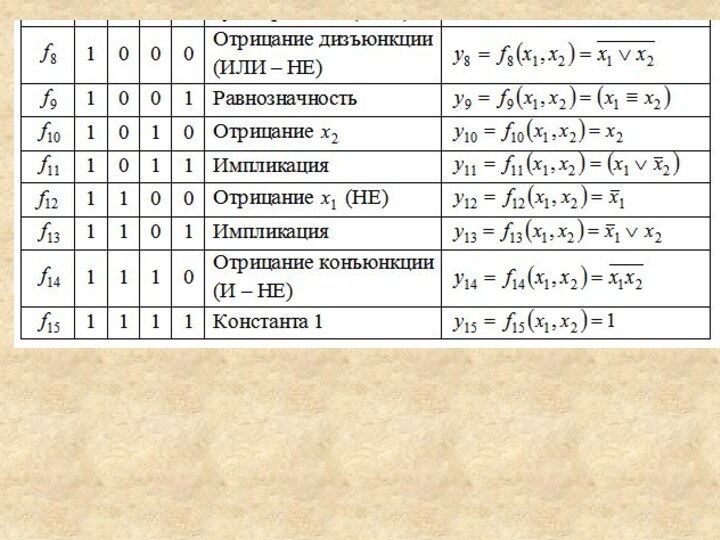
Функция ИЛИ – НЕ – функция Вебба.
Эта функция также обладает логической полнотой и тоже удобна
для интегрального исполнения, а особенно по технологии КМДП комплементарные металл диэлектрик п\проводник и ЭСЛ Эмиттерно-связанная логика.
Слайд 12
Основные тождественные отношения булевой алгебры
Слайд 14
Для этого введены следующие обозначения:
Обозначение двух
видов входной переменной х.
Переменную х без отрицания обозначим х^1,
Переменную
х с отрицанием обозначим х^0,
Слайд 15
Дизъюнкцию от n аргументов хi обозначим
т.е
Набор аргументов хi, т.е. выражение составного кодового
сигнала, обозначим
Тогда
Слайд 16
Для любой функции и для любого i возможно
соотношение
которое легко проверить, подставляя в левую и правую части
значения xi = 0 и xi = 1. Применяя соотношение (6.1) последовательно к переменной x1,x2,…,xn, получим
, а
дизьюнкция берется по всем параметрам
Представление функции по этой форме называется совершенной дизъюнктивной нормальной формой (СДНФ) функции.
Слайд 18
Рассмотрим пример. Для функции
СДНФ имеет вид
Поскольку для функции f6 выполняются условия
то
Слайд 19
Комбинационная схема, построенная по СНФ, как правило, может
быть упрощена.
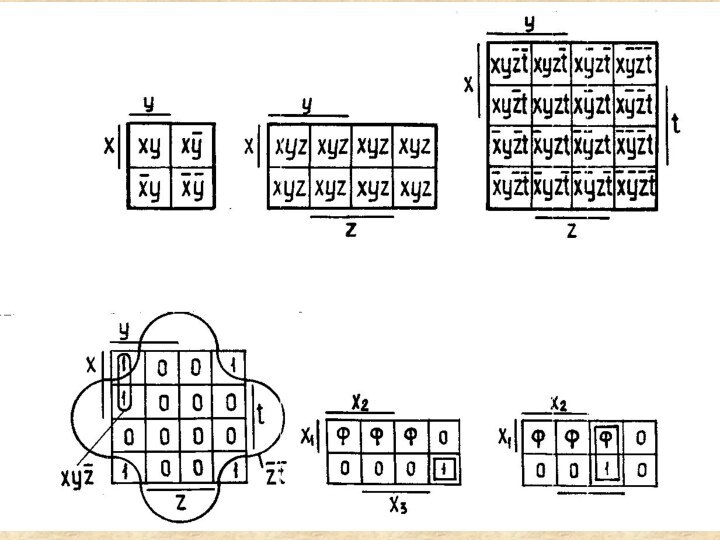
Упрощение (минимизация) СНФ функции удобно производить при
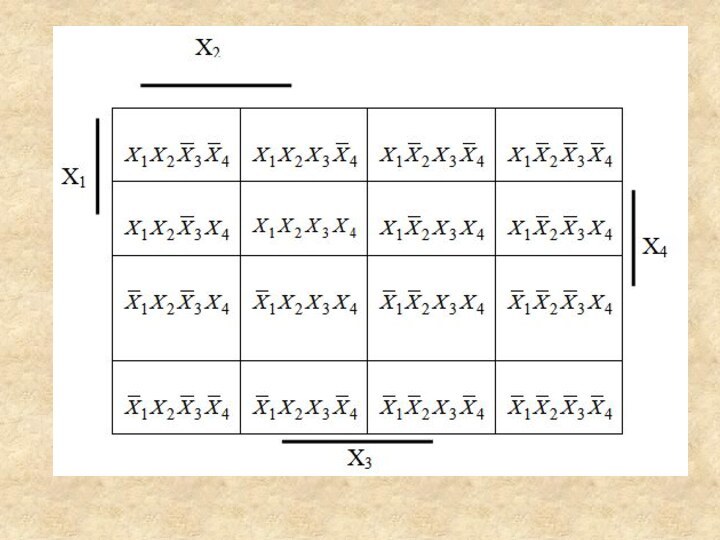
помощи таблиц, в которых все соседние конъюнкции находятся рядом. Такая таблица называется диаграммой Вейча. Для функций, зависящих от двух, трех, четырех переменных, диаграммы Вейча показаны на рисунке
Слайд 21
Рассмотрим пример. Пусть задана функция
Наличие 1 в данной
клетке диаграммы Вейча означает, что в СДНФ функции имеется
конъюнкция, указанная в данной клетке, а наличие 0 означает отсутствие указанной конъюнкции в СДНФ упрощаемой функции. Из диаграммы Вейча (рисунок 6.2) видно, что эта функция содержит две группы соседних конъюнкций. Одна группа состоит из двух конъюнкций , а вторая из четырех – .
Слайд 22
После склеивания по указанным группам получим упрощенное представление
функции
Таким образом, нахождение по диаграмме Вейча минимальный ДНФ сводится
к отысканию наиболее коротких конъюнкций, покрывающих все единицы функции.