- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Подходы к измерению информации
Содержание
- 2. СодержаниеКоличество информации как мера уменьшения неопределенности знанийОпределение количества информацииАлфавитный подход к определению количества информации
- 3. Количество информации как мера уменьшения неопределенности знаний
- 4. СообщениеЛюди обмениваются информацией в форме сообщений.Сообщение –
- 5. Информативность сообщенияДля разных людей одно и то
- 6. ПримерыВопрос:- Содержит ли информацию вузовский учебник по
- 7. ПримерыВопрос: - Какой город является столицей Франции?Ответ:-
- 8. ПримерыВопрос:- Что изучает коллоидная химия?Ответ:- Коллоидная химия
- 9. ПримерыВопрос:- Какую высоту и вес имеет Эйфелева
- 10. Информативность сообщенияЕсли сообщение неинформативно для человека, то
- 11. Информация и неопределенностьДопустим, вы оказались на перекрестке
- 12. Информация и неопределенностьПример: вы услышали по телевизору,
- 13. Информация и неопределенностьПодобное происходит всякий раз, когда
- 14. Информация и неопределенностьЭту интуитивно ясную связь между
- 15. Неопределенность знанийНеопределенность знаний - сообщение, которое содержит
- 16. Информация и неопределенностьТаким образом, если мы хотим
- 17. Информация и неопределенностьСделаем это на моделях простейших систем.Пусть в нашем распоряжении имеются монета и игральный кубик.
- 18. Бросание монетУ монеты, как известно, две стороны:«герб»
- 19. Бросание кубикаИгральный кубик — это кубик, грани
- 20. Неопределенность знанийНеопределенность знания о результате некоторого события
- 21. Случайность выбораЕсть еще одна особенность возникновения информации
- 22. Равновероятные событияСобытия равновероятны, если ни одно из
- 23. Неравновероятностные событияНеравновероятные события: в сообщении о погоде
- 24. Симметричные событияВыбор состояния после подбрасывания монеты или
- 25. Симметричные события не всегда симметричны!«Однажды в детстве
- 26. Задания для закрепленияОпределите, какое из сообщений является
- 27. Задания для закрепленияДайте следующим сообщениям оценки «важная»,
- 28. Задания для закрепленияВероятность какого события больше:В коробке
- 29. Определение количества информации
- 30. Как же измерить количество информации?Да также, как
- 31. Достоверное и невозможные событияДостоверное событие - событие,
- 32. 1 бит информацииСообщение, уменьшающее неопределенность знаний в
- 33. Определение информацииЕсли «Ваньку-Встаньку» качнуть, то сколько различных
- 34. Определение информацииБудем бросать монету.Сколько вариантов выпадения может
- 35. Определение информацииБудем бросать 2 монеты.Бросание 2 монет
- 36. Определение информацииБудем бросать 3 монеты.При бросание 3
- 37. Отгадывание чиселДопустим кто-то загадал число от 1
- 38. Стратегия отгадывания чиселКак оптимально отгадывать загаданное число?Правильная
- 39. Сценарий отгадывания числаПусть загадано число 5 (мы
- 40. Определение информацииА если мы будем бросать 6-гранный
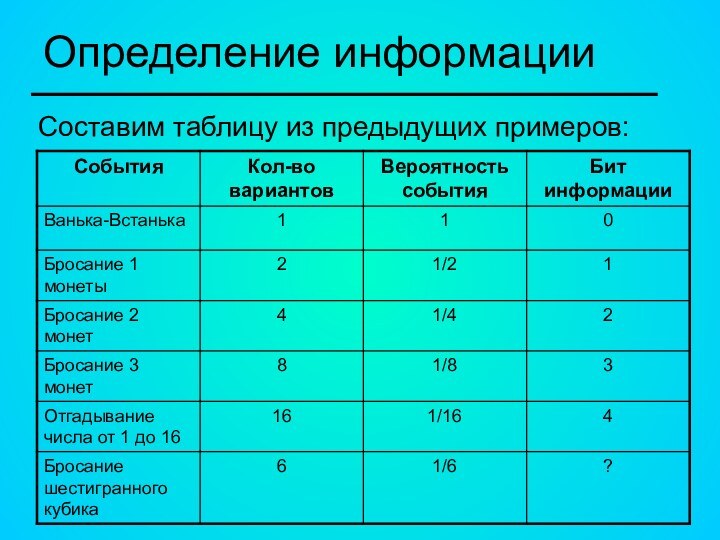
- 41. Определение информацииСоставим таблицу из предыдущих примеров:
- 42. Определение информацииЕсли посмотреть таблицу, то можно заметить
- 43. Определение информацииЕсли N = 2 (2=21),то уравнение
- 44. Определение информацииДля тех значений N, которые не
- 45. Задания для закрепленияПример 1.Сколько информации несет сообщение
- 46. Задания для закрепленияПример 2.Сколько информации несет сообщение
- 47. Задания для закрепленияПример 3.Проводятся две лотереи «4
- 48. 1 вариант решения:Вытаскивание любого номера из лотерейного
- 49. Выбор первого шара производится из 32-х шаров
- 50. Задания для закрепленияПример 4.В течение четверти ученик
- 51. Самостоятельное решениеЗадача 1.Вы подошли к светофору, когда
- 52. Самостоятельное решениеЗадача 2.Вы подошли к светофору, когда
- 53. Самостоятельное решениеЗадача 3.В корзине 8 шаров.Все шары
- 54. Самостоятельное решениеЗадача 4.Сколько бит информации несет сообщение
- 55. Самостоятельное решениеЗадача 5.в школьной библиотеке 16 стеллажей
- 56. Самостоятельное решениеЗадача 6.При угадывании целого числа в
- 57. Самостоятельное решениеЗадача 7.Сообщение о том, что Петя
- 58. ОтветыЗадача 1. 1 бит.Задача 2. 0 бит.Задача
- 59. Алфавитный подход к определению количества информации
- 60. Существует и другой способ измерения количества информации
- 61. Алфавитный подход удобен при подсчете количества информации,
- 62. АлфавитАлфавит – конечное множество символов, используемых для представления информации.
- 63. Мощность алфавитаЧисло символов в алфавите называется мощностью
- 64. Количество информации, которое несет в тексте каждый
- 65. Какова минимальная мощность алфавита, с помощью которого можно записывать (кодировать информацию)?
- 66. Односимвольный алфавитСообщение любой длины, использующее односимвольный алфавит,
- 67. ПримерПредставьте себе толстую книгу в 1000 страниц,
- 68. Минимальная мощность алфавитаМинимальная мощность алфавита, пригодного для
- 69. Мощность русского алфавитаКаждая буква русского алфавита (если
- 70. Компьютерный алфавитСовременный компьютер может обрабатывать числовую, текстовую,
- 71. БайтКомпьютер для внешнего представления текстов и другой
- 72. Производные единицы измерения информацииКилобайт больше байта в
- 73. Задачи для закрепленияЗадача 1.Книга, набранная с помощью
- 74. Задачи для закрепленияЗадача 2.Объем сообщения, содержащего 2048
- 75. Задачи для самостоятельного решенияЗадача 1.Алфавит племени Мульти
- 76. Задачи для самостоятельного решенияЗадача 3.Племя Мульти имеет
- 77. Задачи для самостоятельного решенияЗадача 4.Информационное сообщение объемом
- 78. Задачи для самостоятельного решенияЗадача 6.Сколько килобайтов составит
- 79. Задачи для самостоятельного решенияЗадача 8.Сообщение занимает 3
- 80. Задачи для самостоятельного решенияЗадача 9.Для записи сообщения
- 81. Скачать презентацию
- 82. Похожие презентации
















































































Слайд 2
Содержание
Количество информации как мера уменьшения неопределенности знаний
Определение количества
информации
Слайд 4
Сообщение
Люди обмениваются информацией в форме сообщений.
Сообщение – это
и речь, которую мы слушаем (радиосообщение, объяснение учителя), и
воспринимаемые нами зрительные образы (фильм по телевизору, сигнал светофора), и текст книги, которую мы читаем и т. д.Информативным назовем сообщение, которое пополняет знания человека, то есть несет для него информацию.
Слайд 5
Информативность сообщения
Для разных людей одно и то же
сообщение с точки его информативности может быть разным.
Если сведения
«старые», то есть человек это уже знает, или содержание сообщения непонятно человеку, то для него это сообщение неинформативно.Информативно то сообщение, которое содержит новые и понятные сведения.
Слайд 6
Примеры
Вопрос:
- Содержит ли информацию вузовский учебник по высшей
математике с точки зрения первоклассника?
Ответ:
- Да, содержит с любой
точки зрения!Потому что в учебнике заключены знания людей: авторов учебника, создателей математического аппарата (Ньютона, Лейбница и др.), современных математиков.
Другой вопрос:
- Будет ли информативным текст этого учебника для первоклассника, если он попытается его прочитать?
Иначе говоря, может ли первоклассник с помощью этого учебника пополнить собственные знания?
Очевидно, что ответ отрицательный.
Читая учебник, то есть, получая сообщения, первоклассник ничего не поймет, а, стало быть, не обратит его в собственные знания.
Слайд 7
Примеры
Вопрос:
- Какой город является столицей Франции?
Ответ:
- Столица
Франции – Париж.
Сообщение информативно?
- Нет, так как известно.
Слайд 8
Примеры
Вопрос:
- Что изучает коллоидная химия?
Ответ:
- Коллоидная химия изучает
дисперсионные состояния систем, обладающих высокой степенью раздробленности.
Сообщение информативно?
- Нет,
так не понятно.
Слайд 9
Примеры
Вопрос:
- Какую высоту и вес имеет Эйфелева башня?
Ответ:
- Эйфелева башня имеет
высоту 300 метров
и вес 9000 тонн.
Сообщение
информативно:- Да.
Слайд 10
Информативность сообщения
Если сообщение неинформативно для человека, то количество
информации в нем с точки зрения этого человека равно
нулю.Количество информации в информативном сообщении больше нуля.
Слайд 11
Информация и неопределенность
Допустим, вы оказались на перекрестке в
незнакомом городе и не знаете, как пройти к вокзалу.
Ваше
состояние можно охарактеризовать, как состояние неопределенности.Но вот прохожий объяснил дорогу к вокзалу.
Теперь у вас появилась информация, а неопределенность пропала.
Слайд 12
Информация и неопределенность
Пример: вы услышали по телевизору, что
завтра будет солнечная погода.
Ваше состояние изменилось: вы стали обладателем
информации, а неопределенность, которая до этого существовала, исчезла.
Слайд 13
Информация и неопределенность
Подобное происходит всякий раз, когда у
вас появляется та или иная информация, — неопределенность, если
она до этого имела место, уменьшается или вовсе ликвидируется.
Слайд 14
Информация и неопределенность
Эту интуитивно ясную связь между обыденными
представлениями об информации и о неопределенности можно сформулировать так:
Появление
информации суть уменьшение неопределенности.
Слайд 15
Неопределенность знаний
Неопределенность знаний - сообщение, которое содержит сведения
о том, что произошло одно из конечного множества (N)
возможных событий.
Слайд 16
Информация и неопределенность
Таким образом, если мы хотим получить
более отчетливое представление об информации, стоит поразмышлять о том,
что же такое неопределенность и можно ли каким-то образом оценить ее количественно.
Слайд 17
Информация и неопределенность
Сделаем это на моделях простейших систем.
Пусть
в нашем распоряжении имеются монета и игральный кубик.
Слайд 18
Бросание монет
У монеты, как известно, две стороны:
«герб» «решка»
Если бросить ее на стол, монета обязательно упадет вверх
либо «гербом», либо «решкой».Таким образом, монету, лежащую на столе, можно рассматривать как простейшую систему, которая может находиться в одном из двух возможных состояний.
Слайд 19
Бросание кубика
Игральный кубик — это кубик, грани которого
пронумерованы от 1 до 6.
Аналогично монете игральный кубик, лежащий
на столе, — это система, находящаяся в одном из шести возможных состояний (по номерам граней, обращенных вверх).
Слайд 20
Неопределенность знаний
Неопределенность знания о результате некоторого события –
это число возможных вариантов результата.
Для монеты – 2, для
кубика – 6, для билетов – 30 (если на столе лежало 30 билетов).Чем больше равновозможных событий, тем больше неопределенность ситуации.
Выбор одного из возможных состояний ликвидирует неопределенность, создавая тем самым информацию.
Слайд 21
Случайность выбора
Есть еще одна особенность возникновения информации –
случайность выбора, которая в полной мере демонстрируется на наших
примерах.Ну а если бы Вы, стоя на перекрестке, так и не дождались ни одного прохожего, Вам ничего не оставалось бы делать, как положиться на счастливый случай и выбрать дорогу наугад.
Тогда характер Вашего поведения при наличии двух возможных направлений движения в точности совпал бы с характером поведения монеты.
Слайд 22
Равновероятные события
События равновероятны, если ни одно из них
не имеет преимущества перед другими.
С этой точки зрения выпадение
«герба» или «решки» – равновероятно.
Слайд 23
Неравновероятностные события
Неравновероятные события: в сообщении о погоде в
зависимости от сезона сведения о том, что будет дождь
или снег, могут иметь разную вероятность.Летом наиболее вероятно сообщение о дожде, зимой – о снеге, а в переходный период (в марте или ноябре) они могут оказаться равновероятными.
Слайд 24
Симметричные события
Выбор состояния после подбрасывания монеты или кубика
происходит симметрично.
Это значит, что отсутствуют какие-либо факторы, способные обусловить
преимущественное попадание системы в то или иное состояние: выбор происходит случайно, причем все состояния равно возможны.Проверить, так ли это на самом деле, можно, проделав большое число бросаний, регистрируя каждый раз состояние, в котором оказалась монета.
По мере роста количества бросаний доли «гербов» и «решек» в общем числе бросаний будут все меньше и меньше отличатся друг от друга.
Слайд 25
Симметричные события не всегда симметричны!
«Однажды в детстве я
уронил бутерброд. Глядя, как я виновато вытираю масляное пятно,
оставшееся на полу, старший брат успокоил меня:- Не горюй, это сработал закон бутерброда.
- Что еще за закон такой? - спросил я.
- Закон, который гласит: "Бутерброд всегда падает маслом вниз". Впрочем, это шутка, - продолжал брат.- Никакого закона нет. Просто бутерброд действительно ведет себя довольно странно: большей частью масло оказывается внизу.
- Давай-ка еще пару раз уроним бутерброд, проверим, - предложил я. - Все равно ведь его придется выкидывать.
Проверили. Из десяти раз восемь бутерброд упал маслом вниз.
И тут я задумался: а можно ли заранее узнать, как сейчас упадет бутерброд маслом вниз или вверх?
Наши опыты прервала мать…" ( Отрывок из книги "Секрет великих полководцев", В.Абчук).
Слайд 26
Задания для закрепления
Определите, какое из сообщений является для
Вас информативным:
Площадь Тихого океана – 179 млн. кв. км.
Москва
– столица России.Вчера весь день шел дождь.
Завтра ожидается солнечная погода.
Дивергенция однородного векторного поля равна нулю.
Dog – собака (по-английски).
Ro do, may si, lot do may.
2*2 = 4.
Содержание
Слайд 27
Задания для закрепления
Дайте следующим сообщениям оценки «важная», «полезная»,
«безразличная», «вредная» информации:
Сейчас идет дождь.
Занятия факультатива по информатике проводятся
каждый вторник.IBM – это первые буквы английских слов, которые звучат как «интернешнел бизнес машина», что по-русски означает «машины для международного бизнеса».
Завтра будет контрольная работа по физике.
Чтобы родители не узнали про двойку, надо вырвать страницу из дневника.
Лед – это твердое состояние воды.
Первым человеком, полетевшим в космос, был Юрий Гагарин.
Номер телефона скорой помощи 02
Содержание
Слайд 28
Задания для закрепления
Вероятность какого события больше:
В коробке имеется
50 шаров. Из них 40 белых и 10 черных. Вероятность вытащить
белый или черный шар.Сереже – лучший ученик в классе. Вероятность получения за контрольную по математике 5 или 2.
В пруду живут 8000 карасей, 2000 щук и 400000 пескарей. Вероятнее наловить больше карасей, щук или пескарей.
Содержание
Слайд 30
Как же измерить количество информации?
Да также, как мы
измеряем длину или массу чего-нибудь: сравнить с соответствующим эталоном.
Надо
только выбрать эталон.Например, в мультфильме
«38 попугаев» эталоном длины
служит длина шага попугая.
Каков же эталон для измерения информации?
Давайте в этом разберемся.
Слайд 31
Достоверное и невозможные события
Достоверное событие - событие, которое
обязательно происходит
Невозможное событие – никогда не произойдет.
Вероятность достоверного события
равна 1, а невозможного – 0.Это крайние значения, то есть во всех других «промежуточных» случаях значение вероятности лежит между нулем и единицей.
Вероятность каждого из двух равновероятных событий равна ½.
Слайд 32
1 бит информации
Сообщение, уменьшающее неопределенность знаний в 2
раза, несет 1 бит информации.
Сообщение о том, что
произошло одно событие из двух равновероятных, несет 1 бит информации.Бит - binary digit (двоичный знак).
Слайд 33
Определение информации
Если «Ваньку-Встаньку» качнуть, то сколько различных вариантов
его конечного состояния получим?
- Один вариант («Ванька-Встанька» всегда встает).
То
есть вероятность события равна 1 (100% выполнение).И мы не получаем ни чего нового и неизвестного при этом, то есть информация равна 0.
Слайд 34
Определение информации
Будем бросать монету.
Сколько вариантов выпадения может быть?
– 2
Вероятность выпадения «герба» или «решки» - ½.
Количество информации
– 1 бит.
Слайд 35
Определение информации
Будем бросать 2 монеты.
Бросание 2 монет должно
принести 2 бита информации, так количество монет увеличилось в
2 раза.Количество различных вариантов выпадения по две монеты: 4.
Вероятность появления 1 варианта – ¼
Слайд 36
Определение информации
Будем бросать 3 монеты.
При бросание 3 монет
количество информации увеличится в 3 раза по сравнению с
бросанием 1 монеты.Количество различных вариантов выпадения по 3 монеты: 8
Вероятность выпадения 1 варианта: 1/8.
Слайд 37
Отгадывание чисел
Допустим кто-то загадал число от 1 до
16.
Сколько чисел можно загадать? - 16.
Вероятность загадать любого числа
из этого промежутка: 1/16.Отгадывание происходит по такому сценарию:
Задается такой вопрос на который можно получить один из вариантов ответа: «да» или «нет».
Слайд 38
Стратегия отгадывания чисел
Как оптимально отгадывать загаданное число?
Правильная стратегия
состоит в том, что вопросы нужно задавать так, чтобы
количество возможных вариантов каждый раз уменьшалось вдвое.Тогда количество возможных событий в каждом из полученных подмножеств будет одинаково, и их отгадывание - равновероятно.
Слайд 39
Сценарий отгадывания числа
Пусть загадано число 5 (мы не
знаем это).
1 вопрос (даст 1 бит информации):
- Больше 8?
– Нет.2 вопрос (даст 2 бит информации):
- Больше 4? – Да.
3 вопрос (даст 3 бит информации):
-Больше 6? – Нет.
4 вопрос (даст 4 бит информации):
-Больше 5? – Нет.
Ответ: Задуманное число 5.
Вывод:
При отгадывании задуманного числа в диапазоне от 1 до 16, достаточно 4 вопроса (получение 4 бита информации).
Слайд 40
Определение информации
А если мы будем бросать 6-гранный кубик?
Количество
вариантов выпадения одной из 6 сторон: 6.
Вероятность выпадения одной
из 6 сторон: 1/6.Сколько же будет получено
информации при выпадении
одной из 6 сторон?
Слайд 42
Определение информации
Если посмотреть таблицу, то можно заметить закономерность.
От
частных примеров приходим к обобщенной формуле:
Если ввести обозначения:
N –
число вариантов равновероятных событий (неопределенность знаний),i – количество информации в сообщении о том, что произошло одно из N событий.
N = 2i
Если N известно, а i является неизвестной величиной, то данная формула превращается в показательное уравнение, которое решается с помощью функции логарифма:
i = log2N.
Слайд 43
Определение информации
Если N = 2 (2=21),
то уравнение примет
вид 2i = 21,
отсюда i = 1.
Если N =
4 (4=22),то уравнение примет вид 2i = 22,
отсюда i = 2.
Если N = 8 (8=23),
то уравнение примет вид 2i = 23,
отсюда i = 3.
В общем случае, если N = 2k,
где k- целое число,
то уравнение примет вид 2i = 2k,
отсюда i = k.
Слайд 44
Определение информации
Для тех значений N, которые не являются
целыми степенями двойки, решение уравнения можно получить из приведенной
в учебнике таблицы.Например, желая определить, сколько же бит информации несет сообщение о результате бросания шестигранного кубика, нужно решить уравнение
2i = 6.
Поскольку 22 < 6 < 23, то получаем 2 < i < 3.
Заглянув в таблицу, узнаем, что i=2,58496.
Слайд 45
Задания для закрепления
Пример 1.
Сколько информации несет сообщение о
том, что из колоды карт достали карту красной масти?
Решение:
1
бит, т. к. красных и черных карт одинаковое количество.Содержание
Слайд 46
Задания для закрепления
Пример 2.
Сколько информации несет сообщение о
том, что из колоды карт достали карту бубновой масти?
Решение:
2
бита, так как всего в колоде 4 масти, и количество карт в них одинаковое.Содержание
Слайд 47
Задания для закрепления
Пример 3.
Проводятся две лотереи «4 из
32» и «5 из 64».
Сообщение о результатах, какой из
лотерейнесет больше информации?
Содержание
Слайд 48
1 вариант решения:
Вытаскивание любого номера из лотерейного барабана
– события равновероятные.
Поэтому в первой лотерее количество информации в
сообщении об одном номере равно 5 бит (25 = 32), а во втором – 6 бит (26 = 64).Сообщение о 4-х номерах в первой лотерее несет 5 * 4 = 20 бит.
Сообщение о 5-ти номерах второй лотереи несет 6 * 5 = 30 бит.
Следовательно, сообщение о результатах второй лотереи несет больше информации, чем первой.
Содержание
Слайд 49 Выбор первого шара производится из 32-х шаров в
барабане.
Результат несет 5 бит информации.
Но 2-й шар будет выбираться
уже из 31 номера, 3-й – из 30 номеров, 4-й – из 29 номеров.Значит, количество информации, которое несет 2-й номер, находится из уравнения 2i = 31 (i = 5,95420 бит).
Для 3-го номера 2i = 30 (i = 4,90689 бит).
Для 4-го номера 2i =29 (i = 4,85798 бит).
В сумме получаем:
5 + 4,95420 + 4,90689 + 4,85798 = 19, 71907
Аналогично и для второй лотереи.
Окончательный вывод получается тот же, но результат вычислений более точен.
Содержание
2 вариант решения:
Слайд 50
Задания для закрепления
Пример 4.
В течение четверти ученик получил
100 оценок.
Сообщение о том, что он получил четверку, несет
2 бита информации.Сколько четверок ученик получил за четверть?
Решение:
Данный результат мог быть получен путем следующих рассуждений:
2 бита информации несет сообщение об одном из четырех равновероятных событий (22 = 4).
То есть вероятность получения четверок равна ¼.
Тогда количество четверок определится как:
100 / 4 = 25.
Таким образом, в течение четверти ученик получил 25 четверок.
Содержание
Слайд 51
Самостоятельное решение
Задача 1.
Вы подошли к светофору, когда горел
желтый свет.
После этого загорелся зеленый.
Какое количество информации вы при
этом получили?Содержание
Слайд 52
Самостоятельное решение
Задача 2.
Вы подошли к светофору, когда грел
красный свет.
После этого загорелся желтый свет.
Сколько информации вы при
этом получили?Содержание
Слайд 53
Самостоятельное решение
Задача 3.
В корзине 8 шаров.
Все шары разного
цвета.
Сколько информации несет сообщение о том, что из корзины
достали красный шар?Содержание
Слайд 54
Самостоятельное решение
Задача 4.
Сколько бит информации несет сообщение о
том, что из колоды в 32 карты достали даму
крести?Содержание
Слайд 55
Самостоятельное решение
Задача 5.
в школьной библиотеке 16 стеллажей с
книгами.
На каждом стеллаже 8 полок.
Библиотекарь сообщил Пете, что нужная
ему книга находится на пятом стеллаже на третьей сверху полке.Какое количество информации библиотекарь передал Пете?
Содержание
Слайд 56
Самостоятельное решение
Задача 6.
При угадывании целого числа в некотором
диапазоне было получено 6 бит информации.
Сколько чисел содержится в
этом диапазоне?Содержание
Слайд 57
Самостоятельное решение
Задача 7.
Сообщение о том, что Петя живет
во втором подъезде, несет 3 бита информации.
Сколько подъездов в
доме?Содержание
Слайд 58
Ответы
Задача 1. 1 бит.
Задача 2. 0 бит.
Задача 3.
3 бита.
Задача 4. 5 бит.
Задача 5. 7 битов.
Задача 6.
64 числа.Задача 7. 8 подъездов.
Содержание
Слайд 60 Существует и другой способ измерения количества информации –
алфавитный.
Это - измерение количества информации в тексте (символьном сообщении),
составленном из символов некоторого алфавита.К содержанию текста такая мера информации отношения не имеет.
Поэтому такой подход можно назвать объективным, то есть не зависящим от воспринимающего его субъекта.
Слайд 61 Алфавитный подход удобен при подсчете количества информации, хранимого,
передаваемого и обрабатываемого техническими устройствами.
Устройствам нет дела до содержательной
стороны сообщений.Компьютеры, принтеры, модемы работают не с самой информацией а с ее представлением в виде сообщений.
Оценить информационные результаты их работы как полезные или бесполезные может только человек.
Слайд 63
Мощность алфавита
Число символов в алфавите называется мощностью алфавита.
Чем меньше знаков в используемом алфавите, тем длиннее сообщение.
Так,
например, в алфавите азбуки Морзе всего три знака (точка, тире, пауза), поэтому для кодирования каждой русской или латинской буквы нужно использовать несколько знаков, и текст, закодированный по Морзе, будет намного длиннее, чем при обычной записи.Пример:
Сигнал SOS: 3 знака в латинском алфавите;
11 знаков в алфавите Морзе: ··· пауза – – – пауза ···.
Слайд 64 Количество информации, которое несет в тексте каждый символ
(i), вычисляется из уравнения Хартли:
2i = N,
где N –
мощность алфавита.Величину i можно назвать информационным весом символа.
Отсюда следует, что количество информации во всем тексте (I), состоящем из К символов, равно произведению информационного символа на К:
I = i * K.
Эту величину можно назвать информационным объемом текста.
Слайд 65 Какова минимальная мощность алфавита, с помощью которого можно
записывать
(кодировать информацию)?
Слайд 66
Односимвольный алфавит
Сообщение любой длины, использующее односимвольный алфавит, содержит
нулевую информацию.
Доказательство:
Предположим, что используемый алфавит состоит из одного
символа, например, «1».Интуитивно понятно, что сообщить что-либо с помощью единственного символа невозможно.
Но это же доказывается строго с точки зрения алфавитного подхода.
Информационный вес символа в таком алфавите находится из уравнения:
2i = 1
Но поскольку
1 = 20,
то отсюда следует, что
i = 0 бит
Слайд 67
Пример
Представьте себе толстую книгу в 1000 страниц, на
всех страницах которой написаны одни единицы (единственный символ используемого
алфавита).- Сколько информации в ней содержится?
Ответ: Нисколько, ноль.
11111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111
Слайд 68
Минимальная мощность алфавита
Минимальная мощность алфавита, пригодного для передачи
информации, равна 2.
Такой алфавит называется двоичным алфавитом.
Информационный вес символа
в двоичном алфавите легко определить.Поскольку
2i = 2,
то i = 1 бит
Итак, один символ двоичного алфавита несет 1 бит информации.
1 бит – исходная единица измерения информации.
Слайд 69
Мощность русского алфавита
Каждая буква русского алфавита
(если считать,
что е = ё)
несет информацию 5 бит
(32 = 25).
Слайд 70
Компьютерный алфавит
Современный компьютер может обрабатывать числовую, текстовую, графическую,
звуковую и видео информацию.
Все эти виды информации в компьютере
представлены в двоичном коде, т. е. используется алфавит мощностью два (всего два символа 0 и 1).Связано это с тем, что удобно представлять информацию в виде последовательности электрических импульсов: импульс отсутствует (0), импульс есть (1).
Такое кодирование принято называть двоичным, а сами логические последовательности нулей и единиц - машинным языком.
Слайд 71
Байт
Компьютер для внешнего представления текстов и другой символьной
информации использует
алфавит мощностью
256 символов.
Байт вводится как информационный вес символа
из алфавита мощностью 256.Так как
256 = 28,
то 1 байт = 8 бит.
Слайд 72
Производные единицы измерения информации
Килобайт больше байта в 1024
раза, а число 1024 = 210.
При приближенных вычислениях можно
использовать коэффициент 1000.1 Мегабайт (1 Мб) = 1024 Кбайт ≈ 1000 Кб
1 Гигабайт (1Гб) = 1024 Мбайт ≈ 1000 Мб
1 Терабайт (1Тб) = 1024 Гигабайт ≈ 1000 Гб
1 Петабайт (Пб) = 1024 Терабайт ≈ 1000 Тб
Слайд 73
Задачи для закрепления
Задача 1.
Книга, набранная с помощью компьютера,
содержит 159 страниц.
На каждой странице – 40 строк.
В каждой
строе – 60 символов.Каков объем информации в книге?
Решение:
Мощность компьютерного алфавита равна 256.
Один символ несет 1 байт информации.
Значит, страница содержит 40 * 60 = 2400 байт информации.
Объем всей информации в книге (в разных единицах):
2400 * 150 = 360 000 байт
360000/1024 = 351,5625 Кбайт
351,5625/1024 = 0,3433 Мбайт.
Содержание
Слайд 74
Задачи для закрепления
Задача 2.
Объем сообщения, содержащего 2048 символов,
составил 1/512 часть Мбайта.
Каков размер алфавита, с помощью которого
записано сообщение?Решение:
Переведем информационный объем сообщения в биты:
I = 1/512 * 1024 * 1024 * 8 = 16384 бит.
Поскольку такой объем информации несут 1024 символа (К), то на один символ приходится:
i = I/K = 16384/1024 = 16 бит.
Отсюда следует, что размер (мощность) использованного алфавита равен 216 = 65536 символов.
Содержание
Слайд 75
Задачи для самостоятельного решения
Задача 1.
Алфавит племени Мульти состоит
из 8 букв.
Какое количество информации несет одна буква этого
алфавита?Задача 2.
Сообщение, записанное буквами из 64-х символьного алфавита, содержит 20 символов.
Какой объем информации оно несет?
Содержание
Слайд 76
Задачи для самостоятельного решения
Задача 3.
Племя Мульти имеет 32-х
символьный алфавит.
Племя Пульти использует 64-х символьный алфавит.
Вожди племен обменялись
письмами.письмо племени мульти содержало 80 символов, а письмо племени Пульти – 70 символов.
Сравните объем информации, содержащейся в письмах.
Содержание
Слайд 77
Задачи для самостоятельного решения
Задача 4.
Информационное сообщение объемом 1,5
Кбайт содержит 3072 символа.
Сколько символов содержит алфавит, при помощи
которого было записано это сообщение?Задача 5.
Сколько килобайтов составляет сообщение, содержащее 12288 битов?
Содержание
Слайд 78
Задачи для самостоятельного решения
Задача 6.
Сколько килобайтов составит сообщение
из 384 символов 16-ти символьного алфавита?
Задача 7.
Для записи текста
использовался 256-символьный алфавит.Каждая страница содержит 30 строк по 70 символов в строке.
Какой объем информации содержат 5 страниц текста?
Содержание
Слайд 79
Задачи для самостоятельного решения
Задача 8.
Сообщение занимает 3 страницы
по 25 строк.
В каждой строке записано по 60 символов.
Сколько
символов в использованном алфавите, если все сообщение содержит 1125 байтов?Содержание
Слайд 80
Задачи для самостоятельного решения
Задача 9.
Для записи сообщения использовался
64-х символьный алфавит.
Каждая страница содержит 30 строк.
Все сообщение содержит
8775 байтов информации и занимает 6 страниц.Сколько символов в строке?
Содержание





























