Презентация на тему Системы счисления

систем счисления
Позиционные системы счисления
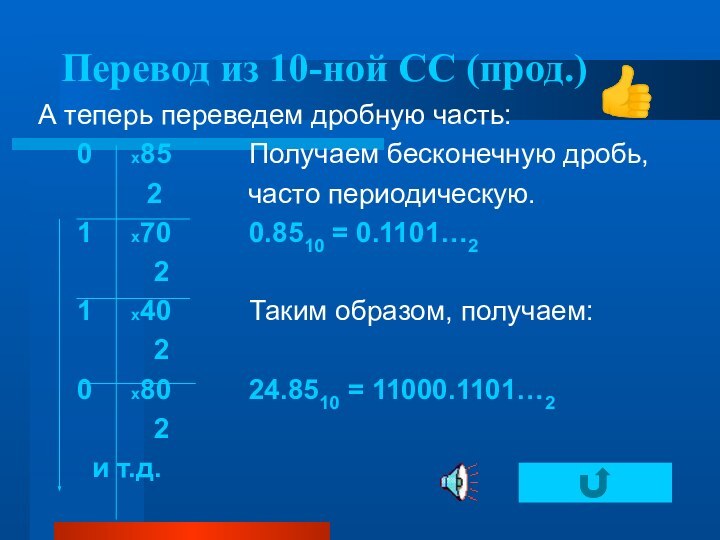
Перевод из 10-тичной СС
Перевод в 10-тичную

СС
Перевод из 2-ной в 8-ную и обратно
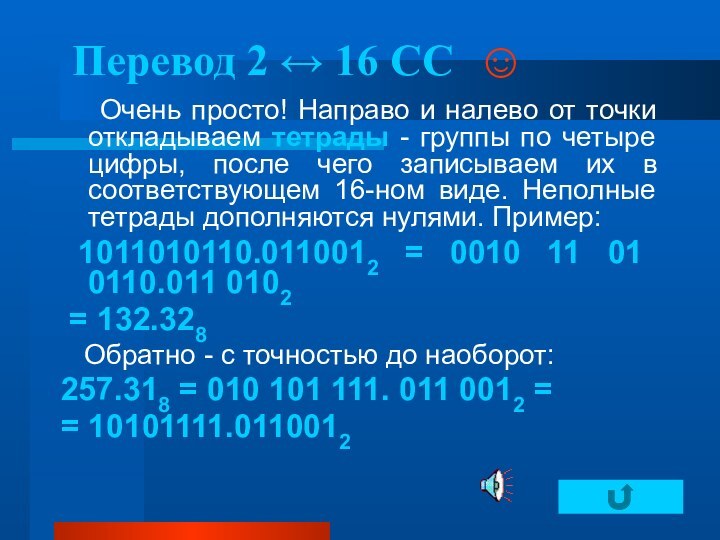
Перевод из 2-ной в 16-ную и обратно
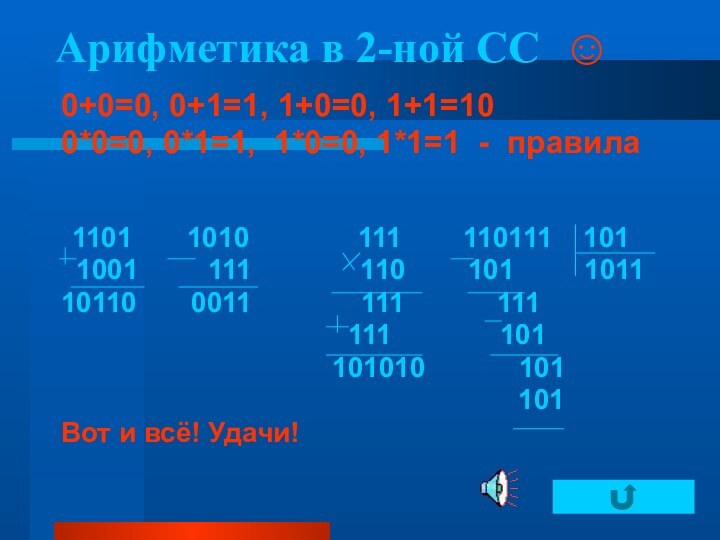
Арифметика в 2-ной СС

считаем от 0 до 9? А как можно считать

еще? Оказывается, существует множество вариантов! И это зависит от такого понятия, как система счисления.
Система счисления – совокупность символов и правил записи с их помощью чисел.

Наши предки поль-зовались пальцами для счета задолго до

того, как научились записывать результаты.

позиционные и непозиционные.
Непозиционная СС – это римская,

когда значение цифры не зависит от её расположения


IV – римская 4,
но I имеет значение 1, а V – значение 5,

VI – римская 6,
но I – всё равно 1,
а V – всё равно 5

от того количества знаков, которое участвует в создании всех

чисел.
Например, 2-ная, 3-ная, 8-ная, 10-ная, 16-ная СС.


А древние вавиловя-не вообще считали в 60-ричной СС!
А записываются позиционные СС с базисом очень просто:
123, 1210, 128 и т.д.

и отдельно для дробной части числа. Переведем, например, число

24.8510 в 2-ную СС.
24 2
0 12 2 2410 = 110002
0 6 2
0 3 2
1 1 

дробную часть:
0 х85

Получаем бесконечную дробь,
2 часто периодическую.
1 х70 0.8510 = 0.1101…2
2
1 х40 Таким образом, получаем:
2
0 х80 24.8510 = 11000.1101…2
2
и т.д.

мы расставляем разряды, потом каждую цифру умножаем на базис

в степени этого разряда. Например, переведем 101001.012 в 10-ную СС:
150413020110.0-11-22 = 125 + 024 +
+ 123 + 022 + 021 + 120 + 02-1 +
+ 12-2 = 32 + 8 + 1 + 0.25 = 41.2510

Направо и налево от точки откладываем триады - группы

по три цифры, после чего записываем их в соответствующем 8-ном виде. Неполные триады дополняются нулями. Пример:
1011010.011012 = 001 011 010.011 0102
= 132.328
Обратно - с точностью до наоборот:
257.318 = 010 101 111. 011 0012 =
= 10101111.0110012

просто! Направо и налево от точки откладываем тетрады -

группы по четыре цифры, после чего записываем их в соответствующем 16-ном виде. Неполные тетрады дополняются нулями. Пример:
1011010110.0110012 = 0010 11 01 0110.011 0102
= 132.328
Обратно - с точностью до наоборот:
257.318 = 010 101 111. 011 0012 =
= 10101111.0110012