- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Колодец Лотоса
Содержание
- 2. ЗАГАДКА ИЗ ДРЕВНЕГО ЕГИПТА
- 3. В 1912 г. во время раскопок в
- 4. "Ты стоишь перед стеной, за ней колодец
- 5. Под текстом задачи было обнаружено пояснение, из
- 6. Наиболее известным источником сведений, связанных с этой
- 7. Хатшепсут была единственной в истории Египта женщиной-фараоном.
- 8. Задача о Колодце Лотоса
- 9. В рассказе предложен один из вариантов решения
- 10. Задачу о колодце Лотоса интересно было бы решить в соответствии с уровнем древней математики.
- 11. Пусть AС = 3, BD= 2, EF
- 12. Теорема. Длина отрезка, концы которого лежат
- 13. Для египтянина естественно было искать решение задач
- 14. Обе эти дроби хорошо соответствуют духу египетской
- 15. Значение диаметров занесем в таблицу:Заметим, что число
- 16. Скачать презентацию
- 17. Похожие презентации
ЗАГАДКА ИЗ ДРЕВНЕГО ЕГИПТА







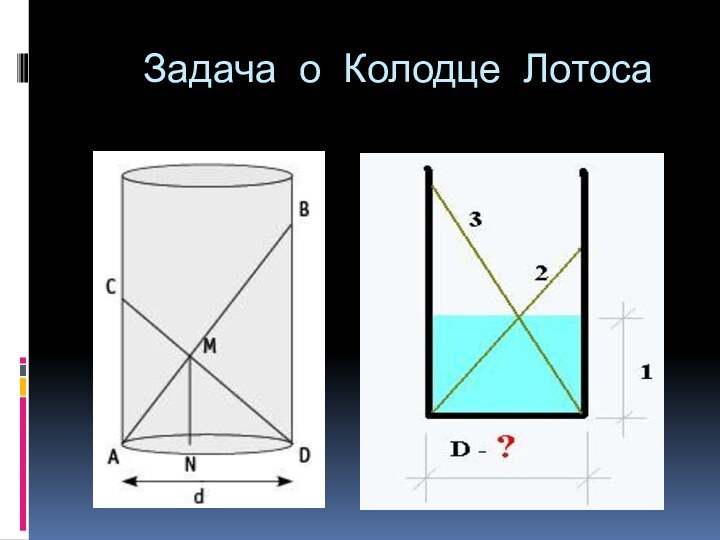







Слайд 4 "Ты стоишь перед стеной, за ней колодец Лотоса,
круглый, как Солнце. В колодец опущены два тростниковых стебля,
длина одного из которых три меры, другого — две меры. Стебли перекрещиваются на уровне поверхности воды, а уровень воды в колодце равен одной мере. Кто укажет длину самой длинной прямой, которая может уместиться в основании колодца Лотоса, тот возьмет тростниковые стебли и станет жрецом бога Ра".
Слайд 5
Под текстом задачи было обнаружено пояснение, из которого
следует, что она служила испытанием для желающих стать жрецами
бога Ра.Вошедший в комнату для решения этой задачи оказывался отрезан от внешнего мира, так что решивший ее становился жрецом, а не решивший умирал голодной смертью.
"Через стену колодца Лотоса прошли многие, но мало кто стал жрецом бога Ра. Думай. Цени свою жизнь. Так советуют тебе жрецы бога Ра".
Слайд 6 Наиболее известным источником сведений, связанных с этой задачей,
является рассказ писателя-фантаста А.П.Казанцева «Колодец Лотоса».
Это история любви
могущественной древнеегипетской царицы Хапшетсут и придворного зодчего Сененмута. Слайд 7 Хатшепсут была единственной в истории Египта женщиной-фараоном. Ей
воздавались все подобающие фараонам светские и религиозные почести, ее
изображали, как и полагалось настоящему фараону, с привязанной под подбородком бородой.В рассказе А.П. Казанцева Хатшепсут решает сделать Сененмута жрецом, для чего он должен пройти загадочное испытание.
Слайд 9 В рассказе предложен один из вариантов решения задачи,
доступный кандидатам на звание жреца.
После довольно замысловатых манипуляций,
использующих мокрые части тростинок, Сененмуту удается получить приближенное значение диаметра колодца d, равное 37/30.Слайд 10 Задачу о колодце Лотоса интересно было бы решить
в соответствии с уровнем древней математики.
Слайд 11 Пусть AС = 3, BD= 2, EF =
1,
требуется определить ВС.
Обозначим АВ = a, CD
= b ,ВС = d .
Путем несложных преобразований получаем уравнение
a4 - 2а3 + 5а2 -10а + 5 = 0
Однако в Древнем Египте
не умели решать уравнений 4-й степени!
Слайд 12 Теорема. Длина отрезка, концы которого лежат на
боковых сторонах трапеции, а сам он параллелен ее основаниям
и проходит через точку пересечения диагоналей, равна среднему гармоническому длин оснований трапеции:МN = 2аb : (а + b)
Кроме того,
точка пересечения диагоналей делит данный отрезок пополам:
МО = ab : (а + b)
Слайд 13
Для египтянина естественно было искать решение задач в
виде дробей с малыми знаменателями.
Если рассматривать дробные числа
со знаменателями не более 5, то неплохое приближение диаметра колодца дают дроби 5/4 и 6/5. Слайд 14 Обе эти дроби хорошо соответствуют духу египетской математики,
где было принято записывать произвольную дробь в виде суммы
дробей с числителями, равными 1:5 1 6 1
— = 1 + —, — = 1+ — .
4 4 5 5
Слайд 15
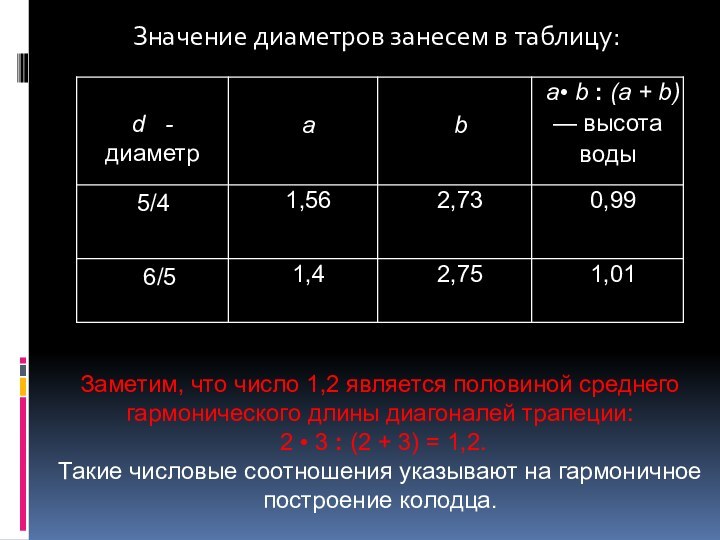
Значение диаметров занесем в таблицу:
Заметим, что число 1,2
является половиной среднего гармонического длины диагоналей трапеции:
2 •
3 : (2 + 3) = 1,2. Такие числовые соотношения указывают на гармоничное построение колодца.