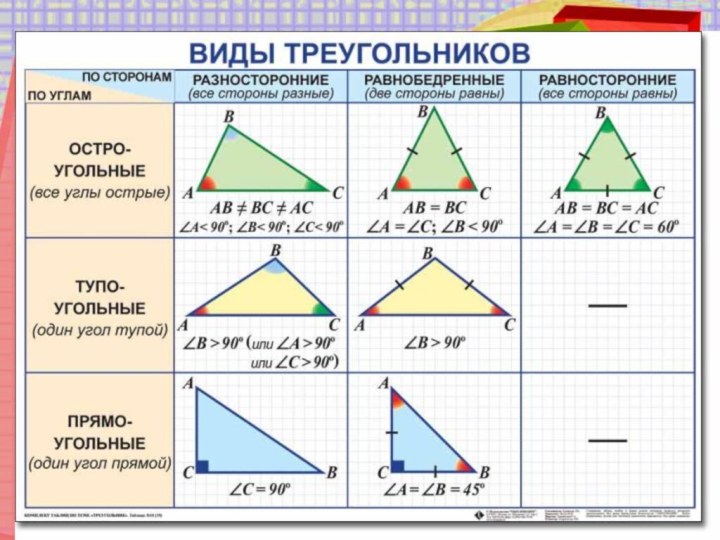
по теме;
Повторить способы решения задач на
нахождение элементов и
площадей треугольника;Рассмотреть способы решения прикладных и
старинных задач.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть




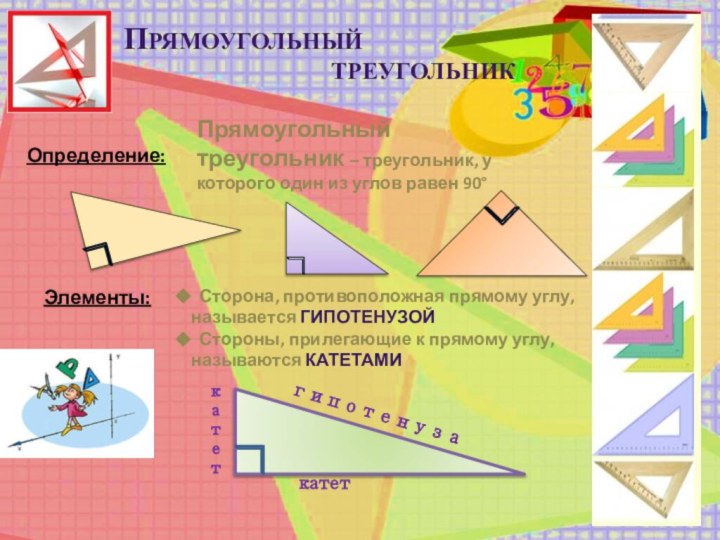
















Элементы:
Сторона, противоположная прямому углу, называется гипотенузой
Стороны, прилегающие к прямому углу, называются катетами
гипотенуза
к
а
т
е
т
катет
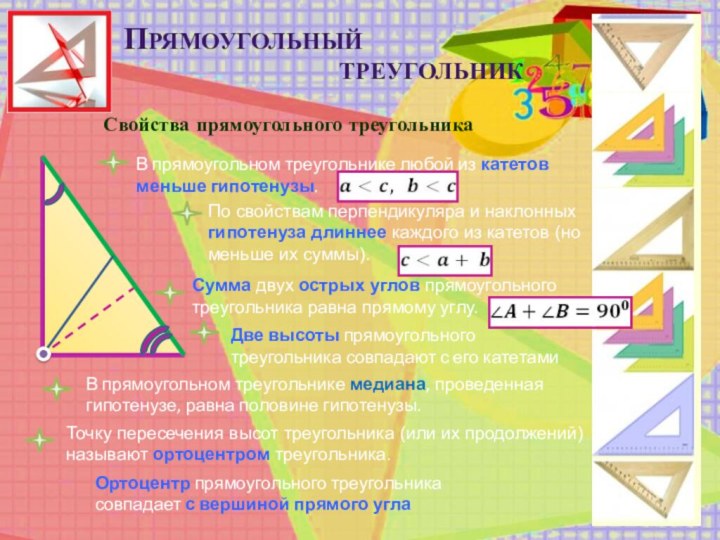
В прямоугольном треугольнике любой из катетов меньше гипотенузы.
Сумма двух острых углов прямоугольного треугольника равна прямому углу.
По свойствам перпендикуляра и наклонных гипотенуза длиннее каждого из катетов (но меньше их суммы).
Две высоты прямоугольного треугольника совпадают с его катетами
Точку пересечения высот треугольника (или их продолжений) называют ортоцентром треугольника.
Ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
А
В
С
В
А
С
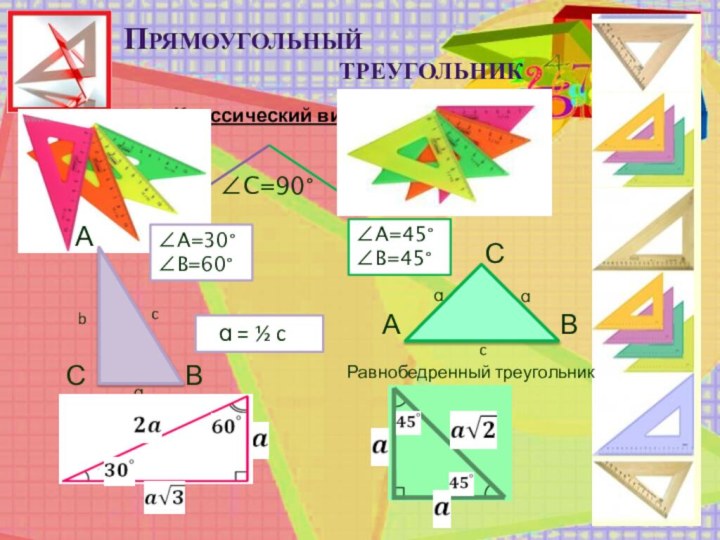
ɑ = ½ c
∠A=30°
∠B=60°
ɑ
c
∠C=90°
∠A=45°
∠B=45°
Равнобедренный треугольник
c
ɑ
ɑ
b
ПРЯМОУГОЛЬНЫЙ
ТРЕУГОЛЬНИК
Окружность, вписанная в треугольник
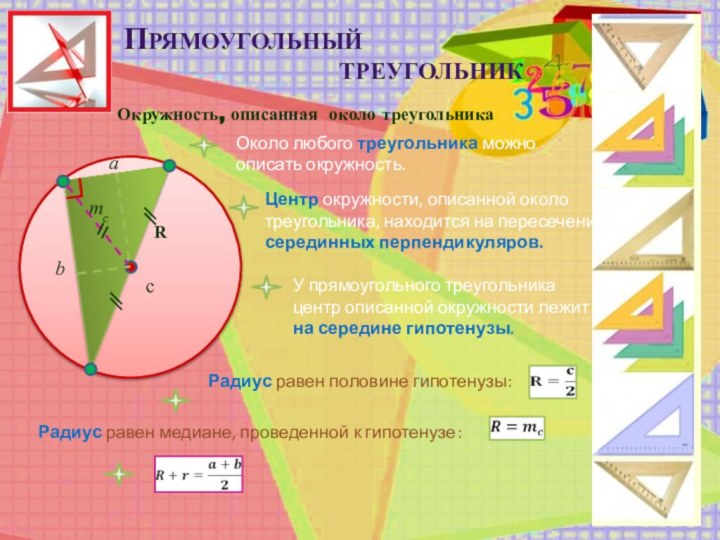
Около любого треугольника можно описать окружность.
Центр окружности, описанной около треугольника, находится на пересечении серединных перпендикуляров.
У прямоугольного треугольника центр описанной окружности лежит на середине гипотенузы.
Радиус равен половине гипотенузы:
Радиус равен медиане, проведенной к гипотенузе:
a
b
c
mc
R
H
B
H
B
A
C
H
B
A
C
A
C
Высота прямоугольного треугольника, проведенная из
вершины прямого угла, разделяет треугольник на два
подобных прямоугольных треугольника, каждый из
которых подобен данному треугольнику.
ПРЯМОУГОЛЬНЫЙ
ТРЕУГОЛЬНИК
Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен
сумме квадратов катетов.
Если длины всех трёх сторон прямоугольного треугольника являются целыми числами, то треугольник называется пифагоровым треугольником, а длины его сторон образуют так называемую
(3, 4, 5),
(6, 8, 10),
(5, 12, 13),
(9, 12, 15),
(8, 1, 17),
(12, 16, 20),
(15, 20, 25),
(7, 24, 25),
(10, 24, 26),
(20, 21, 29)
(18, 24, 30),
(16, 30, 34),
(21, 28, 35),
(12, 35, 37),
(15, 36, 39),
(24, 32, 40),
(9, 40, 41),
(27, 36, 45),
(14, 48, 50),
(30, 40, 50), …
пифагорову тройку
B
C
A
A
B
C
Равнобедренный прямоугольный треугольник
ɑ
ɑ
ɑ
c
c
b
h
- высота из прямого угла
a, b - катеты
с - гипотенуза
bc , ac - отрезки полученные от деления гипотенузы, высотой
α, β - углы при гипотенузе
hc
Формула длины высоты через стороны
Формула длины высоты через гипотенузу
и острые углы
Формула длины высоты
через катет и угол
Формула длины высоты через составные отрезки гипотенузы
Высота прямоугольного треугольника,
проведенная из вершины прямого угла, есть среднее пропорциональное
(геометрическое) для отрезков, на которые делится гипотенуза этой высотой.
Катет прямоугольного треугольника
есть среднее пропорциональное для гипотенузы и отрезка
гипотенузы, заключенного между катетом и высотой,
проведенной из вершины прямого угла.
B
A
C
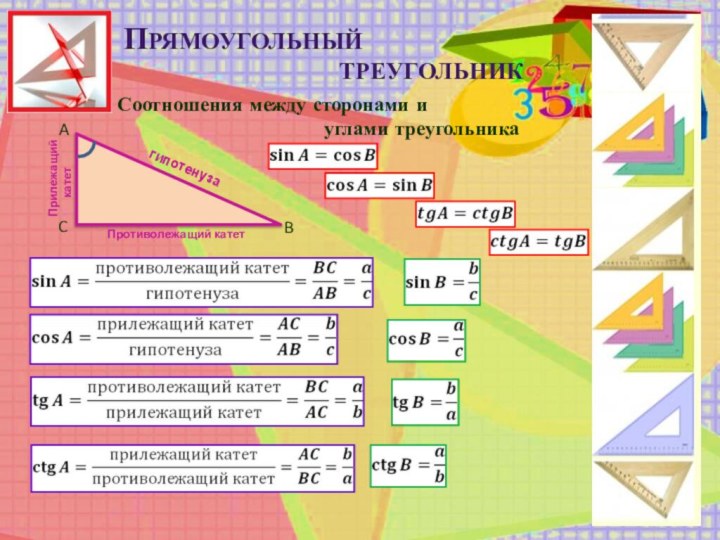
Противолежащий катет
гипотенуза
Прилежащий
катет