- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Параллельность прямых и плоскостей
Содержание
- 2. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.ОпределениеМab
- 3. IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIiНаглядное представление о скрещивающихся прямых дают две
- 4. ab
- 5. Найдите на рисунке параллельные прямые.Назовите параллельные прямые и плоскости.Найдите скрещивающиеся прямые.
- 6. Если одна из двух прямых лежит в
- 7. а II bТри случая взаимного расположения двух прямых в пространствеМababab
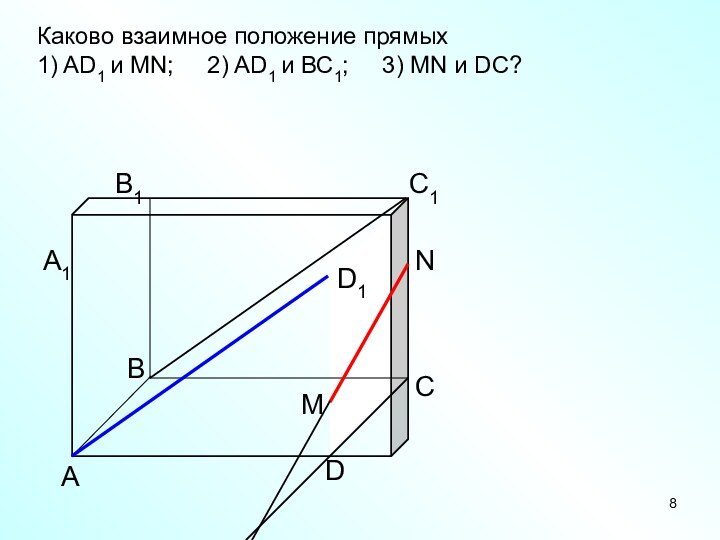
- 8. АDСВB1С1D1А1Каково взаимное положение прямых1) AD1 и МN;
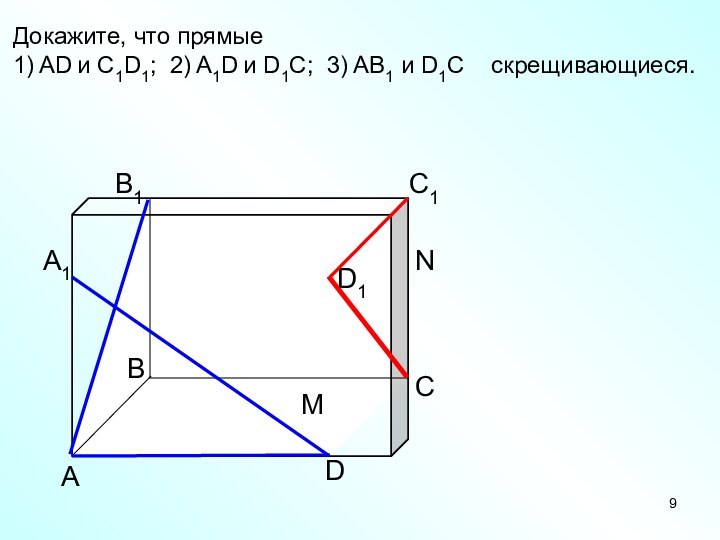
- 9. АDСВB1С1D1А1Докажите, что прямые 1) AD и C1D1;
- 10. АDСВB1С1D1А1Основание призмы АВСDA1B1C1D1 – трапеция. Какие из
- 11. Через каждую из двух скрещивающихся прямых проходит
- 12. полуплоскостьполуплоскостьграницаЛюбая прямая а, лежащая в плоскости, разделяет
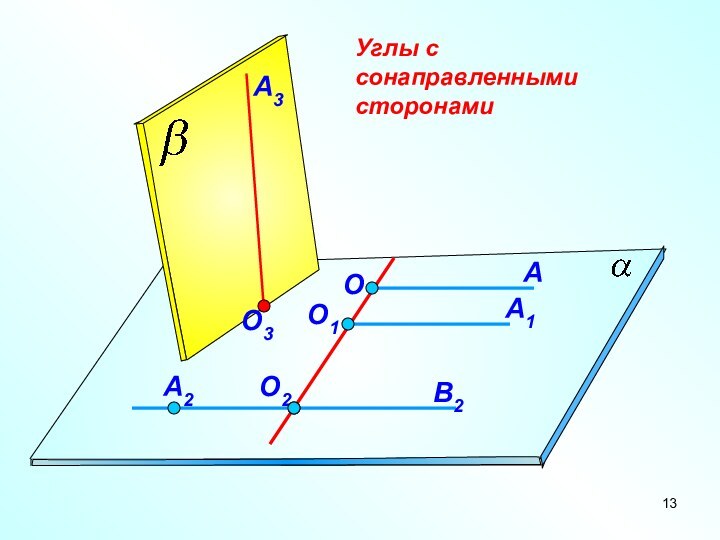
- 13. Углы с сонаправленными сторонамиAОО1О2A1В2A2О3A3
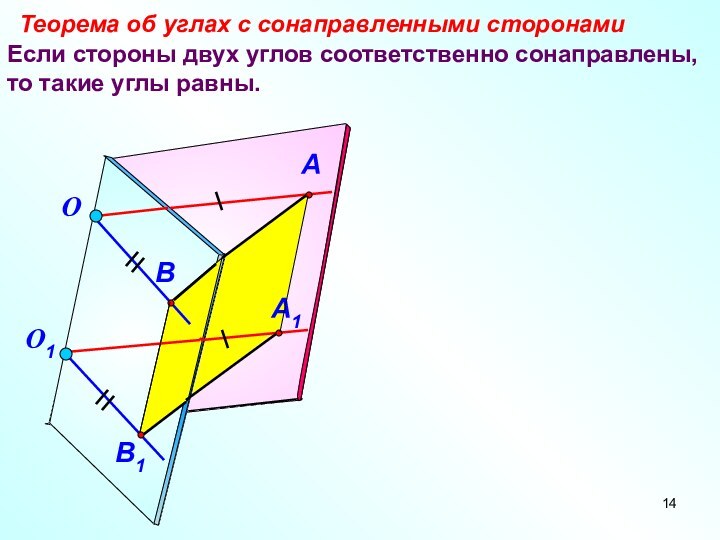
- 14. Если стороны двух углов соответственно сонаправлены, то такие углы равны.Теорема об углах с сонаправленными сторонами
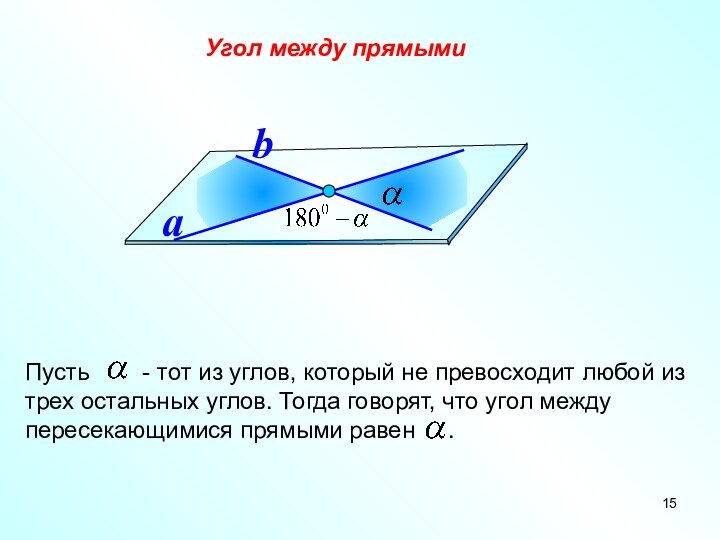
- 15. Угол между прямымиab
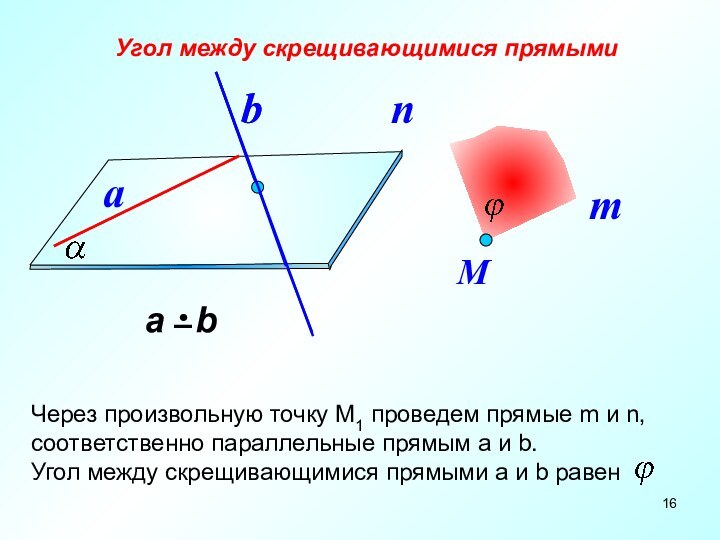
- 16. Угол между скрещивающимися прямымиabbМ
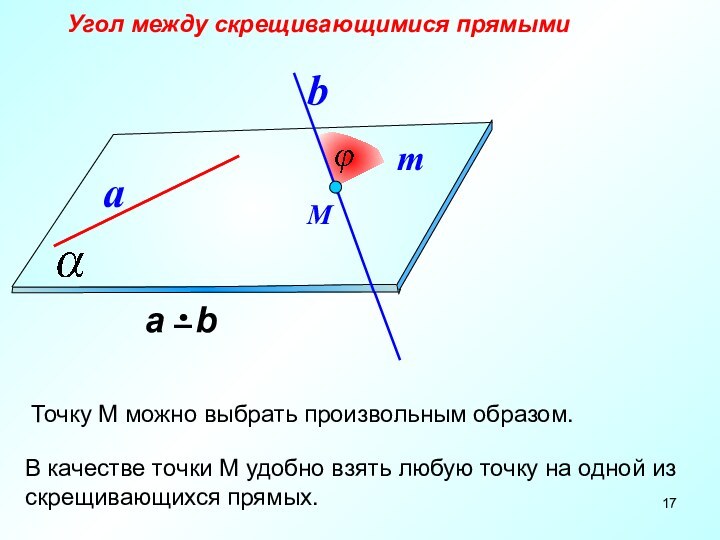
- 17. Угол между скрещивающимися прямымиabМ Точку М можно
- 18. Три случая взаимного расположения прямой и плоскостиПрямая
- 19. Параллельность прямой и плоскости
- 20. Наглядное представление о прямой, параллельной плоскости, дают
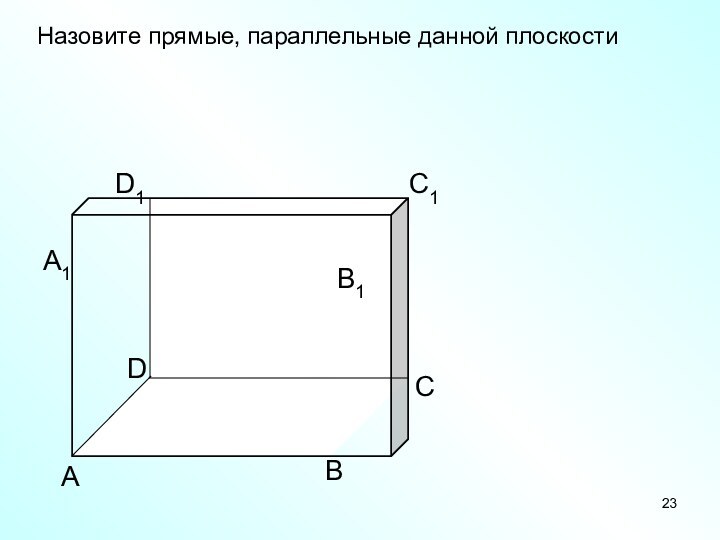
- 23. АВСDD1С1В1А1Назовите прямые, параллельные данной плоскости
- 24. ab ТеоремаЕсли прямая не лежащая
- 25. Следствие 10Если плоскость проходит через данную прямую,
- 26. Следствие 20Если одна из двух параллельных прямых
- 27. МАВbamnПрямые m и n пресекаются в точке
- 28. МАВbamnПрямые m и n пресекаются в точке
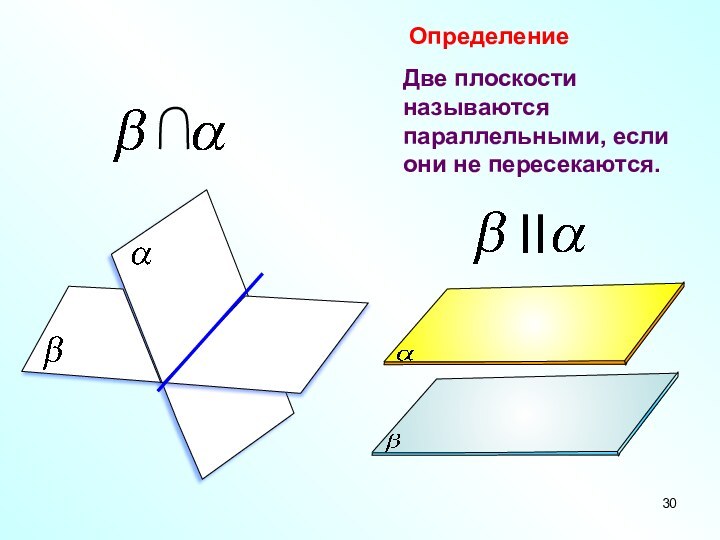
- 29. Параллельность плоскостей
- 34. Если две пересекающиеся прямые одной плоскости параллельны
- 35. №51Если две пересекающиеся прямые m и n
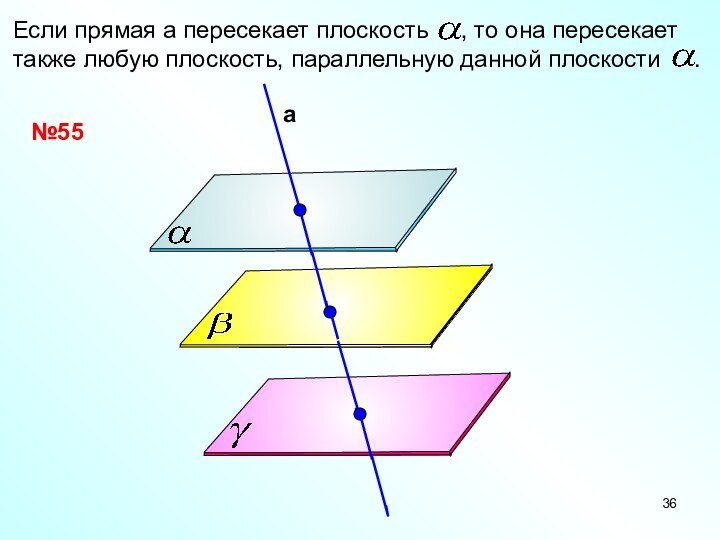
- 36. №55
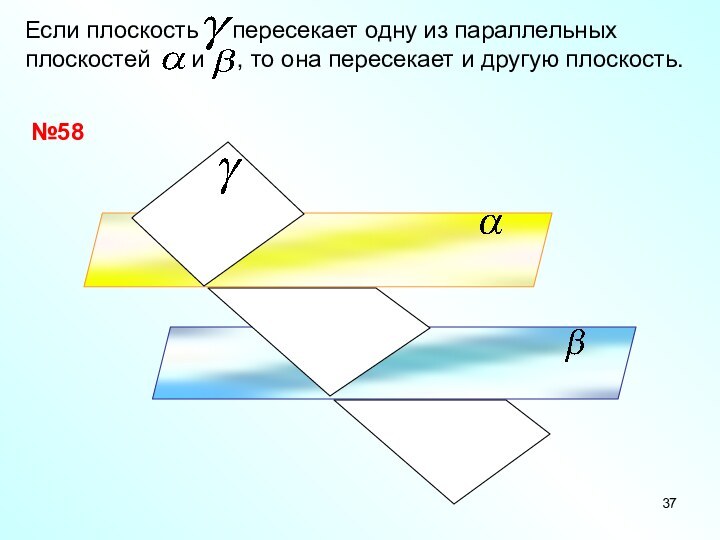
- 37. №58
- 38. №60Если две плоскости и
- 39. Если две параллельные плоскости
- 40. Скачать презентацию
- 41. Похожие презентации
Две прямые называются скрещивающимися, если они не лежат в одной плоскости.ОпределениеМab

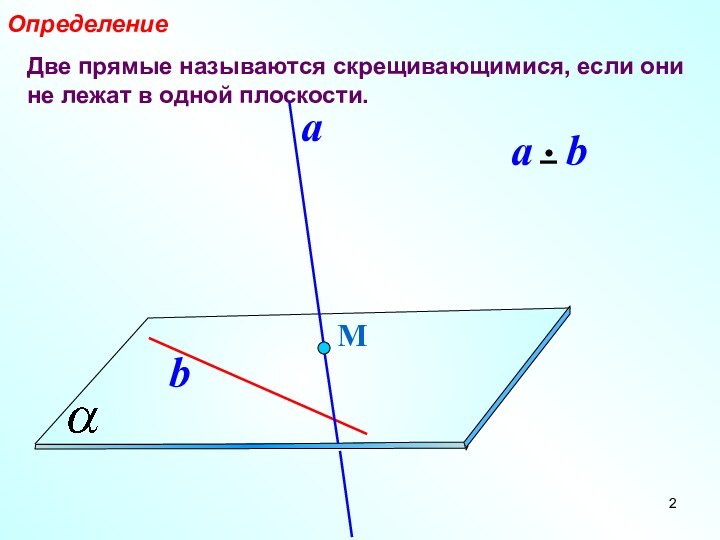






Слайд 3
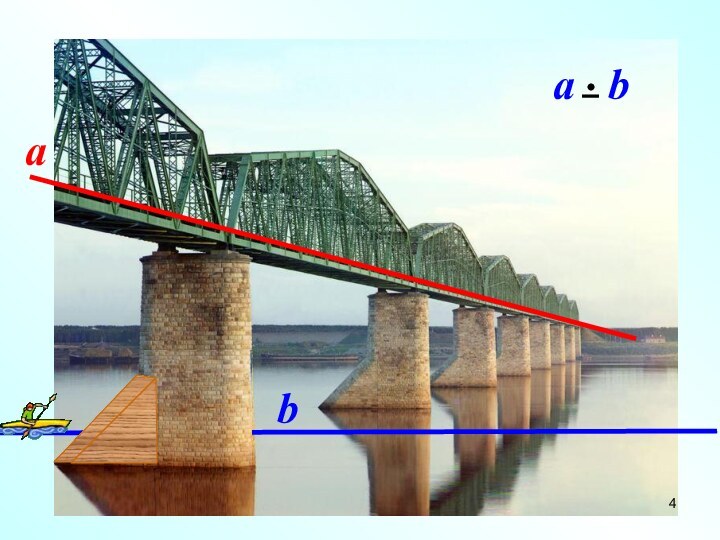
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIi
Наглядное представление о скрещивающихся прямых дают две дороги,
одна из которых проходит по эстакаде, а другая под
эстакадой.
Слайд 5
Найдите на рисунке параллельные прямые.
Назовите параллельные прямые и
плоскости.
Найдите скрещивающиеся прямые.
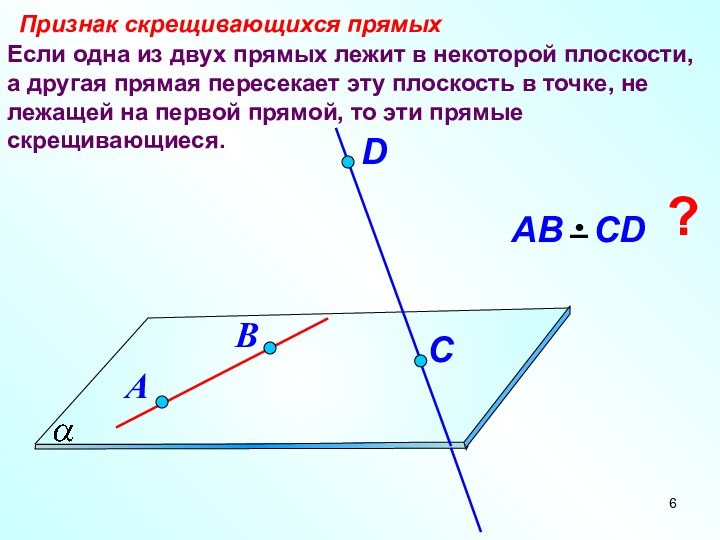
Слайд 6 Если одна из двух прямых лежит в некоторой
плоскости, а другая прямая пересекает эту плоскость в точке,
не лежащей на первой прямой, то эти прямые скрещивающиеся.Признак скрещивающихся прямых
D
В
А
C
?
Слайд 10
А
D
С
В
B1
С1
D1
А1
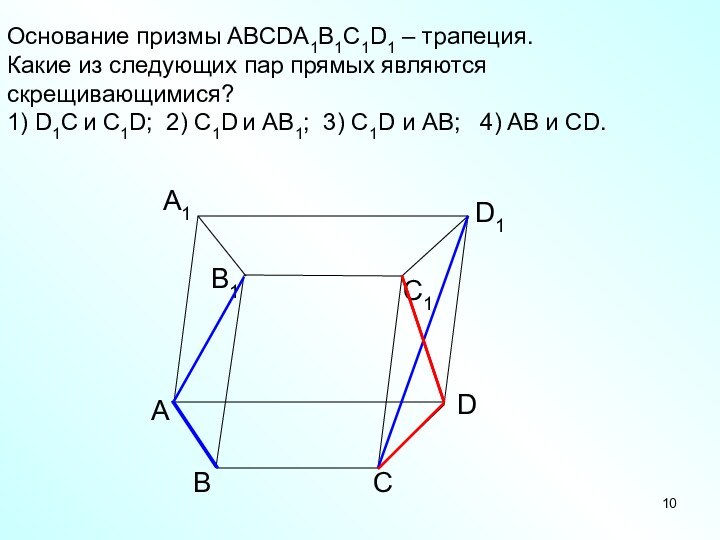
Основание призмы АВСDA1B1C1D1 – трапеция.
Какие из следующих
пар прямых являются
скрещивающимися?
1) D1C и C1D; 2) C1D
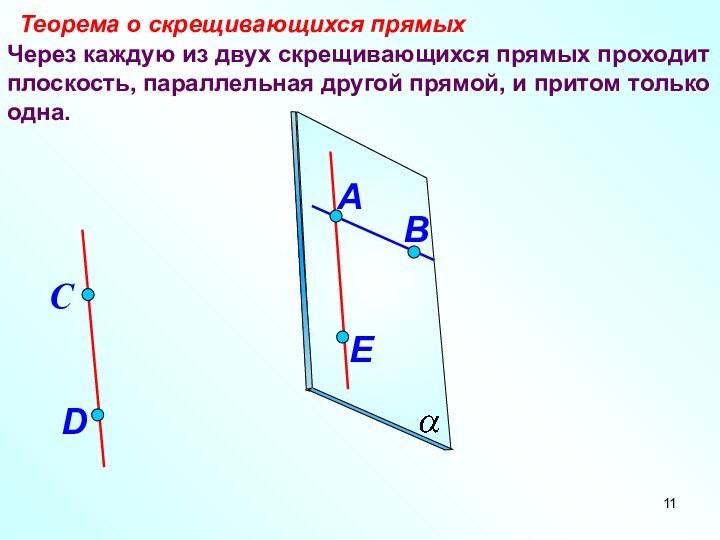
и AB1; 3) C1D и AB; 4) AB и CD.Слайд 11 Через каждую из двух скрещивающихся прямых проходит плоскость,
параллельная другой прямой, и притом только одна.
Теорема о скрещивающихся
прямыхD
С
B
A
Слайд 12
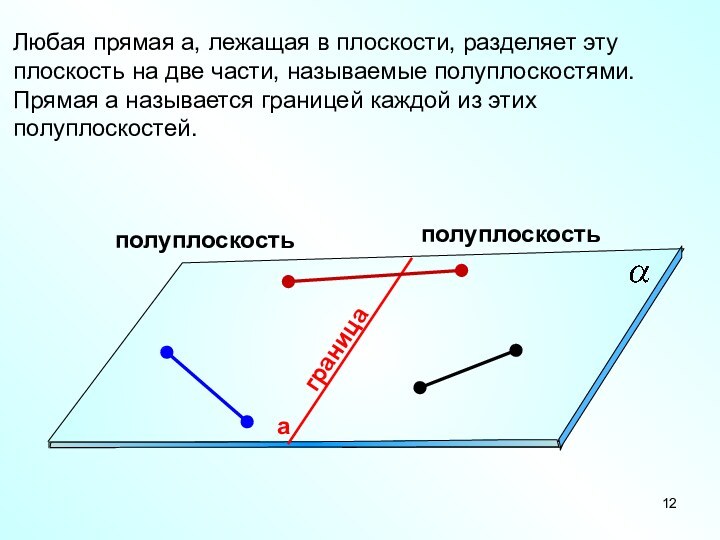
полуплоскость
полуплоскость
граница
Любая прямая а, лежащая в плоскости, разделяет эту
плоскость на две части, называемые полуплоскостями. Прямая а называется
границей каждой из этих полуплоскостей.а
Слайд 14
Если стороны двух углов соответственно сонаправлены, то такие
углы равны.
Теорема об углах с сонаправленными сторонами
Слайд 17
Угол между скрещивающимися прямыми
a
b
М
Точку М можно выбрать
произвольным образом.
m
В качестве точки М удобно взять
любую точку на одной из скрещивающихся прямых.
Слайд 18
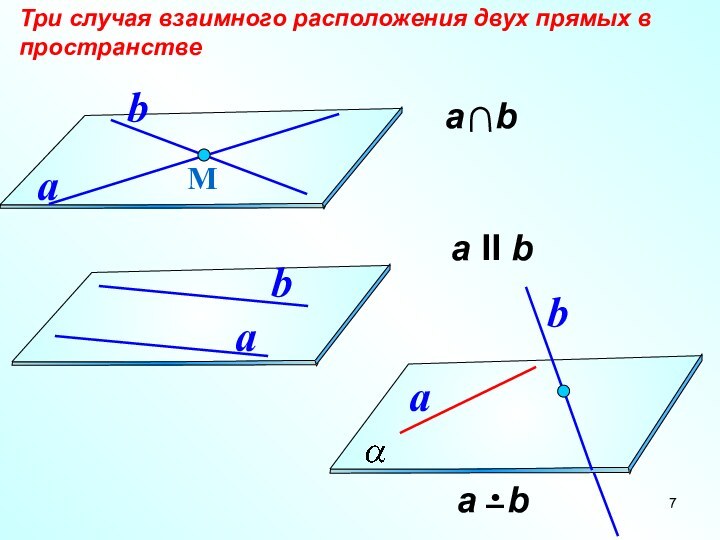
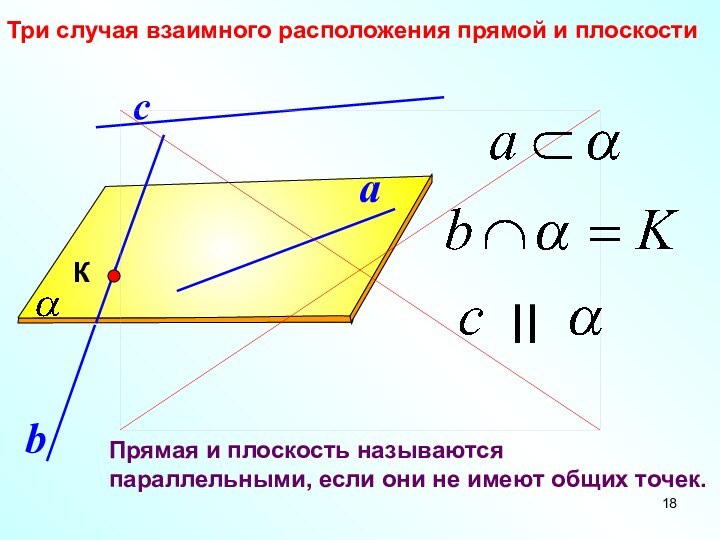
Три случая взаимного расположения прямой и плоскости
Прямая и
плоскость называются параллельными, если они не имеют общих точек.
Слайд 20
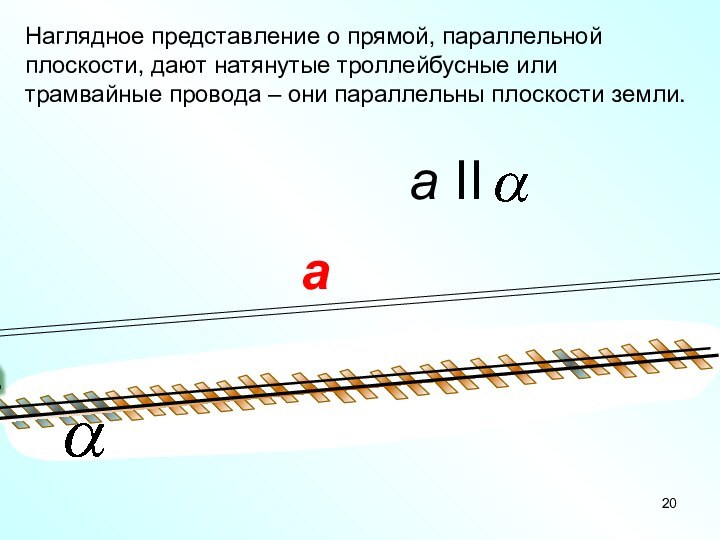
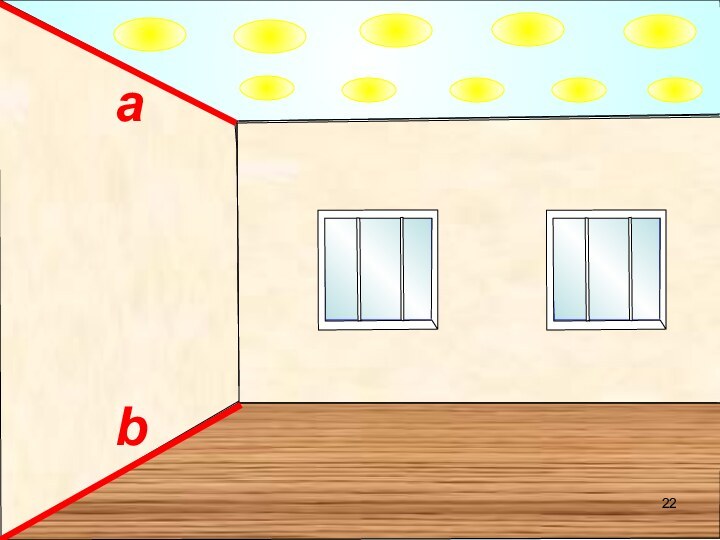
Наглядное представление о прямой, параллельной плоскости, дают натянутые
троллейбусные или трамвайные провода – они параллельны плоскости земли.
Слайд 24
a
b
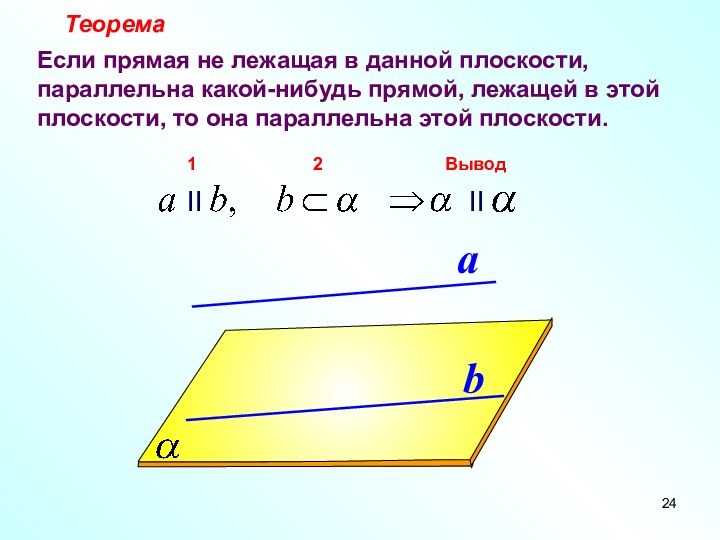
Теорема
Если прямая не лежащая в
данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости,
то она параллельна этой плоскости.
Слайд 25
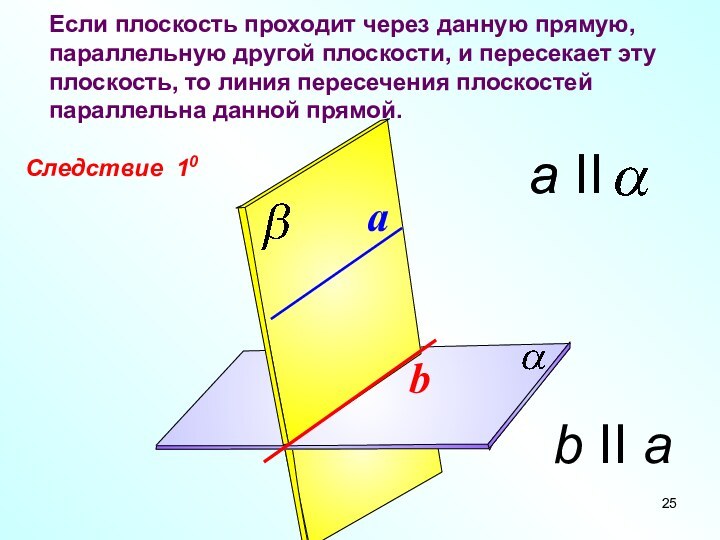
Следствие 10
Если плоскость проходит через данную прямую, параллельную
другой плоскости, и пересекает эту плоскость, то линия пересечения
плоскостей параллельна данной прямой.a
b II a
Слайд 26
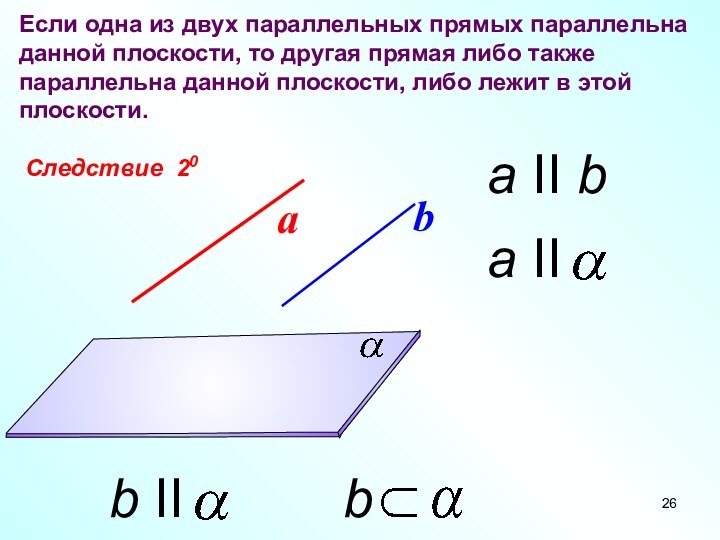
Следствие 20
Если одна из двух параллельных прямых параллельна
данной плоскости, то другая прямая либо также параллельна данной
плоскости, либо лежит в этой плоскости.a II b
Слайд 27
М
А
В
b
a
m
n
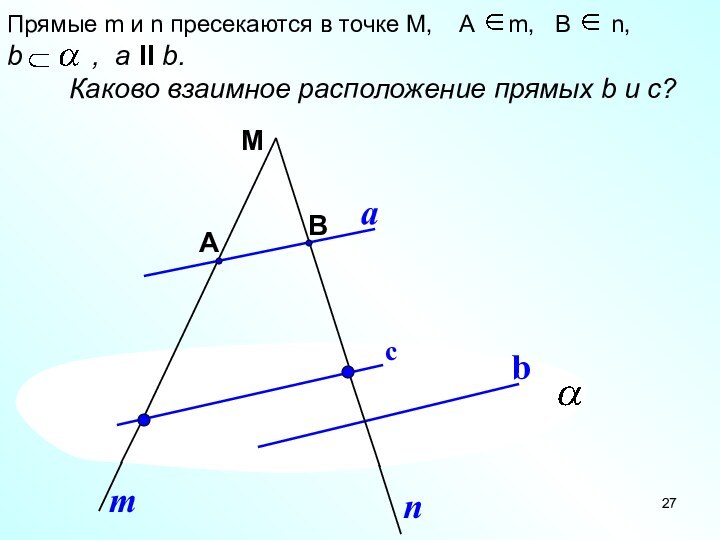
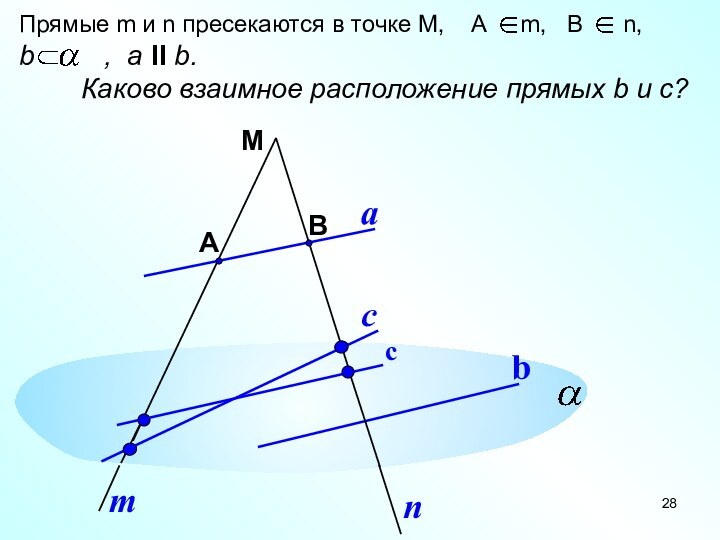
Прямые m и n пресекаются в точке М,
А m, B
n,b , a II b.
Каково взаимное расположение прямых b и c?
Слайд 28
М
А
В
b
a
m
n
Прямые m и n пресекаются в точке М,
А m, B
n,b , a II b.
Каково взаимное расположение прямых b и c?
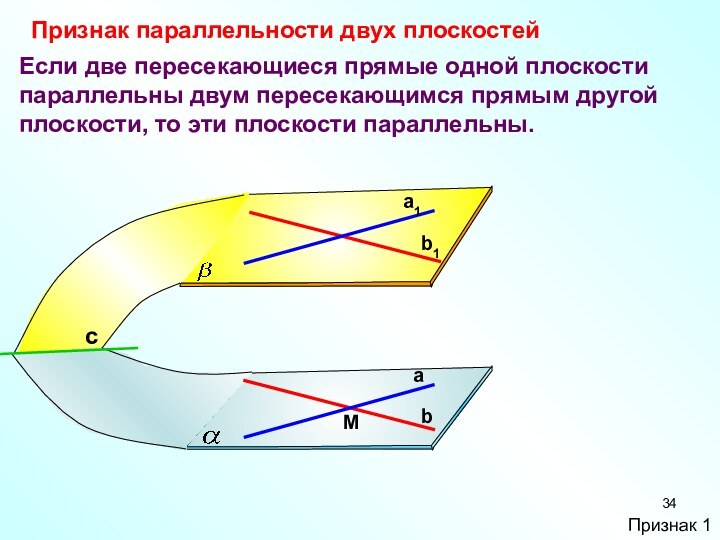
Слайд 34 Если две пересекающиеся прямые одной плоскости параллельны двум
пересекающимся прямым другой плоскости, то эти плоскости параллельны.
Признак параллельности
двух плоскостей M
с
Признак 1
Слайд 35
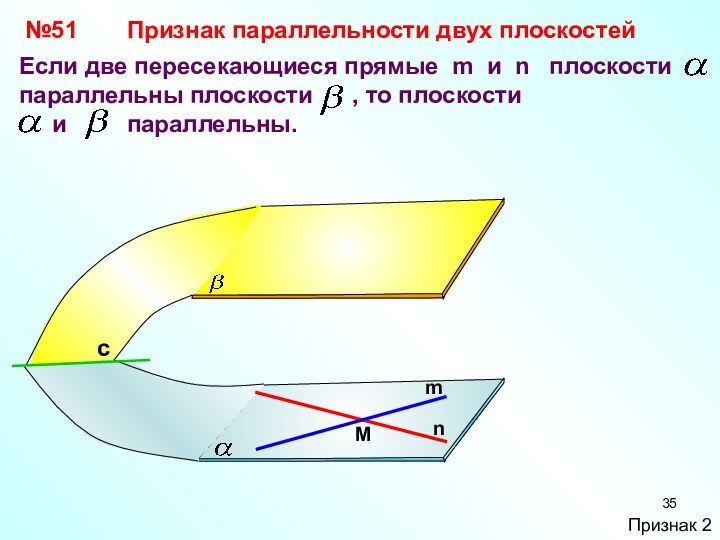
№51
Если две пересекающиеся прямые m и n
плоскости параллельны плоскости ,
то плоскостии параллельны.
Признак параллельности двух плоскостей
n
m
M
с
Признак 2
Слайд 38
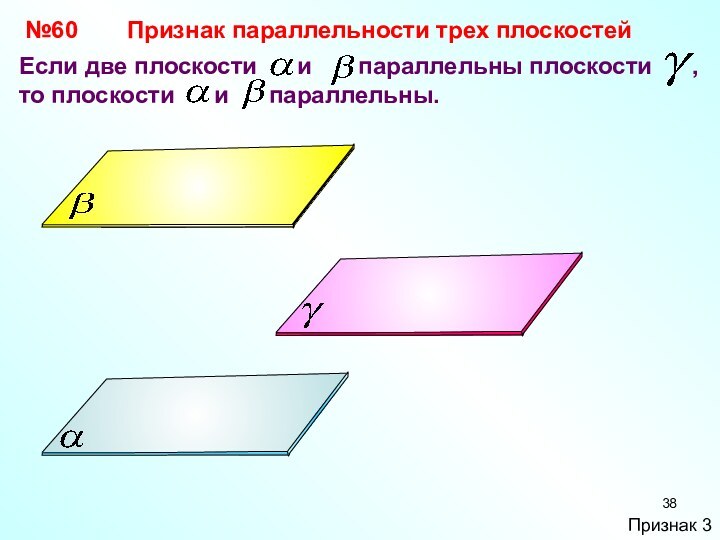
№60
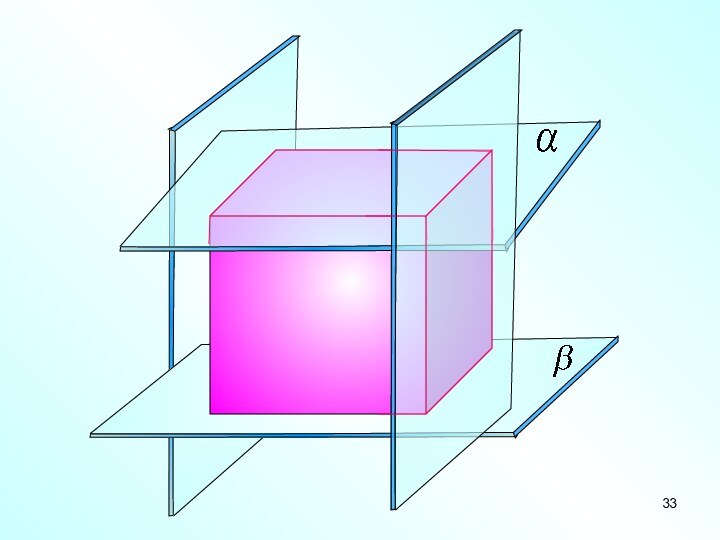
Если две плоскости и
параллельны плоскости , то плоскости
и параллельны.Признак параллельности трех плоскостей
Признак 3
Слайд 39
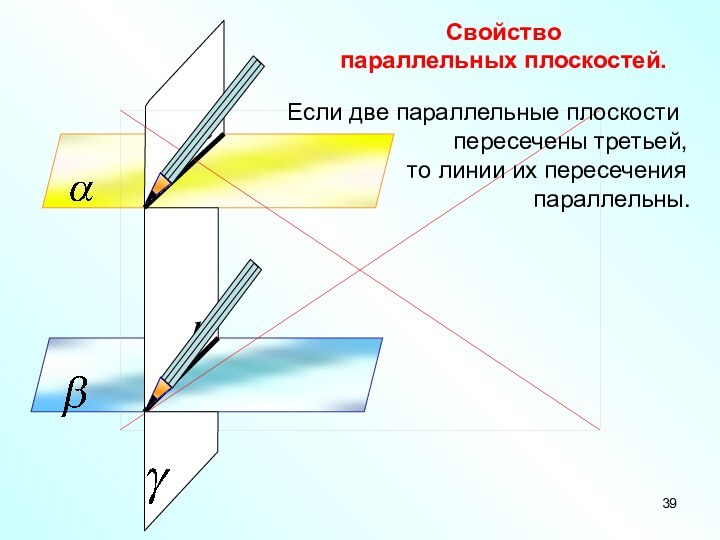
Если две параллельные плоскости
пересечены третьей,
то линии их пересечения
параллельны.
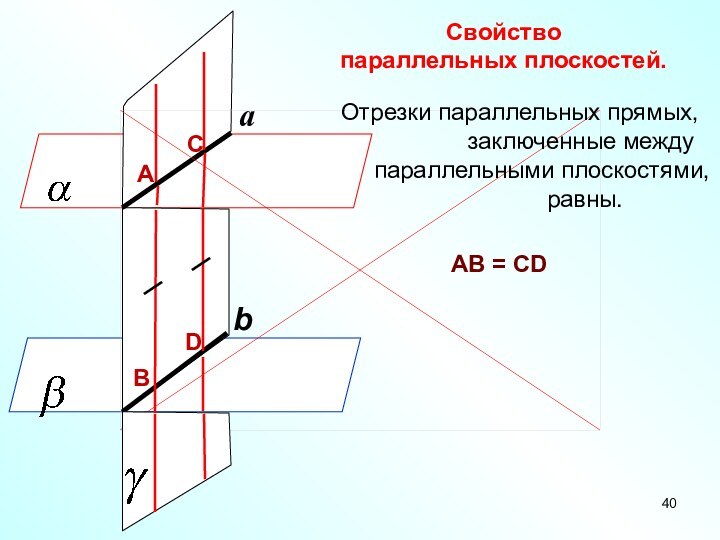
Свойство
параллельных плоскостей.