- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Что такое процент?
Содержание
- 2. Знакомство с процентом. На примерах из жизни познать значимость и необходимость процента.Цель презентации.
- 3. Для чего и когда появился процент?Знакомство с
- 4. Слово «процент» произошло от латинских слов pro
- 5. Идея выражения частей целого постоянно в одних
- 6. Долгое время под процентами понимались исключительно прибыль
- 7. Процент – это частный вид десятичных дробей,
- 8. Если часть величины, заданную десятичной дробью, надо
- 9. Чтобы выразить в процентах часть величины, заданную
- 10. Запомни! Например, 17 % от 500 кг означает
- 11. В 1685 году в Париже была издана
- 12. В тексте знак процента используется только при
- 13. Ударение в слове процент в единственном и
- 14. в) Если зависимое слово по смыслу связано
- 15. Иногда применяют и более мелкие доли целого
- 16. Величина в промилле от массы, выраженной в
- 17. Поскольку проценты выражаются дробями, то задачи на
- 18. Какого количество В, Р % от которого
- 19. Какого количество В, большее (меньшее) чем А,
- 20. Сколько % составляет А от В? Нахождение
- 21. На сколько % А больше (меньше), чем
- 22. Задача 1. В январе стоимость билета в
- 23. Cначала узнаём, на сколько рублей подорожал билет
- 24. Задача 2. За хорошую учебу своего сына
- 25. 20 000•5/100 = 1000 руб. – составляют
- 26. Задача 3. Собрали 100 кг грибов. Оказалось,
- 27. По условию в 100 кг грибов содержится
- 28. Напоследок мне хочется рассмотреть заинтересовавшие меня проценты,
- 29. Если проценты на депозит начисляются один раз
- 30. Пример 1. Банком принят депозит в сумме
- 31. Если проценты на депозит начисляются несколько раз
- 32. Пример 1. Принят депозит в сумме 100
- 33. Я повторил пройдённый материал по процентам. Познакомился
- 34. Скачать презентацию
- 35. Похожие презентации

































Слайд 3
Для чего и когда появился процент?
Знакомство с процентом.
Происхождение
обозначения.
Правила набора.
Знакомьтесь родственник процента – промилле.
Виды задач на проценты
с примерами.Немного житейских задач.
Расчет процентов на банковский депозит. Формула расчета простых процентов.
Расчет процентов на банковский депозит при начислении процента на процент. Формула расчета сложных процентов.
Заключение
Содержание.
Слайд 4
Слово «процент» произошло от латинских слов
pro centum,
что буквально означает «за сотню» или «со ста». Проценты
дают возможность легко сравнивать между собой части целого, упрощая расчёты.Пример: Что больше ½ или ¾?
Для чего и когда появился процент?
½ = 50 % < ¾ = 75 %
Слайд 5 Идея выражения частей целого постоянно в одних и
тех же долях, вызванная практическими соображениями, родилась еще в
древности у вавилонян. Ряд задач клинописных табличек посвящен исчислению процентов, однако вавилонские ростовщики считали не «со ста», а «с шестидесяти», так как в Вавилоне пользовались шестидесятеричными дробями. Проценты были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. От римлян проценты перешли к другим народам Европы.Слайд 6 Долгое время под процентами понимались исключительно прибыль или
убыток на каждые сто рублей. Они применялись только в
торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, в экономических расчетах, в страховании, статистике, науке и технике.В процентах выражаются ставки налогов, доходность капиталовложений, плата за заемные денежные средства (например, кредиты банка), темпы роста экономики и многое другое.
Римляне брали с должника лихву (т. е. деньги сверх того, что дали в долг). При этом говорили: «На каждые 100 сестерциев долга заплатить 16 сестерциев лихвы».
Слайд 7 Процент – это частный вид десятичных дробей, сотая
доля целого (принимаемого за единицу) или сотая часть единицы.
Обозначается знаком «%». Используется для обозначения доли чего-либо по отношению к целому.Запись 1% означает 0,01 или 1/100.
Так как 1 % равен сотой части величины,
то вся величина равна 100%
Знакомство с процентом.
Слайд 8
Если часть величины, заданную десятичной дробью, надо выразить
в процентах, то можно в этой дроби перенести запятую
на два знака вправо и к полученному числу приписать знак %. Справедливо и обратное правило.0,07 % = 0,0007; 0,451 = 45,1 %;
100 % = 1; 2 = 200 %.
Слайд 9 Чтобы выразить в процентах часть величины, заданную обыкновенной
дробью, нужно сначала эту дробь обратить в десятичную.
3/8 =
0,375, т. е. 3/8 – это 37,5 %
Слайд 10
Запомни!
Например, 17 % от 500 кг означает 17 частей
по 5 кг каждая, то есть 85 кг. Справедливо
также утверждение, что 200 % от 500 кг является 1000 кг. Поскольку по отношению к половине тонны, тонна соответствует 2×100 %.Слайд 11 В 1685 году в Париже была издана книга
«Руководство по коммерческой арифметике» Матье де ла Порта.
В
одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento). Однако наборщик принял это «cto» за дробь и напечатал «%». Так из-за опечатки этот знак вошёл в обиход.Pro cento – cento – cto - c/o - %
Как возник знак процента
Изобретение математических знаков и символов значительно облегчило изучение математики и способствовало дальнейшему ее развитию.
Происхождение обозначения.
Слайд 12 В тексте знак процента используется только при числах
в цифровой форме, от которых при наборе отделяется неразрывным
пробелом (доход 67 %), кроме случаев, когда знак процента используется для сокращённой записи сложных слов, образованных при помощи числительного и прилагательного процентный. Например: 20%-я сметана (означает двадцатипроцентная сметана), 10%-й раствор, 20%-му раствору, но жирность сметаны составляет 20 %, раствор концентрацией 10 % и т. п.Это правило набора введено в действие в 1982 году нормативным документом ГОСТ 8.417—81 (впоследствии заменённым на ГОСТ 8.417—2002); ранее нормой было не отделять знак процента пробелом от предшествующей цифры.В настоящее время правило отбивки знака процента не является общепризнанным. До сих пор многие российские издательства не следуют рекомендациям ГОСТ 8.417—2002 и по-прежнему придерживаются традиционных правил набора, то есть при наборе знак процента от предшествующего числа не отделяется,
что было мною замечено в школьных учебниках при подготовке данной презентации.
Правила набора.
Слайд 13 Ударение в слове процент в единственном и множественном
числе во всех падежах сохраняется на втором слоге.
Например:
сто один процент; не более восемнадцати процентов.а) Сочетание «несколько процентов (от чего?) …» используется, если зависимое слово – числительное.
Например, «десять процентов от шестидесяти».
б) Сочетание «несколько процентов (чего?) …» используется, если зависимое слово – существительное, не имеющее количественного значения.
Например, «тридцать процентов населения».
Слайд 14 в) Если зависимое слово по смыслу связано с
количеством, допустимы обе конструкции.
Например, «шесть процентов зарплаты» и «шесть
процентов от зарплаты».Слова «процент», «проценты» читаются в большинстве случаев в том же падеже, что и числительное.
Например:
1/5 = 20 % - одна пятая равна двадцати (д. п.) процентам (д. п.)
0,6 > 50 % - ноль целых шесть десятых больше пятидесяти (р. п.) процентов (р. п.).
После любого падежа числительных, оканчивающихся словом «тысяча» или «миллион», слово «проценты» ставится в родительном падеже. Например, «прирост производительности труда равен тысяче (д. п.) процентов (д. п.)».
Слайд 15 Иногда применяют и более мелкие доли целого –
тысячные, то есть десятые части процента. Их называют «промилле»
происходит от лат. «pro mille», что означает в переводе «с тысячи» или «тысячная доля» — 1/10 процента. Обозначается дробью «0 делить на 00» (‰). Как и «процент», тоже используется для обозначения доли чего-либо по отношению к целому.Соотношение к процентам и десятичным дробям
Знакомьтесь родственник процента – промилле.
Слайд 16 Величина в промилле от массы, выраженной в килограммах,
эквивалентна массе в граммах. От массы в тоннах — килограммам.
Например,
фраза «солёность воды составляет 11 ‰ (одиннадцать промилле)», это то- же самое, что и 1,1 % и означает, что из общей массы воды 0,011 (11 тысячных) занимают соли; так, если взять 1 кг воды, то в ней будет 0,011×1000 = 11 г солей.Слайд 17 Поскольку проценты выражаются дробями, то задачи на проценты,
по существу, являются теми же задачами на дроби.
Какое количество
В составляет Р % от А? Нахождение указанного процента от заданного числа. Формула: А∙(Р/100)
Чтобы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь.
Пример. Швейная фабрика выпустила 1200 костюмов. Из них 30% - костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?
В = 1200∙30/100 = 1200∙0,3 = 360
Виды задач на проценты с примерами.
Слайд 18 Какого количество В, Р % от которого есть
А? Нахождение числа по заданному другому числу и его
величине в процентах от искомого числа. Формула: А∙(100/Р)Пример. За тест по математике отметку «5» получили 12 учеников, что составляет 30% всех учеников. Сколько учеников выполняло тест?
В = 100∙12/30 = 40
Слайд 19 Какого количество В, большее (меньшее) чем А, на
Р%? Увеличение (уменьшение) числа на заданный процент. Формула: A+A∙P/100 =
А∙(1+Р/100), A-A∙P/100 = А∙(1-Р/100)Пример. Рабочий изготовил 720 деталей за смену, перевыполнив план на 20 %. Сколько деталей составляет плановое задание рабочего?
А∙(1+20/100) =720
В = 720/(1+20/100) = 720/(1+1/5) = 720/1,2 = 600
Пример. Денежная сумма к выдаче за минусом подоходного налога (13 процентов). Пусть оклад составляет 10 000 рублей. Тогда сумма к выдаче составляет:
В= 10000 * (1 - 13 / 100) = 10000 * 0.87 = 8700.
Слайд 20 Сколько % составляет А от В? Нахождение процентного
выражения одного числа от другого.
Формула: (А/В)∙100%
Чтобы найти, сколько
процентов одно число составляет от другого, нужно разделить первое число на второе и полученную дробь записать в виде процентов.
Пример. Завод произвёл за год 40000 автомобилей, а в следующем году – только 36000 автомобилей. Сколько процентов это составило по отношению к выпуску предыдущего года?
P = 36000 : 40000 · 100 = 90% .
Слайд 21 На сколько % А больше (меньше), чем В? Формула:
(А-В)/В∙100%, (В-А)/В∙100%
Пример. Число учащихся, записавшихся в данную школу, выросло
с 351 до 396 человек. На сколько процентов возросло это число? Прирост составил 396 – 351 = 45 человек. Записывая дробь 45/351 в процентах, получаем:
45/351 = 0,128 = 12,8%.
Слайд 22 Задача 1. В январе стоимость билета в цирк
была 200 рублей. В феврале его стоимость подорожала на
15%, а в марте – ещё на 20%. Какая стала стоимость билета в цирк в марте.Немного житейских задач.
Слайд 23
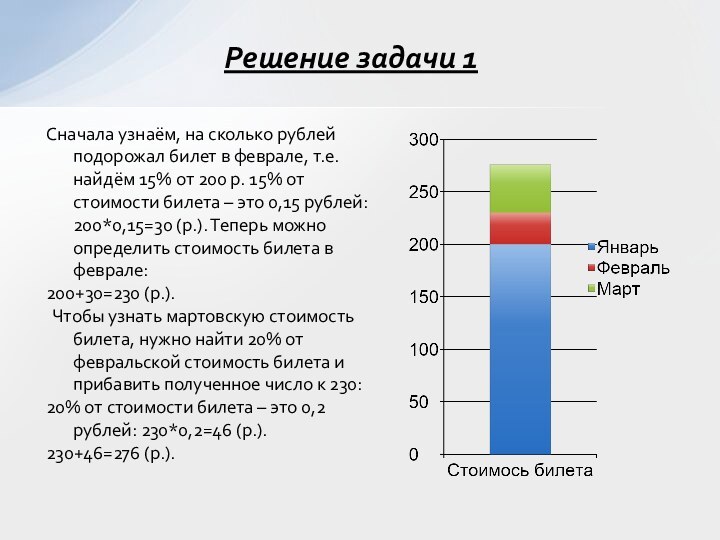
Cначала узнаём, на сколько рублей подорожал билет в
феврале, т.е. найдём 15% от 200 р. 15% от
стоимости билета – это 0,15 рублей: 200*0,15=30 (р.). Теперь можно определить стоимость билета в феврале:200+30=230 (р.).
Чтобы узнать мартовскую стоимость билета, нужно найти 20% от февральской стоимость билета и прибавить полученное число к 230:
20% от стоимости билета – это 0,2 рублей: 230*0,2=46 (р.).
230+46=276 (р.).
Решение задачи 1
Слайд 24
Задача 2. За хорошую учебу своего сына мама
с папой решили купить ему новый компьютер. Первоначальная стоимость
компьютера составляла 20 000 руб. Семье повезло дважды: воскресная скидка 5 % и новогоднее предложение – скидка 10 %. Определите цену товара после двух понижений: сначала на 5 %, а потом на 10 %.Слайд 25 20 000•5/100 = 1000 руб. – составляют 5
%;
20 000 – 1000 = 19 000 руб. –
цена после первой скидки; 19 000/10 = 1900 руб. – составляют 10 %
19 000 – 1900 = 17 100 руб. – цена товара после двух понижений.
Решение задачи 2
Слайд 26 Задача 3. Собрали 100 кг грибов. Оказалось, что
их влажность 99%. Когда грибы подсушили, влажность снизилась до
98%.Какой стала масса грибов после подсушивания?
Слайд 27 По условию в 100 кг грибов содержится 1
кг сухого вещества (100 - 0,99 100 = 1).
Так как масса сухого вещества в общей массе грибов постоянна (1 кг) и стала после подсушивания составлять 2% (100 - 98 = 2), то масса грибов после подсушивания стала равной 50 кг (если 2% - 1 кг, то 100% - 50 кг).Масса грибов после подсушивания стала 50 кг.
Решение задачи 3
Слайд 28 Напоследок мне хочется рассмотреть заинтересовавшие меня проценты, применяемые
в экономике о которых настойчиво сообщают нам все средства
массовой информации. Для этого они были придуманы много лет тому назад – это проценты в сфере бизнеса.
Слайд 29
Если проценты на депозит начисляются один раз в
конце срока депозита, то сумма процентов вычисляется по формуле
простых процентов.S = K + (K*P*d/D)/100 Sp = (K*P*d/D)/100
Где: S — сумма банковского депозита с процентами, Sp — сумма процентов (доход), K — первоначальная сумма (капитал), P — годовая процентная ставка, d — количество дней начисления процентов по привлеченному вкладу, D — количество дней в календарном году (365 или 366).
Расчет процентов на банковский депозит. Формула расчета простых процентов.
Слайд 30
Пример 1. Банком принят депозит в сумме 100
тыс. рублей сроком на 1 год по ставке 20
процентов.S = 100000 + 100000*20*365/365/100 = 120000 Sp = 100000 * 20*365/365/100 = 20000
Пример 2. Банком принят депозит в сумме 100 тыс. рублей сроком на 30 дней по ставке 20 процентов.
S = 100000 + 100000*20*30/365/100 = 101643.84 Sp = 100000 * 20*30/365/100 = 1643.84
Слайд 31 Если проценты на депозит начисляются несколько раз через
равные промежутки времени и зачисляются во вклад, то сумма
вклада с процентами вычисляется по формуле сложных процентов.S = K * (1 + P*d/D/100)N
Где: S — сумма депозита с процентами, К — сумма депозита (капитал), P — годовая процентная ставка, N — число периодов начисления процентов.
При расчете сложных процентов проще вычислить общую сумму с процентами, а потом вычислить сумму процентов (доход):
Sp = S - K = K * ( 1 + P*d/D/100 )N - K
или
Sp = K * ((1 + P*d/D/100)N - 1)
Расчет процентов на банковский депозит при начислении процента на процент. Формула расчета сложных процентов.
Слайд 32 Пример 1. Принят депозит в сумме 100 тыс.
рублей сроком на 90 дней по ставке 20 процентов
годовых с начислением процентов каждые 30 дней.S = 100000 * (1 + 20*30/365/100)3 = 105 013.02 Sp = 100000 * ((1 + 20*30/365/100)N - 1) = 5 013.02
Пример 2. Проверим формулу начисления сложных процентов для случая из предыдущего примера.
Разобьем срок депозита на 3 периода и рассчитаем начисление процентов для каждого периода, использую формулу простых процентов.
S1 = 100000 + 100000*20*30/365/100 = 101643.84 Sp1 = 100000 * 20*30/365/100 = 1643.84 S2 = 101643.84 + 101643.84*20*30/365/100 = 103314.70 Sp2 = 101643.84 * 20*30/365/100 = 1670.86 S3 = 103314.70 + 103314.70*20*30/365/100 = 105013.02 Sp3 = 103314.70 * 20*30/365/100 = 1698.32
Общая сумма процентов с учетом начисления процентов на проценты (сложные проценты)
Sp = Sp1 + Sp2 + Sp3 = 5013.02
Таким образом, формула вычисления сложных процентов верна.
Примеры к Расчету процентов на банковский депозит при начислении процента на процент. Формула расчета сложных процентов.
Слайд 33
Я повторил пройдённый материал по процентам.
Познакомился с
заинтересовавшими меня процентами в банковской сфере.
Узнал, что сейчас
область применения процентов очень велика по сравнению со временем их рождения, когда их применяли только ростовщики. Я понял, что проценты можно применять везде. И поэтому «Проценты вокруг нас» существуют и уже никуда не денутся.
Знание и понимание процентов необходимо в современной жизни.
Заключение.





























