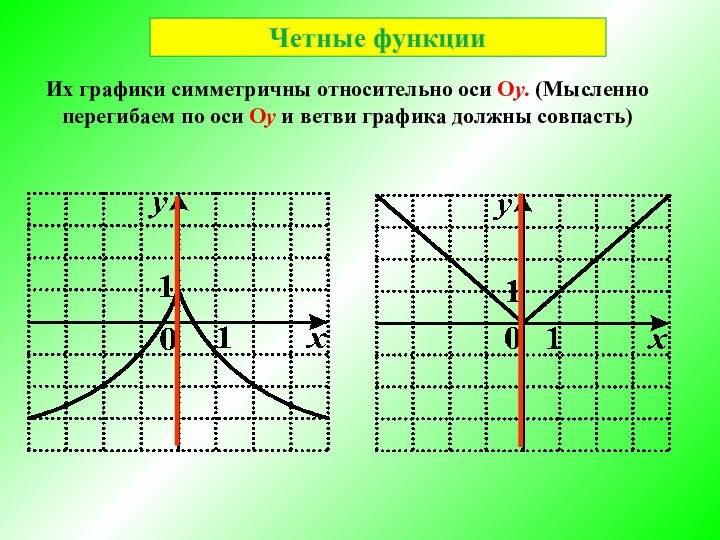
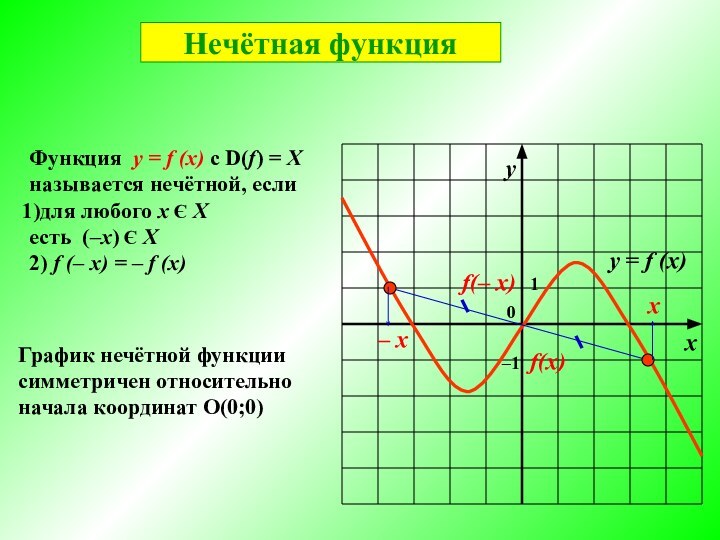
f (x) с D(f) = X называется чётной, если
для любого x Є X
есть (‒х) Є X
2) f (‒ x) = f (x)
Чётная функция
х
‒ х
f(х)
f(‒ х)
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


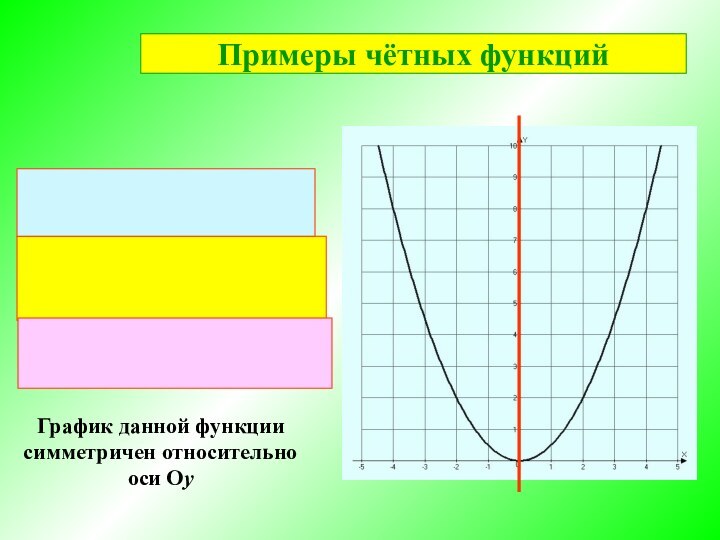
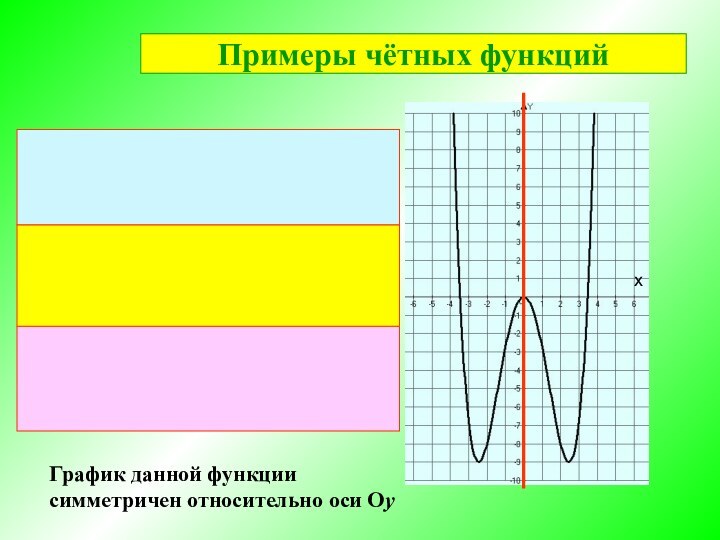
Чётная функция
х
‒ х
f(х)
f(‒ х)
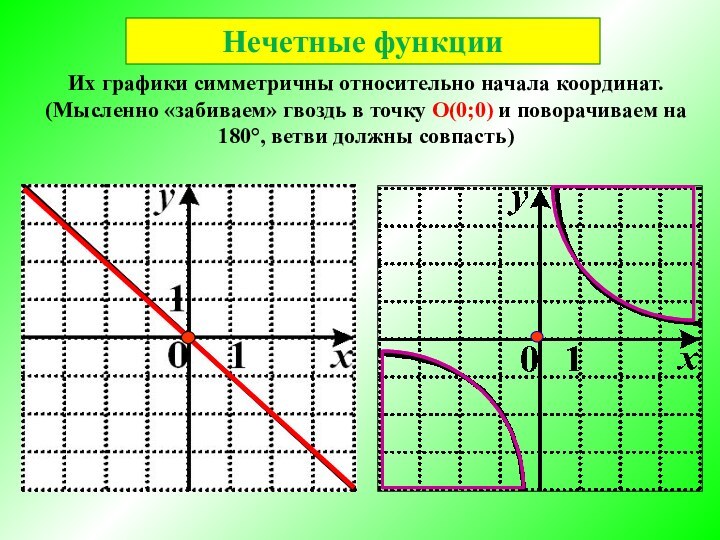
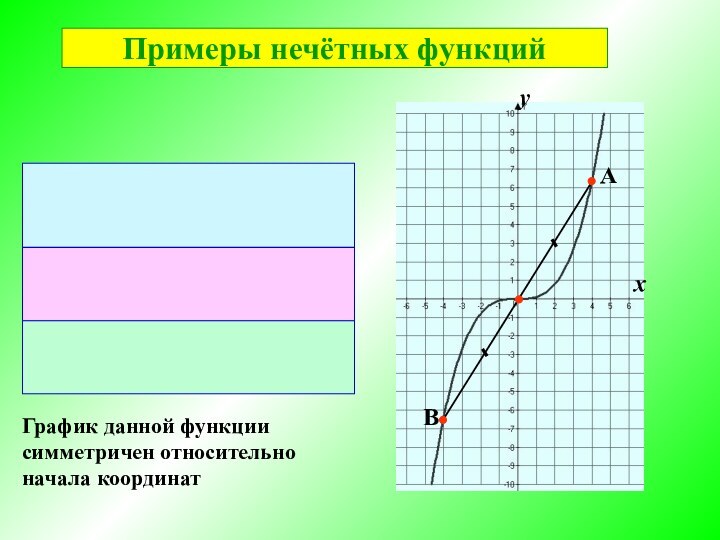
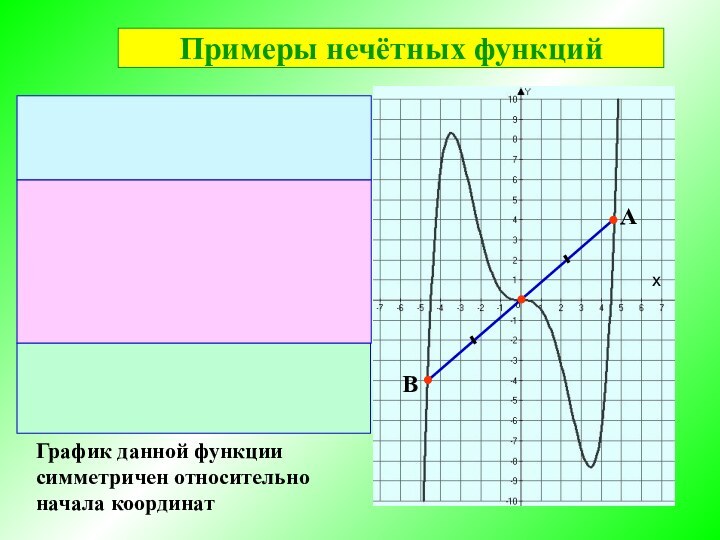
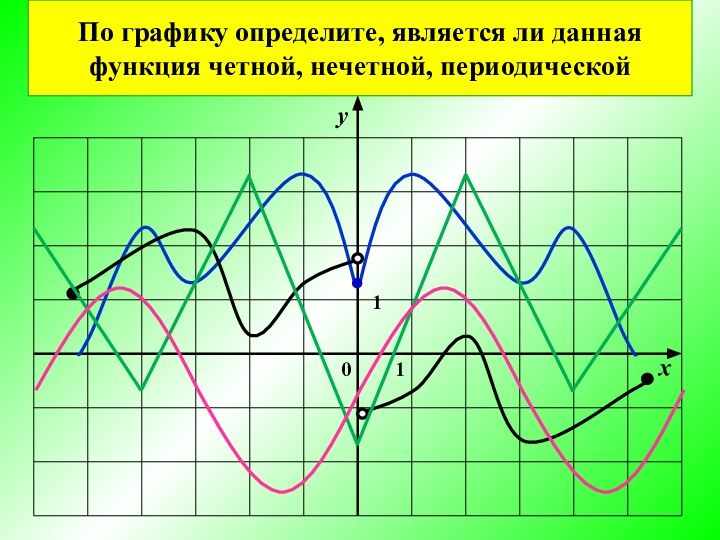
Нечётная функция
х
‒ х
f(‒ х)
f(х)
у = f (x)
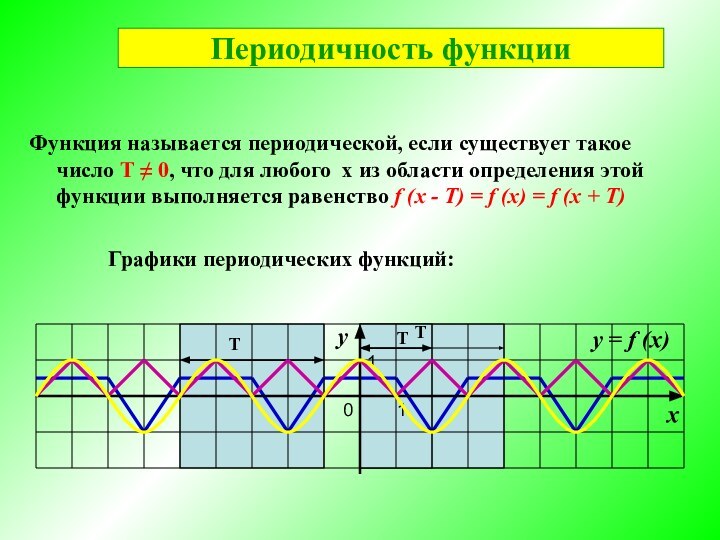
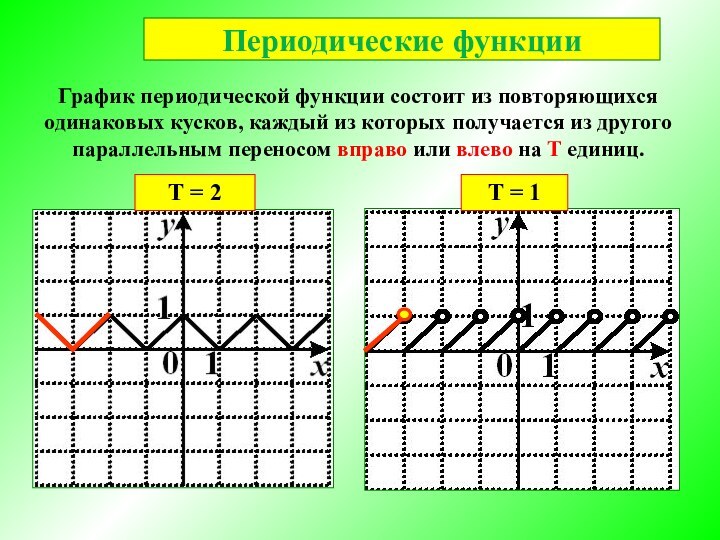
Графики периодических функций:
Т
T
T
Периодичность функции
Т = 2
Т = 1