Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

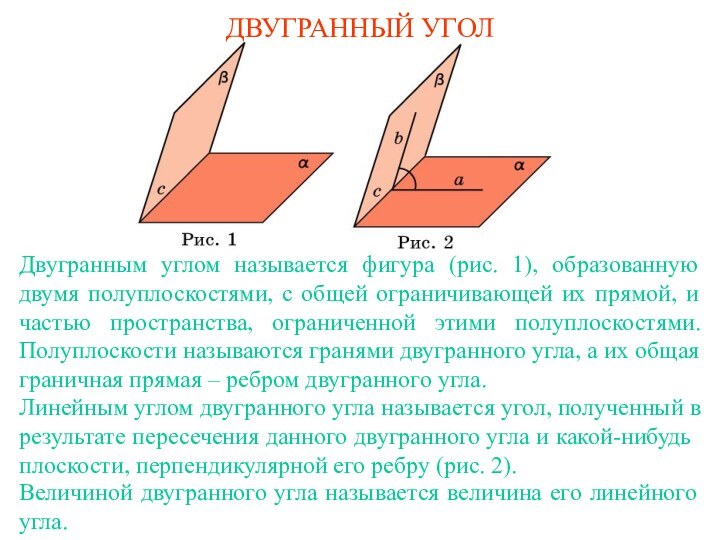
Презентация на тему Двугранный угол

Содержание

2. Упражнение 1Какой угол образует ребро двугранного угла
3. Упражнение 2Плоскости двух равнобедренных треугольников с общим
4. Упражнение 3Треугольник MAB и квадрат ABCD заданы
5. Упражнение 4В правильной треугольной призме найдите угол между боковыми гранями.Ответ: 60о.
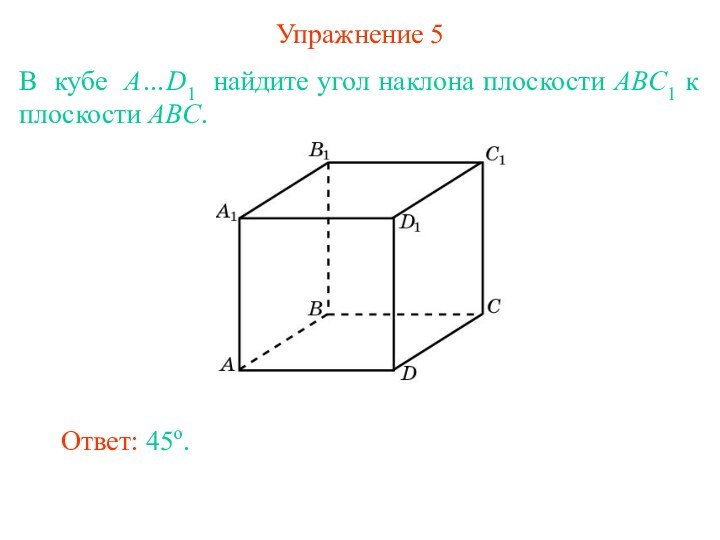
6. Упражнение 5В кубе A…D1 найдите угол наклона плоскости ABC1 к плоскости ABC.Ответ: 45о.
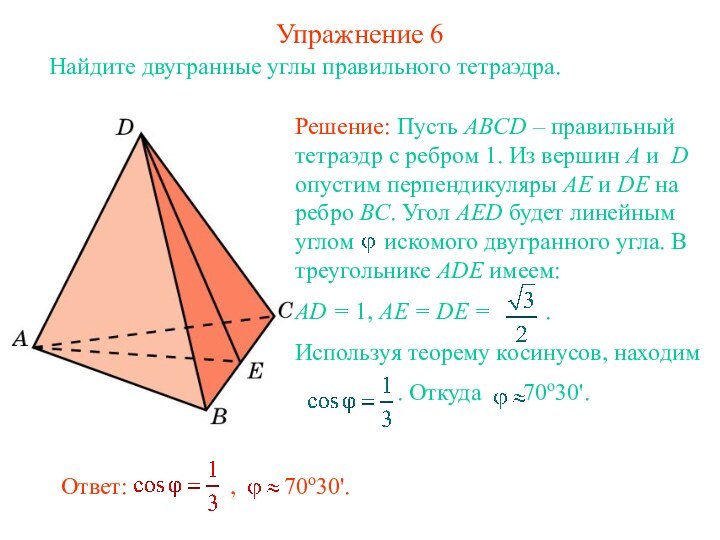
7. Упражнение 6Найдите двугранные углы правильного тетраэдра.
8. Упражнение 7Найдите геометрическое место точек в пространстве,
9. Упражнение 8Через сторону BC треугольника ABC проведена
10. Упражнение 9Через катет BC=a равнобедренного прямоугольного треугольника
11. Упражнение 10Через сторону BC треугольника ABC проведена
12. Упражнение 11Дан квадрат ABCD, через вершину D
13. Упражнение 12Основанием высоты четырехугольной пирамиды является точка
14. Упражнение 13В основании прямой призмы параллелограмм со
15. Упражнение 14Боковое ребро прямой призмы равно 6
16. Упражнение 15Сторона основания правильной треугольной призмы равна
17. Упражнение 16Ребро куба равно a. Найдите площадь
18. Упражнение 17Через середины двух смежных сторон основания
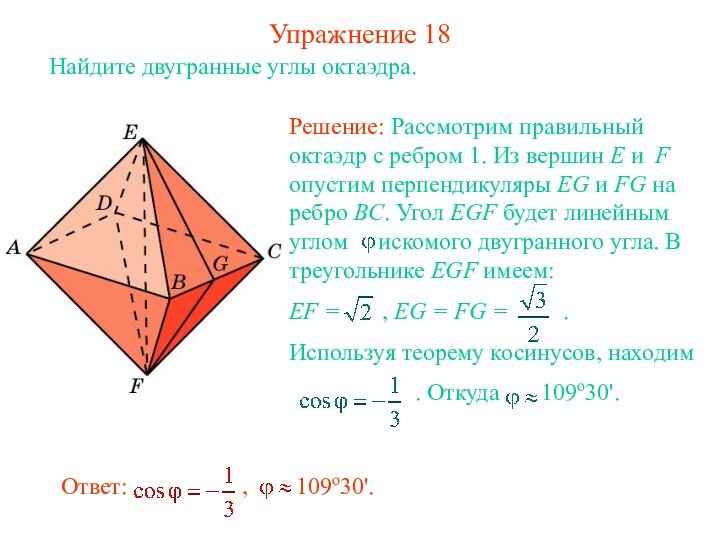
19. Упражнение 18Найдите двугранные углы октаэдра.
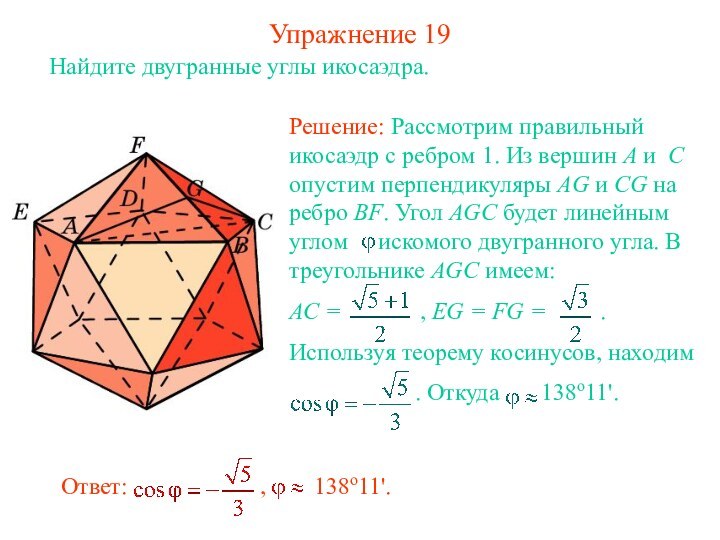
20. Упражнение 19Найдите двугранные углы икосаэдра.
21. Скачать презентацию
22. Похожие презентации

Упражнение 1Какой угол образует ребро двугранного угла с любой прямой, лежащей в плоскости его линейного угла?Ответ: 90о.

ДВУГРАННЫЙ УГОЛДвугранным углом называется фигура (рис. 1), образованную двумя полуплоскостями, с общей

Упражнение 2Плоскости двух равнобедренных треугольников с общим основанием образуют двугранный угол. Верно

Упражнение 3Треугольник MAB и квадрат ABCD заданы таким образом, что MB -

Упражнение 4В правильной треугольной призме найдите угол между боковыми гранями.Ответ: 60о.

Упражнение 5В кубе A…D1 найдите угол наклона плоскости ABC1 к плоскости ABC.Ответ: 45о.

Упражнение 6Найдите двугранные углы правильного тетраэдра.

Упражнение 7Найдите геометрическое место точек в пространстве, равноудаленных от двух пересекающихся плоскостей.

Упражнение 8Через сторону BC треугольника ABC проведена плоскость  под углом 30°

Упражнение 9Через катет BC=a равнобедренного прямоугольного треугольника ABC (угол C равен 90°)

Упражнение 10Через сторону BC треугольника ABC проведена плоскость под углом 30° к

Упражнение 11Дан квадрат ABCD, через вершину D параллельно диагонали AC проведена плоскость

Упражнение 12Основанием высоты четырехугольной пирамиды является точка пересечения диагоналей основания пирамиды. Верно

Упражнение 13В основании прямой призмы параллелограмм со сторонами 4 дм и 5

Упражнение 14Боковое ребро прямой призмы равно 6 см. Ее основание – прямоугольный

Упражнение 15Сторона основания правильной треугольной призмы равна 4 см. Найдите площадь сечения

Упражнение 16Ребро куба равно a. Найдите площадь сечения куба плоскостью, проходящей через

Упражнение 17Через середины двух смежных сторон основания правильной четырехугольной призмы проведена плоскость,

Упражнение 18Найдите двугранные углы октаэдра.

Упражнение 19Найдите двугранные углы икосаэдра.

Упражнение 20Найдите двугранные углы додекаэдра.

Слайды презентации

Слайд 2 Упражнение 1
Какой угол образует ребро двугранного угла с

Упражнение 1Какой угол образует ребро двугранного угла с любой прямой, лежащей

любой прямой, лежащей в плоскости его линейного угла?
Ответ: 90о.

Слайд 3 Упражнение 2
Плоскости двух равнобедренных треугольников с общим основанием

Упражнение 2Плоскости двух равнобедренных треугольников с общим основанием образуют двугранный угол.

образуют двугранный угол. Верно ли утверждение о том, что

высоты, проведенные к общему основанию треугольников, образуют линейный угол двугранного угла?

Ответ: Да.

Слайд 4 Упражнение 3
Треугольник MAB и квадрат ABCD заданы таким

образом, что MB - перпендикуляр к плоскости квадрата. Какой

угол можно считать углом между плоскостями AMD и ABC?

Ответ: MBC.

Слайд 5 Упражнение 4
В правильной треугольной призме найдите угол между

боковыми гранями.
Ответ: 60о.

Слайд 6 Упражнение 5
В кубе A…D1 найдите угол наклона плоскости

ABC1 к плоскости ABC.
Ответ: 45о.

Слайд 7 Упражнение 6
Найдите двугранные углы правильного тетраэдра.

Слайд 8 Упражнение 7
Найдите геометрическое место точек в пространстве, равноудаленных

Упражнение 7Найдите геометрическое место точек в пространстве, равноудаленных от двух пересекающихся

от двух пересекающихся плоскостей.
Ответ: Две биссектральные плоскости.

Слайд 9 Упражнение 8
Через сторону BC треугольника ABC проведена плоскость

Упражнение 8Через сторону BC треугольника ABC проведена плоскость  под углом

 под углом 30° к плоскости треугольника. Высота AD

треугольника ABC равна a. Найдите расстояние от вершины A треугольника до плоскости α.

Слайд 10 Упражнение 9
Через катет BC=a равнобедренного прямоугольного треугольника ABC

Упражнение 9Через катет BC=a равнобедренного прямоугольного треугольника ABC (угол C равен

(угол C равен 90°) проведена плоскость α, образующая с

плоскостью треугольника угол 30°. Найдите расстояние от вершины A до плоскости α.

Слайд 11 Упражнение 10
Через сторону BC треугольника ABC проведена плоскость

Упражнение 10Через сторону BC треугольника ABC проведена плоскость под углом 30°

под углом 30° к плоскости треугольника; угол C равен

150°, AC = 6. Найдите расстояние от вершины A до этой плоскости.

Ответ: 1,5.

Слайд 12 Упражнение 11
Дан квадрат ABCD, через вершину D параллельно

Упражнение 11Дан квадрат ABCD, через вершину D параллельно диагонали AC проведена

диагонали AC проведена плоскость α, образующая с диагональю BD

угол 60°. Чему равен угол между плоскостью квадрата и плоскостью α?

Ответ: 60о.

Слайд 13 Упражнение 12
Основанием высоты четырехугольной пирамиды является точка пересечения

Упражнение 12Основанием высоты четырехугольной пирамиды является точка пересечения диагоналей основания пирамиды.

диагоналей основания пирамиды. Верно ли, что двугранные углы, образованные

боковыми гранями пирамиды с плоскостью основания, равны, если основанием пирамиды является: а) квадрат; б) параллелограмм; в) ромб; г) равнобедренная трапеция?

Ответ: а) Да;

б) нет;

в) да;

г) нет.

Слайд 14 Упражнение 13
В основании прямой призмы параллелограмм со сторонами

Упражнение 13В основании прямой призмы параллелограмм со сторонами 4 дм и

4 дм и 5 дм. Угол между ними 30°.

Найдите площадь сечения призмы плоскостью, если известно, что она пересекает все боковые ребра и образует с плоскостью основания угол 45°.

Слайд 15 Упражнение 14
Боковое ребро прямой призмы равно 6 см.

Упражнение 14Боковое ребро прямой призмы равно 6 см. Ее основание –

Ее основание – прямоугольный треугольник с катетами 3 см

и 2 см. Найдите площади сечений призмы плоскостями, проходящими через каждый из данных катетов и образующими углы 60° с плоскостью основания.

Ответ: 6 см2.

Слайд 16 Упражнение 15
Сторона основания правильной треугольной призмы равна 4

Упражнение 15Сторона основания правильной треугольной призмы равна 4 см. Найдите площадь

см. Найдите площадь сечения призмы плоскостью, проходящей через середины

двух сторон основания и образующей угол 45° с его плоскостью, если известно, что плоскость пересекает: а) только одно боковое ребро призмы; б) два ее боковых ребра.