- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Плащадь трапеции
Содержание
- 2. Актуализация знаний учащихся.Дать определение трапеции. Виды
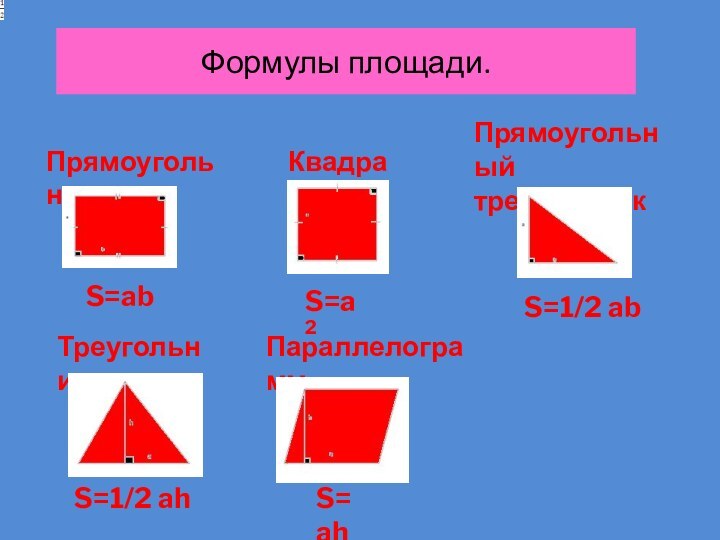
- 3. Формулы площади.ПрямоугольникКвадратПрямоугольный треугольникТреугольникПараллелограммS=ab S=a2S=ab S=ab S=S=S=S=S=S=S=1/2 ab S=1/2 ahS= ah
- 4. Уровень А 1)
- 6. Уровень Б 2. Дано: ABCD-равнобедр. трапеция;
- 7. Уровень В.Дано: ABCD-равнобедр. трапеция;
- 8. Уровень В 2.Дано: ABCD-равнобедр.трапеция; АС перпенд. BD; BC+AD=18cмНайти: Sтрап. Решение:Пусть BC=х,тогда AD=18-хТреугольник BOC-прямоуг., равнобедр.Значит
- 9. Различные способы доказательства теоремы
- 10. Различные способы доказательства теоремы о площади трапеции
- 11. Высота больше меньшего основания на 6 см,
- 12. В трапеции ABCD BC и AD –
- 13. «Трапеция»- слово греческое, означавшее в древности «столик»
- 14. Скачать презентацию
- 15. Похожие презентации
Актуализация знаний учащихся.Дать определение трапеции. Виды трапеций:равнобедренная трапецияпрямоугольная трапецияТрапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.








Слайд 2
Актуализация знаний учащихся.
Дать определение трапеции.
Виды трапеций:
равнобедренная
трапеция
а две другие стороны не параллельны.
Слайд 3
Формулы площади.
Прямоугольник
Квадрат
Прямоугольный
треугольник
Треугольник
Параллелограмм
S=ab
S=a2
S=
ab
S=
ab
S=
S=
S=
S=
S=
S=
S=1/2 ab
S=1/2
ah
S= ah
Слайд 4 Уровень А 1) 4см
и 10см
2) 24см2 Уровень Б 1) 5см; 15см; 25см;
2) 32см2
Уровень В 1) 22см2
2) 81см2
Слайд 5
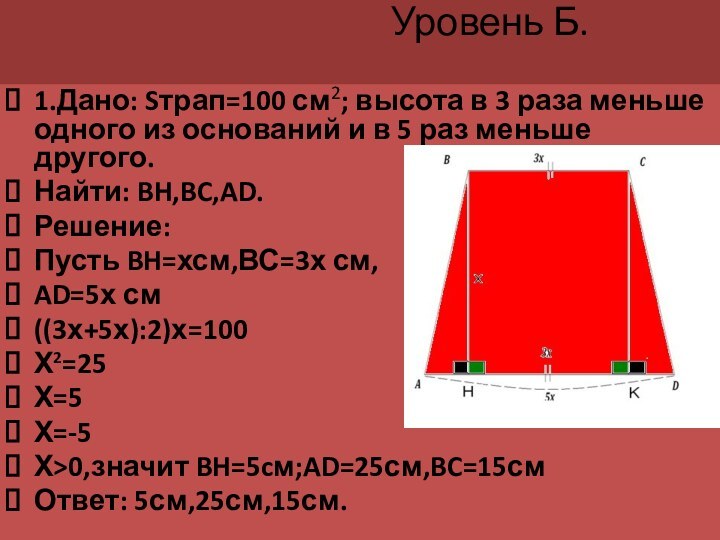
Уровень Б.
1.Дано:
Sтрап=100 см2; высота в 3 раза меньше одного из оснований и в 5 раз меньше другого.Найти: BH,BC,AD.
Решение:
Пусть BH=хсм,ВС=3х см,
AD=5х см
((3х+5х):2)х=100
Х2=25
Х=5
Х=-5
Х>0,значит BH=5cм;AD=25см,BC=15см
Ответ: 5см,25см,15см.
Слайд 6
Уровень Б
2.
Дано: ABCD-равнобедр.
трапеция;
перпендикулярно AD,CKперпендикулярно AD.
Пусть ВС=BH=х,тогда HK=AH=KD=х,
(треугольник ABH-прямоугольный,
равнобедренный),значит
3х=12; Х=4
Sтрап=((4+12):2)4
Sтрап=32см2
Ответ:32см2.
Слайд 7
Уровень В.
Дано: ABCD-равнобедр. трапеция;
Решение:
AB+CD=30-22=8см
AB=CD=4см
Д.п. BH перпендикулярно AD,
CK перпендикулярно AD
Треугольник ABH-прямоугольный
BH=АВ:2=2см
(по св-ву прямоугольного
треугольника)Sтрап=(22:2)2=22см2
Ответ:22см2
Слайд 8
Уровень В
2.
Дано: ABCD-равнобедр.трапеция; АС перпенд. BD; BC+AD=18cм
Найти: Sтрап.
Решение:
Пусть BC=х,тогда AD=18-х
Треугольник BOC-прямоуг., равнобедр.
Значит
BH=HO=х:2Треугольник AOK-прямоугольный,р/б,значит AК=KO=(18-х):2
HK=HO+KO=9см
Sтрап.=9*9;Sтрап.=81см2
Ответ:81см2
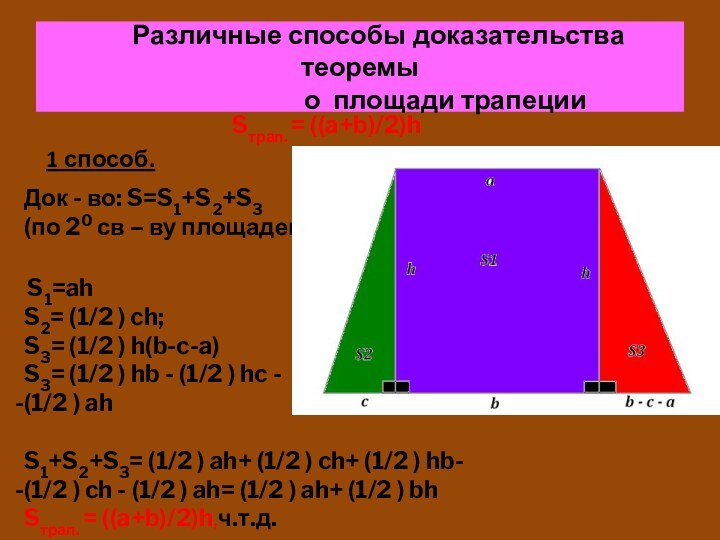
Слайд 9 Различные способы доказательства теоремы
о площади трапеции
1 способ.
Док - во: S=S1+S2+S3
(по 20 св – ву площадей)
S1=ah
S2= (1/2 ) ch;
S3= (1/2 ) h(b-c-a)
S3= (1/2 ) hb - (1/2 ) hc -
(1/2 ) ah
S1+S2+S3= (1/2 ) ah+ (1/2 ) ch+ (1/2 ) hb-
(1/2 ) ch - (1/2 ) ah= (1/2 ) ah+ (1/2 ) bh Sтрап. = ((a+b)/2)h,ч.т.д.
Sтрап. = ((a+b)/2)h
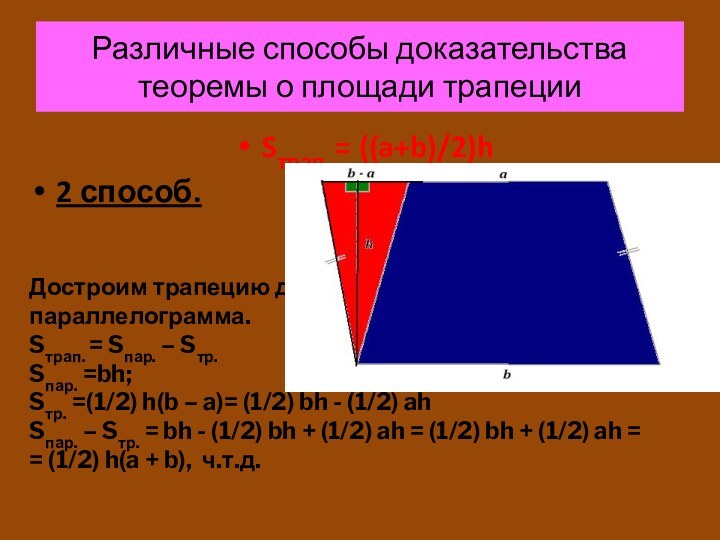
Слайд 10 Различные способы доказательства теоремы о площади трапеции
Sтрап. = ((a+b)/2)h
2 способ.
Достроим трапецию до
параллелограмма.
Sтрап. = Sпар. – Sтр.
Sпар. =bh;
Sтр. =(1/2) h(b – a)= (1/2) bh - (1/2) ah
Sпар. – Sтр. = bh - (1/2) bh + (1/2) ah = (1/2) bh + (1/2) ah =
= (1/2) h(a + b), ч.т.д.
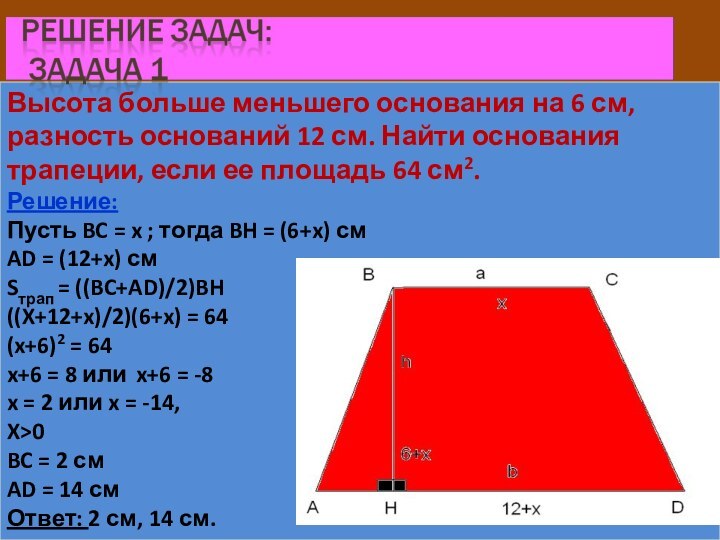
Слайд 11 Высота больше меньшего основания на 6 см, разность
оснований 12 см. Найти основания трапеции, если ее площадь
64 см2.Решение:
Пусть BC = x ; тогда BH = (6+x) см
AD = (12+x) см
Sтрап = ((BC+AD)/2)BH
((X+12+x)/2)(6+x) = 64
(x+6)2 = 64
x+6 = 8 или x+6 = -8
x = 2 или x = -14,
X>0
BC = 2 см
AD = 14 см
Ответ: 2 см, 14 см.
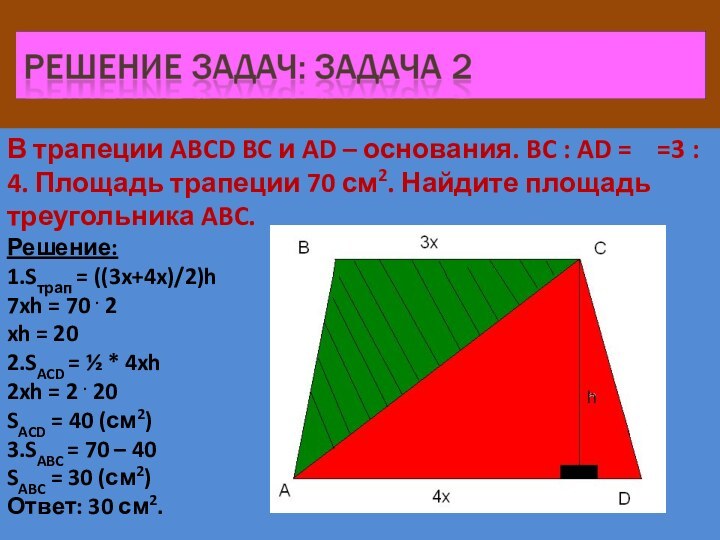
Слайд 12 В трапеции ABCD BC и AD – основания.
BC : AD = =3 : 4. Площадь
трапеции 70 см2. Найдите площадь треугольника ABC.Решение:
1.Sтрап = ((3x+4x)/2)h
7xh = 70 . 2
xh = 20
2.SACD = ½ * 4xh
2xh = 2 . 20
SACD = 40 (см2)
3.SABC = 70 – 40
SABC = 30 (см2)
Ответ: 30 см2.
Слайд 13 «Трапеция»- слово греческое, означавшее в древности «столик» (по-гречески,
«трапедзион» -столик, обеденный стол)
В начале термин «трапеция»
применяется не в современном , в другом смысле - любой четырехугольник. Трапеция в нашем смысле встречается впервые у древнегреческого математика Пасидона. В средние века трапецией называли, по Евклиду, любой четырехугольник (кроме трапеции) лишь в 18 веке слово приобретает современный смысл.интересные факты
история трапеции:
,