- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Формула суммы и первых членов геометрической профессии
Содержание
- 2. Формула суммы n первых членов геометрической прогрессии.
- 3. Цели урока: повторить определение геометрической прогрессии;повторить формулу
- 4. Оборудование урока:интерактивный комплекс;дидактические карточки
- 5. Тип урока:урок-соревнование с использованием элементов дидактической игры.
- 6. План проведения урокаповторение ранее изученного материала;подведение первого
- 7. Задания для команд.Правильно ли дано определение геометрической прогрессии?
- 8. Числовая последовательность (отличных от нуля членов), каждый
- 9. Правильный ответГеометрической последовательностью называется последовательность отличных от
- 10. Является ли геометрической прогрессией числовая последовательность ?
- 11. Для 1-ой команды4, 16, 64,…Для 2-ой команды1, 3, 9, 27,…
- 12. Для 1-ой команды6, 6, 6, 6,…..Для 2-ой команды16, 16, 16, 16,…..
- 13. Для 1-ой команды-2, 4, -8, 12,…Для 2-ой команды-4, -2. -1, 1, 2,…
- 14. Какая из формул задает геометрическую прогрессию?
- 15. Для 1-ой командыХn =2nДля 2-ой командыXn=3n
- 16. Для 1-ой командыBn=2n+1Для 2-ой командыBn=3n-1
- 17. Для 1-ой командыZn=4х5nДля 2-ой командыZn=-3х2n
- 18. Задача Однажды незнакомец постучал в окно к
- 19. Ответьте на вопрос:Кто остался в выигрыше?
- 20. Решение задачи1-ый день 1коп.2-ой
- 21. Что получится за последовательность?
- 22. В1=1, q=2Получим геометрическую прогрессиюВ30=1·2^29=2^10·2^10·2^9=
- 23. В30=1024 ·1024 · 512= 1036870912 коп.
- 24. Сколько денег получал купец?
- 25. 100000·30=3.000.000рублей
- 26. А сколько он должен был отдать?
- 27. Для этого нужно сложить все отданные деньги, а затем из 3000000 вычесть полученную сумму.
- 28. Как вы думаете есть ли какое-нибудь правило, которое позволит облегчить это вычисление?
- 29. Для этого достаточно иметь формулу для вычисления суммы n первых членов геометрической прогрессии.
- 30. Sn = b1+b2+b3+……+bn * (g) (1)
- 31. Sn*g=b2+b3+b4+…..=bn-1+bn*g (2) Вычтем почленно из равенства (2) равенство (1)
- 32. Sn*g- Sn= (b2-b1)+(b3-b2)+….+ +(bn-bn-1)+ bn*g=bn*g-b1
- 33. Sn (g-1) = bn*g-b1 =b1*g^(n-1)*g-b1== b1 (g^n-1)Sn=
- 34. Давайте найдем ответ для нашей задачи
- 35. S30 =1*(2^30-1) =1073731824коп.==10.734.418руб.24коп.
- 36. Так кто же выиграл от этой сделки?10.734.418руб.24коп.-3.000000руб.==7. 737.418руб.24коп.
- 37. НЕЗНАКОМЕЦ.
- 38. Скачать презентацию
- 39. Похожие презентации
Формула суммы n первых членов геометрической прогрессии.
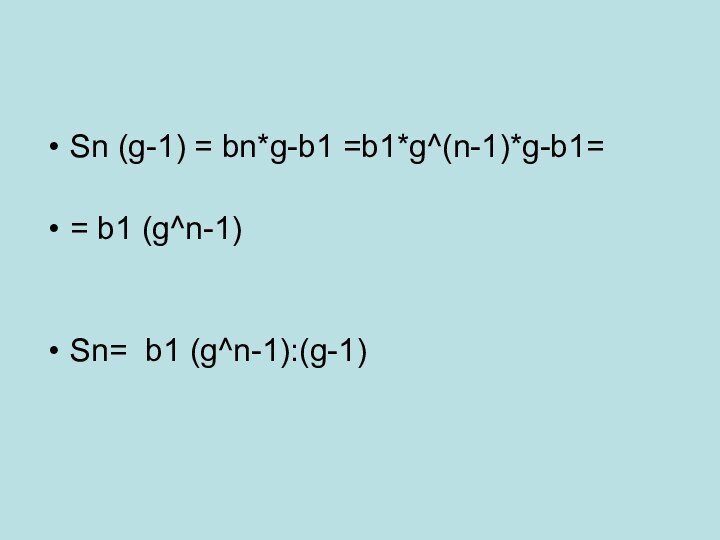
Слайд 3
Цели урока:
повторить определение геометрической прогрессии;
повторить формулу n-ого
члена геометрической прогрессии;
Sn.
Слайд 6
План проведения урока
повторение ранее изученного материала;
подведение первого тура
соревнования;
знакомство с практическим применением геометрической прогрессии;
вывод формулы Sn.
решение задач;
подведение
второго тура соревнования;домашнее задание.
Слайд 8 Числовая последовательность (отличных от нуля членов), каждый член
которой, начиная со второго больше предыдущего на одно и
то же число, называется геометрической прогрессией.
Слайд 9
Правильный ответ
Геометрической последовательностью называется последовательность отличных от нуля
чисел, каждый член которой начиная со второго, равен предыдущему
члену, умноженному на одно и то же число.
Слайд 18
Задача
Однажды незнакомец постучал в окно к богатому
купцу и предложил сделку: «Я буду ежедневно в течении
30 дней приносить тебе по 100000 р. А ты мне в 1-ый день отдашь за 100000 1коп, во 2-ой день – 2коп. И так каждый день будешь увеличивать предыдущее количество денег в 2 раза. Если тебе выгодна сделка, то завтра и начнем. Купец обрадовался такой удачи. Он подсчитал, что получит 3000000р. На следующий день они пошли к нотариусу и заверили сделку.Слайд 29 Для этого достаточно иметь формулу для вычисления суммы
